高次補正とくりこみ可能性

参考文献：Mark Srednicki. "Quantum Field Theory". Cambridge University Press. 2006.

これまでで，6次元の$\varphi^3$理論における2本，3本，4本の外部線を持つ1ループダイアグラムを計算した．その結果，最初の2つは発散する運動量積分を含んでいたが，これらの発散はLagrangian中の項の係数に吸収できることが分かった．もしこの性質が，プロパゲーターや1粒子既約頂点関数（外部線が$n\geq 3$本の場合）に対するすべての高次（$g$のべき）補正についても成り立つならば，その理論は「くりこみ可能（renormalizable）」であると言う．もしそうでなく，さらなる発散が現れる場合，それらを新たな項をLagrangianに加えることで吸収できるかもしれない．もしそのような新しい項が有限個で済むならば，やはり理論はくりこみ可能と呼ばれる．しかし，無限個の新しい項が必要になる場合，その理論は「くりこみ不可能（nonrenormalizable）」であると言う．無限個のパラメータが必要になるにもかかわらず，くりこみ不可能な理論も，ある紫外カットオフ$\Lambda$より低いエネルギーでは有用な予測を行うことが一般的に可能である．この点については後で議論する．

このセクションでは，くりこみ可能性のための必要条件を導出する．例として，$d$次元時空におけるスカラー場理論を考える．そのLagrangianは次の形で与えられる： $$ \mathcal{L}=-\frac{1}{2}Z_{\varphi}\partial^{\mu}\varphi\partial_{\mu}\varphi-\frac{1}{2}Z_mm^2\varphi^2-\sum_{n=3}^{\infty}\frac{1}{n!}Z_ng_n\varphi^n $$

外部線の本数を $E$，内部線の本数を $I$，閉じたループの数を $L$，$n$本の線をつなぐ頂点の数を $V_n$ とするFeynmanダイアグラムを考える（ここで $V_n$ は単なる数であり，頂点関数 $\bm{V}_n$ とは区別する）．このダイアグラムに対応する運動量積分は発散するだろうか？

まず，各閉じたループは $d^d\ell_i$ の因子を与え，各内部プロパゲーターは $1/(p^2 + m^2)$ の因子を与えることに注意する．ここで $p$ は外部運動量 $k_i$ やループ運動量 $\ell_i$ の線形結合である．したがって，このダイアグラムは，分子に含まれる $\ell$ の数が分母より多い場合，大きな $\ell_i$ で紫外発散を持つように見える．分子中の $\ell$ の数から分母中の $\ell$ の数を引いたものが，このダイアグラムの「表面的発散次数（superficial degree of divergence）」である． $$ D \equiv dL-2I $$ そして，ダイアグラムは $$ D \geq 0 $$ のとき発散するように見える．

次に，より有用な $D$ の式を導出する．ダイアグラムには $E$ 本の外部線があるので，すべての線が1つの頂点で結ばれる木ダイアグラムも考えられる．このとき頂点因子は $-iZ_Eg_E$ となる．実際，これはこの全体のダイアグラムの値であり，質量次元は $[g_E]$ となる（$Z$ は定義により無次元）．したがって，元のダイアグラムも同じ散乱振幅への寄与なので，質量次元は $[g_E]$ である： $$ [\text{diagram}]=[g_E] $$ 一方，任意のダイアグラムの質量次元は，その構成要素の質量次元の和で与えられる．すなわち， $$ [\text{diagram}]=dL-2I+\sum_{n=3}^{\infty}V_n[g_n] $$ 以上より $$ D=[g_E]-\sum_{n=3}^{\infty}V_n[g_n] $$ これが必要な式である．

もし任意の $[g_n] < 0$ となる場合，その種類の頂点を追加するごとに $D$ が増加し，発散が制御できなくなることが直ちに分かる．したがって，$[g_n] < 0$ となる項を含む理論はくりこみ不可能である．

次元解析の結果によれば，結合定数の質量次元は $$ [g_n]=d-\frac{1}{2}n(d-2) $$ となる．したがって， $$ [g_n]<0 \quad \text{for} \quad n > \frac{2d}{d-2} $$ となる．よって，4次元では$\varphi^4$より高次の項，6次元では$\varphi^3$より高次の項は許されないことが分かる．

同じ基準はより複雑な理論にも当てはまる．すなわち，Lagrangian中のいずれかの項の係数が負の質量次元を持つ場合，その理論はくりこみ不可能である．

では，結合定数が正またはゼロの質量次元を持つ理論はどうだろうか？発散しうる（$D \geq 0$ となる）危険なダイアグラムは $[g_E] \geq 0$ となる場合だけであることが分かる．しかしこの場合，発散は単に $Z_E$ の値を調整することで吸収できる．この議論はプロパゲーターにも当てはまる．$\Pi(k^2)$はループ補正された相殺項頂点 $Ak^2 + Bm^2$ を表していると考えられ，$A$と$Bm^2$が2つの結合定数の役割を果たす．$[A] = 0$，$[Bm^2] = 2$ なので，寄与するダイアグラムは発散することが予想される（実際に詳細に見てきた通り），そしてその発散は$A$や$Bm^2$に吸収されなければならない．

$D$は「表面的発散次数（superficial degree of divergence）」と呼ばれるが，実際には$D < 0$でもダイアグラムが発散する場合や，$D\geq 0$でも有限となる場合がある．後者は，分子中の$\ell$の間で打ち消し合いが起こる場合に生じる．量子電磁力学（QED）ではこの現象の例が現れ，後で扱う予定である．ここでは，$D < 0$にもかかわらず発散するダイアグラムの場合に注目する．

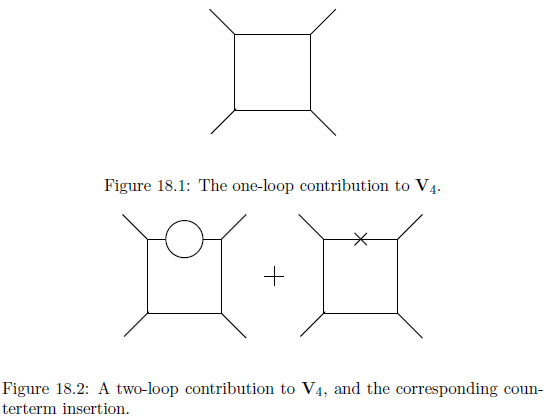
例えば，図のダイアグラムを考えよう．$E=4$の場合の図の1ループダイアグラムは有限だが，2番目の図の最初のダイアグラムによる2ループ補正では，上側プロパゲーター上のバブルが発散する．これは発散する部分ダイアグラム（サブダイアグラム）の例である．しかし，この場合は問題にならない．なぜなら，バブルの代わりに相殺項頂点を持つ図の2番目のダイアグラムによってこの発散が打ち消されるからである．

これは一般的な状況である：発散する部分ダイアグラムとは，それ単体で考えたときに $D \geq 0$ となるダイアグラムである．これらはまさに，対応するtreeダイアグラムの $Z$ 因子を調整することで発散を打ち消すことができるダイアグラムである（すべての非零 $g_n$ について $[g_n] \geq 0$ となる理論において）．

したがって，すべての結合定数の質量次元が正またはゼロである理論は，くりこみ可能であると期待される．このことを完全に証明するには，Feynmanダイアグラムに現れる運動量積分の性質を詳細に調べる必要がある．この結論は，スピン0およびスピン1/2の場のみを含む理論については，追加の制限なしに成り立つことが分かっている．

スピン1の場を含む理論が$d=4$でくりこみ可能となるのは，これらのスピン1場がゲージ対称性に対応している場合に限られる．この点については後で詳しく扱う．

スピンが1より大きい場の理論は，$d \geq 4$の場合，決してくりこみ可能にはならない．