T双対性とDブレーン

参考文献：K. Becker, M. Becker, J. Schwarz, "String Theory and M-Theory", Cambridge University Press, 2007.

弦理論は弦だけの理論ではない．さまざまな次元を持つ「ブレーン」と呼ばれるものも存在する．どのようなブレーンが存在し，それらが安定に存在するかどうかは，考える理論や真空の構成によって異なる．それを調べる道具の一つは，質量のない粒子のスペクトルである．これまでの稿では，10次元Minkowski時空におけるI型およびII型超弦理論に現れる質量のない状態のスペクトルについて説明した．特に，II型理論のR-Rセクターにはいくつかの反対称テンソルゲージ場（微分形式）が現れることが示した．これらのテンソル場は，「Dブレーン」と自然に結合する．しかし，これがDブレーンの定義的な性質というわけではない．Dブレーンの定義的な性質は，開いた弦がその端点をDブレーン上に持つことができるということである．反対称テンソルゲージ場に電荷結合を持つDブレーンは安定だが，そうでないものは通常不安定である．

Dブレーンの必要性を動機づける一つの方法は「T双対性」に基づいている．そこで，ここではまずボソン弦理論のT双対性について議論する．T双対変換の下で，閉じたボソン弦はT双対な空間における同じ型の閉じたボソン弦へと変換される．しかし，開いた弦の場合は状況が異なる．重要なのは，開いた弦の端点に課される境界条件の種類に注目することである．全ての時空方向でPoincaré不変性と両立する開いた弦の境界条件は「Neumann型」のみであるが，T双対な定式化では「Dirichlet境界条件」が必然的に現れる．特定の時空方向にDirichlet境界条件を持つ開いた弦は，その方向において弦の端点の位置が指定されていることを意味する．これはLorentz不変性を破るが，このような端点の存在には物理的な理由がある．それは，開いた弦がD$p$ブレーンの上に端を持つことに起因する．ここでDはDirichlet条件を，$p$はDブレーンの空間次元を表す．例えば，D0ブレーンは点粒子である．時間方向も考慮すると，D$p$ブレーンの世界体積は$p+1$次元となる．

D$p$ブレーンの重要性の多くは，それらが弦理論に非可換ゲージ対称性を導入する驚くべき方法を提供する点にある．非可換ゲージ場は，複数のD$p$ブレーンが重なり合った世界体積上に自然に現れる．さらに，D$p$ブレーンは，一見異なる弦理論同士を関係づける双対性を発見する上でも有用である．T双対性は摂動論的弦理論の枠組みで理解できるため，本稿で導入される．他の多くの弦の双対性は非摂動論的である．弦理論の双対性の一般的な話題については，別の稿でより詳しく議論する．

目次

• ボソン弦とD$p$ブレーン
  • T双対性と閉じた弦
  • T双対性と開いた弦
  • Chan-Paton電荷，Wilsonライン，複数のブレーン
• II型超弦理論におけるDブレーン
  • 微分形式とDブレーン電荷
  • II型超弦理論における安定なブレーン
  • 非BPSブレーン
  • II型超弦理論におけるT双対性
  • K理論
• I型超弦理論
  • orientifold射影
  • その他のI型Dブレーン
  • I'型超弦理論
• 背景場の存在下におけるT双対性
  • NS-NSセクターの場
  • R-Rセクターの場
• Dブレーンの世界体積作用

ボソン弦とD$p$ブレーン

T双対性と閉じた弦

T双対性の概念を導入するために，まず最も単純な例，すなわち25個の空間次元のうち1つが半径$R$の円となっているボソン弦を考える．全体の時空は，25次元Minkowski時空と円$S^1$の直積$\mathbb{R}^{24,1} \times S^1$である．このようなセットアップは「半径$R$の円へのコンパクト化」と呼ばれることもある．この場合，T双対変換は円の半径を$R \to \tilde{R} = \alpha'/R$と写す．また，弦の「巻き付き数」と「Kaluza-Klein励起数」を入れ替えることで，弦の質量公式を不変に保つ．これがどのように成り立つかを以下で見ていく．

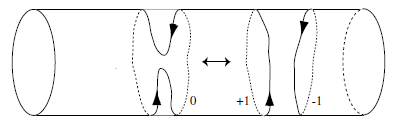
半径$R$の円でコンパクト化された理論における閉じたボソン弦を記述するには，1つの座標に対して周期的境界条件を課す必要がある： $$ X^{25}(\sigma+\pi,\tau)=X^{25}(\sigma,\tau)+2\pi RW \quad W\in\mathbb{Z} $$ ここで$W$は巻き付き数（winding number）である．$W$は弦が円に何回巻き付いているかを示し，その符号は巻き付く向きを表す．巻き付き数$W$を持つ閉じた弦のモード展開を考える．コンパクト化しない座標$X^\mu$（$\mu=0,\ldots,24$）のモード展開は，26次元Minkowski空間の場合と変わらない．しかし，コンパクト化された座標$X^{25}(\sigma,\tau)$の展開は，境界条件を満たすために$\sigma$に線形な項を加える必要がある．そのモード展開は $$ X^{25}(\sigma,\tau)=x^{25}+2\alpha'p^{25}\tau+2RW\sigma+\cdots $$ となる．ここで$\sigma$の係数は境界条件を満たすように選ばれている．「$\cdots$」は，コンパクト化によって修正を受けない既存の振動項を表す．

1つの次元がコンパクト化されているため，その方向の運動量固有値$p^{25}$は量子化される．量子力学的な波動関数には$\exp(ip^{25}x^{25})$という因子が含まれたことを思い出そう．このとき，$x^{25}$を$2\pi R$だけ増やす，すなわち円を1周すると，波動関数は元の値に戻らなければならない（波動関数の一価性）．これより，$X^{25}$方向の運動量は次の形になる： $$ p^{25} = \frac{K}{R} \quad K \in \mathbb{Z} $$ ここで$K$はKaluza-Klein励起数（Kaluza-Klein excitation number）と呼ばれる整数である．モード展開を左・右進行波に分けると， $$ X^{25}(\sigma,\tau) = X_L^{25}(\tau+\sigma) + X_R^{25}(\tau-\sigma) $$ となる．これを具体的に書くと， \begin{align*} X_R^{25}(\tau-\sigma) =& \frac{1}{2}(x^{25}-\tilde{x}^{25})+(\alpha'\frac{K}{R}-WR)(\tau-\sigma) + \cdots \\ X_L^{25}(\tau+\sigma) =& \frac{1}{2}(x^{25}+\tilde{x}^{25})+(\alpha'\frac{K}{R}+WR)(\tau+\sigma) + \cdots \end{align*} ここで$\tilde{x}^{25}$は和をとると消えるような定数である．ゼロモード$\alpha_0^{25}$と$\tilde{\alpha}_0^{25}$を用いると，モード展開は \begin{align*} X_R^{25}(\tau-\sigma) =& \frac{1}{2}(x^{25}-\tilde{x}^{25})+\sqrt{2\alpha'}\alpha_0^{25}(\tau-\sigma) + \cdots \\ X_L^{25}(\tau+\sigma) =& \frac{1}{2}(x^{25}+\tilde{x}^{25})+\sqrt{2\alpha'}\tilde{\alpha}_0^{25}(\tau+\sigma) + \cdots \end{align*} となる．ここで \begin{align}\label{6.9} \sqrt{2\alpha'}\alpha_0^{25} &= \alpha'\frac{K}{R}-WR \\ \label{6.10} \sqrt{2\alpha'}\tilde{\alpha}_0^{25} &= \alpha'\frac{K}{R}+WR \end{align} である．

1次元分が円でコンパクト化された場合の弦の質量公式は，25次元の理論の観点から解釈できる．この場合，各Kaluza-Klein励起状態（$K$でラベル付けされる状態）は異なる粒子として扱われる．25次元の理論における質量の二乗は $$ M^2=-\sum_{\mu=0}^{24}p_{\mu}p^{\mu} $$ で与えられる．一方，物理状態に対して$L_0-1$および$\tilde{L}_0-1$がゼロになるという条件は依然として成り立たなければならない．$L_0$と$\tilde{L}_0$の式には25番目の空間次元も含めた全26次元分の寄与が含まれる．その結果，$L_0=1$および$\tilde{L}_0=1$は $$ \frac{1}{2}\alpha'M^2=(\tilde{\alpha}_0^{25})^2+2N_L-2=(\alpha_0^{25})^2+2N_R-2 $$ となる．これらの式の和と差をとり，\eqref{6.9}および\eqref{6.10}式を用いると \begin{equation}\label{6.13} N_R-N_L=WK \end{equation} および \begin{equation}\label{6.14} \alpha'M^2=\alpha'\left[ \left( \frac{K}{R} \right)^2+\left( \frac{WR}{\alpha'} \right)^2 \right]+2N_L+2N_R-4 \end{equation} $$ となる．式\eqref{6.13}は，巻き付き数$W$とKaluza-Klein励起数$K$がともにゼロでない場合，通常のレベルマッチング条件$N_L=N_R$からどれだけずれるかを表している．

式\eqref{6.13}と式\eqref{6.14}は，$W$と$K$を入れ替え，かつ$R \to \tilde{R} = \alpha'/R$という変換することで不変に保たれる．このボソン弦の対称性はT双対性（T-duality）と呼ばれる．これは，半径$R$の円へのコンパクト化と半径$\tilde{R}$の円へのコンパクト化が物理的に等価であることを示唆している．実際，少なくとも摂動論的には，これは相互作用を含む完全な弦理論においても正しいことが分かっている[1]．

ここで考えた例では，T双対性は同じ型の2つの理論（半径$R$の円と半径$\tilde{R} = \alpha'/R$の円）を互いに写し合う．半径$R$の円と半径$\tilde{R}$の円が物理的に等価であるという事実は，弦理論においては通常の幾何学的概念に対する直感が弦スケールで破綻しうることを明確に示している．これは，調べる対象自体が弦スケールの大きさを持つことを考えれば，それほど驚くべきことではない．$W$と$K$の入れ替えは，一方の記述における運動量の励起状態が，双対な定式化では巻き付き数の励起状態に対応し，その逆も成り立つことを意味している．

上付き添字25を省略すると，この変換は次のように表せる： $$ \alpha_0 \to -\alpha_0 \quad \text{and} \quad \tilde{\alpha}_0 \to \tilde{\alpha}_0 $$ 変換されるのはゼロモードだけでなく，コンパクト化される座標の右進行波全体がT双対変換の下で符号反転する： $$ X_R \to -X_R \quad \text{and} \quad X_L \to X_L $$ この変換が理論の対称性であることは，エネルギー運動量テンソルや相関関数などの物理量がこの変換の下で不変であることから明らかである．同等に，$X$は次の$\tilde{X}$に写される： $$ \tilde{X}(\sigma,\tau)=X_L(\tau+\sigma)+X_R(\tau-\sigma) $$ このモード展開は $$ \tilde{X}(\sigma,\tau)=\tilde{x}+2\alpha'\frac{K}{R}\sigma+2RW\tau+\cdots $$ ここで，元の円の周期$2\pi R$でパラメータ化されていた座標$x$が，$\tilde{x}$という新しい座標に置き換えられていることに注意しよう．この$\tilde{x}$は双対円の周期$2\pi\tilde{R}$でパラメータ化されている．なぜなら，その共役運動量は$\tilde{p}_{25}=RW/\alpha'=W/\tilde{R}$となるからである．

T双対性とシグマ模型

T双対性が$X(\sigma, \tau)$と$\bar{X}(\sigma, \tau)$を入れ替えるという結論は，世界面の作用の観点からも理解できる．次の世界面作用を考えよう： $$ \int \left( \frac{1}{2}V^{\alpha}V_{\alpha} - \varepsilon^{\alpha\beta}X\partial_{\beta}V_{\alpha} \right) d^2\sigma $$ ここで全体の定数係数は省略している．この省略は以降の議論が古典的なので問題ない．$X$について変分をとると，$X$はLagrange乗数として働き，運動方程式$\varepsilon^{\alpha\beta}\partial^{\beta}V_{\alpha} = 0$が得られる．これは$V_{\alpha} = \partial_{\alpha}\tilde{X}$と置くと解ける（ここで$\tilde{X}$は任意の関数である）．これを作用に代入すれば自由なボソン場$\tilde{X}$の作用 $$ \frac{1}{2}\int \partial^{\alpha}\tilde{X}\partial_{\alpha}\tilde{X} d^2\sigma $$ となる．一方，元の作用を$V_{\alpha}$で変分すると，運動方程式$V_{\alpha} = -\varepsilon_{\alpha}{}^{\beta}\partial_{\beta}X$が得られる．これを作用に代入し，次の関係式 $$ \varepsilon^{\alpha\beta}\varepsilon_{\alpha}{}^{\gamma} = -\eta^{\beta\gamma} $$ を使うと，自由なボソン場$X$の作用 $$ \frac{1}{2}\int \partial^{\alpha}X\partial_{\alpha}X d^2\sigma $$ となる．両者の$V_{\alpha}$の式を比較すると $$ \partial_{\alpha}\bar{X} = -\varepsilon_{\alpha}{}^{\beta}\partial_{\beta}X $$ となり，これはT双対変換と等価である．このような世界面の作用によるT双対性の解析は，後で背景場を含むより一般的な場合にも繰り返される．トーラスへの一般化については次稿で議論する．

T双対性と開いた弦

境界条件

26次元Minkowski時空におけるボソン弦のダイナミクスは，共形ゲージで次の作用によって記述される： $$ S=-\frac{1}{4\pi\alpha'}\int d\tau d\sigma \eta^{\alpha\beta}\partial_{\alpha}X^{\mu}\partial_{\beta}X_{\mu} $$ 変分$\delta X$に対する作用の変分は，運動方程式を与える体積項と，境界項からなる： $$ \delta S = -\frac{1}{2\pi\alpha'}\int d\tau \partial_{\sigma}X_{\mu}\delta X^{\mu}|_{\sigma=0}^{\sigma=\pi} $$ 以前述べたように，この境界項を消すためには，開いた弦の端点に適切な境界条件を課す必要がある． すべての26次元でPoincaré変換の不変性と両立する唯一の境界条件の選択は，$X$の全成分に対するNeumann境界条件である： $$ \frac{\partial}{\partial\sigma}X^{\mu}(\sigma,\tau)=0 \quad \text{for} \quad \sigma=0,\pi $$ ここで自然な問いとして，開いた弦を含む理論にT双対変換を適用すると何が起こるかがある．円でコンパクト化された理論における開いた弦について最初に注意すべき点は，開いた弦には巻き付きモードが存在しない点である．位相的に，開弦は常に1点に収縮できるため，巻き付き数という概念は意味を持たない．巻き付き数は，T双対性によって2つのボソン弦理論の閉じた弦のスペクトルを関係づける上で重要だったため，そもそも巻き付き数がill-definedな開いた弦が同じように変換されるとは期待できない．この点について，もう少し詳しく見る．

Neumann境界条件を持つ開いた弦のT双対変換を求めるために，前の稿で見たように，Neumann境界条件を持つ開いた弦の時空座標のモード展開 $$ X(\tau,\sigma)=x+p\tau+i\sum_{n\neq0}\frac{1}{n}\alpha_n e^{-in\tau} \cos(n\sigma) $$ を考える．ここで，$l_s=1$すなわち$\alpha_0'=1/2$とした．閉じた弦の場合と同様に，モード展開を左・右進行波に分けると便利である．これらの展開は \begin{align*} X_R(\tau-\sigma) =& \frac{x-\tilde{x}}{2}+\frac{1}{2}p(\tau-\sigma)+\frac{i}{2}\sum_{n\neq0}\frac{1}{n}\alpha_n e^{-in(\tau-\sigma)} \\ X_L(\tau+\sigma) =& \frac{x+\tilde{x}}{2}+\frac{1}{2}p(\tau+\sigma)+\frac{i}{2}\sum_{n\neq0}\frac{1}{n}\alpha_n e^{-in(\tau+\sigma)} \end{align*} となる．

再び半径$R$の円でコンパクト化し，T双対変換を行うと， \begin{equation}\label{6.27} X_R \to -X_R \quad \text{and} \quad X_L \to X_L \end{equation} となる．コンパクト化された25番目の空間方向の双対座標は， \begin{equation}\label{6.31} \tilde{X}(\tau,\sigma)=X_L-X_R=\tilde{x}+p\sigma+\sum_{n\neq0}\frac{1}{n}\alpha_n e^{-in\tau} \sin(n\sigma) \end{equation} となる．ここで，T双対理論の性質を読み取ろう．まず，双対な理論の開いた弦はコンパクト化された25番目の空間方向に運動量を持たない．なぜなら，上式には$\tau$に線形な項が含まれていないからである（$\tau$で微分しても何も出てこない）．したがって，双対な開いた弦の座標は振動運動のみを行うことが分かる．次に，式\eqref{6.31}から，双対な開いた弦がコンパクト化された時空方向で満たすべき境界条件を読み取ることができる．$\sigma=0,\pi$では$\sin$による振動子項が消えるため，弦の端点の位置は固定される．これは，T双対変換によってNeumann境界条件がDirichlet境界条件に写されたことを意味する．実際，元の場\eqref{6.27}と双対変換された場\eqref{6.27}を比較すれば分かる．境界条件を明示的に書けば $$ \tilde{X}(\tau,0)=\tilde{x} \quad \text{and} \quad \tilde{X}(\tau,\pi)=\tilde{x}+\frac{\pi K}{R}=\tilde{x}+2\pi K\tilde{R} $$ となる．ここで$p=K/R$および双対な半径$\tilde{R}=\alpha'/R$を用いた．この端が固定された弦は双対な円を$K$回巻いていることに注意する．この巻き付きモードはトポロジー的にwell-definedであり，弦の端点がDirichlet境界条件によって固定されているため，弦を切断しない限りほどけることはない．

Dブレーン

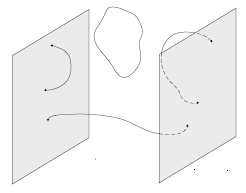
T双対性は，半径$R$の円上でNeumann境界条件を持つ開いたボソン弦を，半径$\tilde{R}$の円上でDirichlet境界条件を持つ開いたボソン弦へと変換した．もともと円方向に運動量を持ち巻き付いていなかった弦が，双対な円方向では巻き付いてはいるが運動量は持たない弦へと変化した．双対な開いた弦の端点は超平面$\tilde{X} = \tilde{x}$に固定されており，円を整数回巻くことができる．この超平面$\tilde{X} = \tilde{x}$がDirichletブレーン，略してDブレーン（D-brane）の例である．一般に，Dブレーンとは開弦の端点が端を持つことができる超曲面として定義される（下図参照）．重要なのは，これは単なる空間上の任意の位置ではなく，物理的な対象であるという点である．通常，ブレーンの次元を指定してD$p$ブレーンと呼び，$p$はその空間次元数を表す．この例では$p=24$のD24ブレーンである．すべての方向でNeumann境界条件を持つ開いたボソン弦にT双対変換を適用すると，双対な理論では対応する開いた弦が双対な円方向にDirichlet境界条件を持ち，D24ブレーン上に端を持つことが分かる．

この議論は，他の方向も円として取り，各方向でT双対変換を施すことで繰り返すことができる．$n$個の円（すなわち$n$次元トーラス）から始めると，T双対な定式化では開した弦が$n$個の時空方向でDirichlet境界条件を持つことになる．これは，弦がD$(25-n)$ブレーン上に端を持つことを意味する．では，元の記述における開いた弦（つまり，すべての方向でNeumann境界条件を持つ）はどうなるだろうか．これは明らかに$n=0$の場合なので，これらの開いた弦は時空を満たすD25ブレーン上に端を持つとみなせる．一般に，さまざまな次元のDブレーンが複数存在する状況を考えることができる．T双対な定式化では，それらは他の次元のDブレーンに置き換わる．

要約すると，前述の議論から得られる一般的な規則は，DブレーンがT双対変換を受ける円を巻いている場合，双対な理論ではその円を巻かず，逆もまた然りであるということである．

開いた弦のタキオン状態

ボソン弦理論の重要な特徴の一つは，スペクトルにタキオン状態が存在することである．以前見たように，これは閉じた弦のスペクトルにも開いた弦のスペクトルにも当てはまる．また，いくつかの時空方向でDirichlet境界条件を満たす開した弦についても同様である．

タキオン状態は場の子論的な不安定性を表すと解釈できる．$M^2$が負であることは，場の空間において有効ポテンシャルが極大値または鞍点にあることを示している．ここで疑問となるのは，「真の真空はどこか？」ということである．開いた弦のタキオン状態の場合，対応するD$p$ブレーンは閉じた弦の放射へと崩壊すると考えられている．したがって，弦との結合がオンになると，ボソン弦理論には安定な対象としてDブレーンおよび開いた弦は実際には含まれないことが分かる．結合が非常に小さくない限り，これらのDブレーンは急速に崩壊することが知られている．この描像は，Wittenの開いた弦の場の理論による詳細な計算によって裏付けられている．この基本的なアイデアは，エネルギー密度を最小化する弦の場の構成を見つけ，不安定なタキオン真空状態に対するエネルギー差が時空を満たすDブレーンのエネルギー密度（または張力）に等しいことを示すことである．「レベル消去（level-truncation）」と呼ばれる近似手法を用いることで，1\%未満の精度で一致が得られている．

Chan-Paton電荷，Wilsonライン，複数のブレーン

前節の構成では，Neumann境界条件を持つ開いた弦にT双対性を適用することで，自然に単一のD$p$ブレーンが現れた．この節では，単一ではなく複数のD$p$ブレーンが存在する場合，非常に興味深い現象が起こることを示す．すなわち，理論に非可換ゲージ対称性が現れる．

開いた弦の端点には，Chan-Paton電荷と呼ばれる追加の自由度を持たせることができる．これらの自由度は，弦理論が強い相互作用のモデルとして発展していた当初，開いた弦の端に付随するクォークや反クォークのフレーバー量子数を記述するために導入されたものである．元々は，弦の端に位置するクォーク・反クォーク対に作用する大域的な$SU(2)$アイソスピン対称性を記述することが目的だったが，最終的にはこの構成がゲージ対称性を与えることが明らかとなっていった．

Chan-Paton因子は，弦の各端点に$N$個の自由度を付与するものである．これまで議論してきた向き付けられた開いた弦の場合，弦の両端は区別されるため，$\sigma=0$端には基本（定義）表現$\bm{N}$，$\sigma=\pi$端には反基本表現$\bar{\bm{N}}$を割り当てることができる．このようにして，ゲージ群$U(N)$が記述される．

I型超弦理論のような向き付けられていない弦の場合，両端に割り当てられる表現は同じでなければならず，これにより対称性を記述する群は基本表現が実であるもの，すなわち直交群またはシンプレクティック群に限られる．各状態は，向きの反転（両端を入れ替える操作）に対して対称または反対称となる．もし質量のないベクトル状態が反対称な状態に対応するなら，その数は$N(N-1)/2$であり，群は$SO(N)$となる．一方，対称な場合は$N(N+1)/2$となり，群は$USp(N)$となる．シンプレクティック行列は偶数次元のみ存在するため，後者の群は$N$が偶数の場合にのみ存在する．

向き付けられた開いたボソン弦の場合を考えよう．この場合，開いた弦のスペクトルの各状態には追加で$N^2$の縮退度を持つ．特に，$N^2$個の質量のないベクトル状態は$U(N)$ゲージ場を記述する（電磁場と同様）．弦の端に付随する電荷は残るゲージ対称性に対応しているため保存される．また，エネルギー運動量テンソルは新しい自由度に依存しないので，理論の共形不変性は影響を受けない．一般に，Chan-Paton電荷は世界面理論では動的ではなく，下図のような散乱過程において各世界面の境界に一意な添字が割り当てられる．この図の三点散乱振幅（他の開いた弦の振幅も同様）は，Chan-Paton行列に由来する追加因子 $$ \delta^{ii'}\delta^{jj'}\delta^{kk'}\lambda_{ij}^1\lambda_{j'k}^2\lambda_{k'i'}^3=\mathrm{Tr}\lambda^1\lambda^2\lambda^3 $$ を含む．$\lambda$行列は弦の電荷状態をエンコードする．世界面の内部の境界については，対応するChan-Paton添字で和をとる必要があり，これにより$N$の因子が得られる．これによって散乱振幅が$U(N)$対称性の下で不変となることが保証される．

開いた弦の状態空間の基底は，通常のFock空間状態，つまり運動量$k$，そして弦の左端と右端に対応するChan-Paton電荷を表す整数$i, j = 1, 2, \ldots, N$でラベル付けできる： $$ |\phi, k, ij \rangle $$ この状態は$U(1)_i$の下で電荷$+1$，$U(1)_j$の下で電荷$-1$で変換される．任意の弦の状態を記述するには，$U(N)$代数の表現行列である$N^2$個のエルミート行列，すなわちChan-Paton行列$\lambda_{ij}$を導入する必要がある．任意の状態は次のような線形結合で表せる： $$ |\phi, k, \lambda \rangle = \sum_{i,j=1}^{N} |\phi, k, ij \rangle \lambda_{ij} $$ 弦の状態は$U(N)$の随伴表現で変換される行列となる．これにより，$N^2$個のタキオン，$N^2$個の質量のないベクトルボソンなどが現れる．

円でコンパクト化された理論では，平坦なポテンシャル[2]はAharanov-Bohm効果に類似した非自明な物理効果を持つことがある．ゲージポテンシャルの円方向の成分がゼロでない定数値を取る場合，これはホロノミー行列，すなわちWilsonラインを与える： $$ U = \exp\left(i \int_0^{2\pi R} A dx\right) $$ エルミート行列$A$をゲージ変換を使って対角化すると，次の形に書ける： $$ A = -\frac{1}{2\pi R} \mathrm{diag}(\theta_1, \theta_2, \ldots, \theta_N) $$ Wilsonラインで特徴づけられるゼロでないゲージ場の存在は，$U(N)$ゲージ対称性を$U$と可換な部分群へと自発的に破る．例えば，$U$の固有値がすべて異なる場合，対称性は$U(N)$から$U(1)^N$へと破れる．

Wilsonラインが存在する場合，弦の状態$|\phi, k, ij\rangle$に割り当てられる運動量はシフトされ，波動関数は $$ e^{ip2\pi R}=e^{-i(\theta_i-\theta_j)} $$ となる．したがって，円方向の運動量は分数値となり， \begin{equation}\label{6.39} p=\frac{K}{R}-\frac{\theta_i-\theta_j}{2\pi R} \quad K \in \mathbb{Z} \end{equation} となる．T双対変換を適用すると，$\theta_i$は双対な円上の$N$個のD24ブレーンの角度を表すことが分かる．実際，運動量の励起数は巻き付き数に写されるため，Wilsonラインによって導入された分数のKaluza-Klein励起数は分数の巻き付き数に写される．ここで分数の巻き付き数とは，開いた弦が円の一部分だけ巻いていることを意味する．$\theta_i = \theta_j$ の場合のみ，巻き付き数は整数となる．

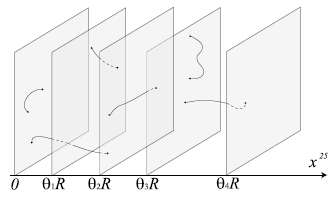
双対な開いた$ij$弦のモード展開は $$ \tilde{X}_{ij}^{25} = \tilde{x}_0 + \theta_i \tilde{R} + 2\tilde{R}\sigma \left( K + \frac{\theta_j - \theta_i}{2\pi} \right) + \cdots $$ となるので，一方の端点は$\tilde{x}_0 + \theta_i \tilde{R}$に，もう一方の端点は$\tilde{x}_0 + \theta_j \tilde{R}$に位置することになる．これは，$\sigma = 0$の端点が$i$番目のDブレーンに，$\sigma = \pi$の端点が$j$番目のDブレーンにある開いた弦として解釈できる．対角成分iiに対応する弦は円を整数回巻くが，非対角成分ijに対応する弦は一般に整数回を巻かないことに注意する．

スペクトル

円でコンパクト化されたボソン弦理論における開いた$ij$弦のスペクトルは \begin{equation}\label{6.41} M_{ij}^2 = \left( \frac{K}{R} + \frac{\theta_j - \theta_i}{2\pi R} \right)^2 + \frac{1}{\alpha'}(N - 1) \end{equation} で与えられる[3]．この式は，質量殻条件と$p^{25}$成分の運動量が式\eqref{6.39}に従ってシフトされることから導かれる．

式\eqref{6.41}から，すべての$\theta_i$が異なる場合，質量のないベクトル状態は円を巻かず，同じDブレーンの上で始まり終わる弦からのみ生じることが分かる．他のベクトル状態はすべて質量を持つ．したがって，Dブレーンが重なっていない場合，$K=0$の対角成分の弦によって$N$個の異なる質量のない$U(1)$ベクトル状態が得られる．結果として，残るゲージ対称性は$U(1)^N$となる．

もし2つの$\theta_i$が等しく，2つのDブレーンが重なっている場合，2つの非対角成分の弦の状態が質量ゼロとなる．このとき，ゲージ対称性は$U(1) \times U(1)$から$U(2)$へと「強化（enhance）」される．Dブレーンが分離すると，ゲージ対称性は$U(1) \times U(1)$に破れ，非対角成分の非可換ゲージボソンは弦的なHiggs機構によって質量を持つようになる．より一般的には，$N_0 \leq N$個のDブレーンが重なると，残るゲージ対称性は$U(N_0)$を含むことになる．したがって，複数のDブレーンが重なることで，弦理論において非可換ゲージ対称性を実現することができる．この事実は非常に重要である．例えば，下図のように5枚の平行なDブレーンが集まると，$U(1)^5$のゲージ対称性が得られる．

いくつかの状態の具体的な形をより詳しく見てみよう．質量のない状態は，一般に1点に収縮できる開いた弦から生じる．これらの弦は同じDブレーン（または重なったDブレーン）上で始まって終わり，その世界体積上に存在するとみなされる．具体的には，スペクトルに現れる質量のない状態の一つは，円方向の振動子励起に由来するスカラー粒子である： $$ \alpha_{-1}^{25}|0,k\rangle $$ これはスカラー場$A_{25}(\vec{x})$に対応する．他の成分はD24ブレーンに接する方向であり， $$ \alpha_{-1}^{\mu}|0,k\rangle \quad \mu = 0,1,\ldots,24 $$ これらはベクトル場$A_\mu(\vec{x})$に対応する．ここで$\vec{x} = (x^0, \ldots, x^{24})$はD$p$ブレーン上の座標を表す．これらは円の座標$x^{25}$以外の25個の座標であり，$x^{25}$はDブレーンの位置に固定されている．したがって，これらの状態はD24ブレーン上のゲージ場を記述する．

$A_{25}$が25個のコンパクトでない時空座標に依存することを許すと，D24ブレーンの$\tilde{x}^{25}$方向への横方向変位が世界体積上で変化し得る．したがって，$A_{25}$背景は曲がったD24ブレーン世界体積を記述することができる．より一般的には，平坦で剛体なD$p$ブレーンから出発した場合，横方向の変形は，質量のない開いた弦のスカラー状態に対応する$25-p$個の世界体積上のスカラー場の値によって記述される．これらのスカラー場は高次元ゲージ場の$25-p$個の横方向成分であり，その値がDブレーンの横方向位置を表す．Dブレーン世界体積上のこれらのスカラー場は，横方向の並進対称性が自発的に破れることに伴うGoldstoneボソンとして解釈できる．並進対称性はDブレーンの存在によって破れる．

この議論は，質量のない弦モードの凝縮（または真空期待値）が幾何学的な解釈を持つことを示している．重力の場合も同様の状況がある．弦理論を平坦時空上で定義すると，閉じた弦のスペクトルに質量のない重力子が現れ，対応する場は時空の計量となる．計量はLorentz計量と異なる値を取ることができ，それによって曲がった時空を記述する．Dブレーンの場合との重要な違いは，その時空が開いた弦のスカラー場によって制御される点である．

II型超弦理論におけるDブレーン

Dブレーンは超弦理論にも存在する．実際，ボソン弦理論の場合と同様に，IIA型やIIB型の真空構成にDブレーンを加えることで，体積には閉じた弦が存在し，Dブレーン上には端点を持つ開いた弦が現れる理論となる．超弦理論における特定のDブレーンは，ボソン弦理論には現れない重要な特徴を持つ．すなわち，保存される電荷を持ち，それによってDブレーンの安定性が保証される．この場合，Dブレーン上で始まって終わる開いた弦のスペクトルにはタキオンが存在しない．

Dブレーンが存在すると，超弦理論の真空が持ついくつかの対称性が破れる．例えば，II型超弦理論のMinkowski空間真空（10次元のPoincaré不変性を持つ）を考え，平坦なD$p$ブレーンを加え，その重力的なバックリアクション（背景時空に与える影響）を無視すると，10次元の$SO(1,9)$Lorentz対称性は$SO(1,p)\times SO(9-p)$に破れる．さらに，D$p$ブレーンの追加によって，超対称性も部分的または完全に破れる場合がある．

10次元Minkowski真空におけるII型超弦理論は，いずれも$\mathcal{N}=2$超対称性を持つことを思い出そう．各超電荷は16個の実成分を持つMajorana-Weylスピノルに対応するため，保存される超電荷は合計32個存在する．しかし，Dブレーンを含む真空で残る超対称性の最大数は16個である．これにはいくつかの理由があるが，簡単な説明として，質量のない開いた弦の状態がベクトル超多重項を形成し，このような超多重項は保存される超電荷が16個以下の場合にのみ存在することが挙げられる．したがって，II型超弦理論の真空にDブレーンを加えると，横方向の並進対称性が破れるだけでなく，元々の32個の超対称性のうち少なくとも16個が破れることになる．

微分形式とDブレーン電荷

5つの超弦理論とM理論には，さまざまな質量のない反対称テンソルゲージ場が含まれており，これらは微分形式として表すことができる．$n$形式ゲージ場は次のように与えられる： $$ A_n=\frac{1}{n!}A_{\mu_1\mu_2\cdots\mu_n}dx^{\mu_1}\wedge dx^{\mu_2}\wedge\cdots\wedge dx^{\mu_n} $$ これらは通常のMaxwell場（$n=1$の場合）の一般化とみなすことができる．この観点から，$(n+1)$形式の場の強さを$F_{n+1}=dA_n$と定義する．具体的には， $$ F_{n+1}=\frac{1}{(n+1)!}F_{\mu_1\mu_2\cdots\mu_{n+1}}dx^{\mu_1}\wedge dx^{\mu_2}\wedge\cdots\wedge dx^{\mu_{n+1}} $$ このような場の強さは，$\delta A_n = d\Lambda_{n-1}$のようなゲージ変換の下で不変である．これは外微分の2乗が常にゼロ（$d^2=0$）であることによる．

Maxwell理論

古典的な電磁気学はMaxwell方程式によって記述される．これは，電荷や電流が存在しない場合， $$ dF=0, \quad d\star F=0 $$ の形で書くことができる．ここで$F$は電場と磁場を記述する2形式（場の強さ）である．上記の方程式は，$F$と$\star F$を入れ替えても対称であることに注意する．

より一般的には，電荷と磁荷の両方を含める必要がある．電気的に帯電した粒子（電気モノポール）は存在するが，磁気モノポールはまだ観測されていない．おそらく，磁気モノポールは実験的に探査された範囲よりもはるかに大きな質量を持つと考えられている．これらを含めると，Maxwell方程式は次のようになる： $$ dF=\star J_m \quad \text{and} \quad d\star F=\star J_e $$ ここで，$J = J_\mu dx^\mu$は電流と電荷密度に関連する1形式であり， $$ J_{\mu}=(\rho,\vec{j}) $$ である．ここで$\mu = 0, \ldots, 3$は4次元の場合の添字である．点状の電荷の場合，電荷密度はデルタ関数$\rho = e\delta^{(3)}(\vec{r})$で記述され，$e$は電気的な電荷を表す．同様に，点状の磁荷には対応する「電荷」があり，これを$g$で表す．これらの電荷は，場の強さを用いて次のように定義できる： $$ e=\int_{S^2}\star F \quad \text{and} \quad g=\int_{S^2}F $$ ここで，積分は電荷を囲む2次元球面上で行われる．

電荷と磁荷は独立ではない．実際，Diracが1931年に指摘したように，磁気モノポールの場の中を運動する電気的に帯電した粒子の波動関数が一意に定義されるためには，電荷$e$と磁荷$g$がDiracの量子化条件によって関係づけられている必要がある[4]： $$ e\cdot g \in 2\pi\mathbb{Z} $$

$p$ブレーンへの一般化

以上の議論は，$D$次元において$(p+1)$形式ゲージ場と結合する$p$ブレーン（Dirichlet条件のためとは限らないブレーン）にも一般化できる．$p$ブレーンの安定性を調べるには，それらが持ちうる保存される電荷の種類を考察することが有益である．これは，点粒子（0ブレーン）が1形式ゲージ場（すなわちMaxwell場$A = A_\mu dx^\mu$）のソースとなるような電荷を持つという事実の一般化である．ここには2つの側面がある．ひとつは，電荷を持つ粒子がゲージ場と次のような相互作用で結合することである： $$ S_{\text{int}}=e\int A=e\int d\tau A_{\mu} \frac{dx^{\mu}}{d\tau} $$ ここで$e$は電荷である．もうひとつの側面は，粒子の電荷がGaussの法則によって決定されることである．これは，粒子を2次元球面で囲み，その球面上で電場を積分することに相当する．場の強度を通常通り$F = dA$と定義すると，関連する積分は $$ \int_{S^2} \star F $$ となる．$F$は2形式であり，$D$次元ではそのHodge双対$\star F$は$(D-2)$形式となる．成分で書くと $$ (\star F)^{\mu_1\mu_2\cdots\mu_{D-2}}=\frac{\varepsilon^{\mu_1\mu_2\cdots\mu_D}}{2\sqrt{-g}}F_{\mu_{D-1}\mu_D} $$ である．一般に，$D$次元Lorentz時空では$(D-2)$次元球面が点を囲むことができる．例えば，IIA型超弦理論の電気的に帯電したD0ブレーンは8次元球面$S^8$で囲むことができる．電気的に帯電した点粒子の電磁双対は，磁気的な電荷を持ち，その電荷は粒子を囲む球面上で磁場のフラックスを積分することで測定される．これは単に $$ \int F $$ であり，Maxwell場の場合は2次元積分となる．$D$次元では，2次元球面$S^2$は$(D-4)$ブレーンを囲むことができる．4次元ではこれは点粒子だが，10次元IIA型理論ではD0ブレーンの電磁双対はD6ブレーンとなる．

上記の議論は，$n$形式ゲージ場$A_n$とその場の強さ$(n+1)$形式$F_{n+1} = dA_n$に一般化できる．$n$形式ゲージ場は，世界体積が$n = p+1$次元のブレーンと電気的に結合することができる： $$ S_{\text{int}} = \mu_p \int A_{p+1} $$ ここで$\mu_p$は$p$ブレーンの電荷であり，体積からブレーンへの引き戻しが暗黙的に含まれている．すなわち， $$ \int A_{p+1} = \frac{1}{(p+1)!} \int A_{\mu_1\cdots\mu_{p+1}} \frac{\partial x^{\mu_1}}{\partial \sigma^0} \cdots \frac{\partial x^{\mu_{p+1}}}{\partial \sigma^p} d^{p+1}\sigma $$ である．これは$p=0$および$e=\mu_0$の場合の式の一般化である．このブレーンが電気的に帯電していることは，Gaussの法則$\mu_p = \int \star F_{p+2}$を用いて電荷を評価することで分かる．$D$次元では，これは$p$-ブレーンを囲むのに必要な次元である球面$S^{D-p-2}$上の積分となる．電磁双対のブレーンの電荷は，周囲の$S^{p+2}$上で$F_{p+2}$のフラックスを積分することで測定できる．$D$次元では，$S^{p+2}$は$(D-p-4)$ブレーンを囲むことができる．したがって，10次元の場合，$p$ブレーンの電磁双対は$(6-p)$ブレーンとなる．

$D=4$次元における点電荷のDirac量子化条件（$eg = 2\pi n$）は，双対な$p$ブレーン対が持つ電荷にも素直に一般化できる．本稿の規約では，10次元の場合， $$ \mu_p\mu_{6-p}\in 2\pi\mathbb{Z} $$ となる．これは，通常の証明を一般化することで導かれる．基本的なアイデアは，電気的なブレーンの波動関数が磁気的なブレーンの場の中で一意に定義されることを要求することである．すべての超弦理論およびM理論の例では，単一の$p$ブレーンは許される最小の電荷量を持つことが分かっている．つまり，単一の$p$ブレーンと単一の双対$(6-p)$ブレーンの電荷の積は正確に$2\pi$となる．

II型超弦理論における安定なブレーン

10次元の場合に特化すると，前述の議論から，$n$形式ゲージ場は$p = n-1$の$p$ブレーンと電気的に結合し，$p = 7-n$の$p$ブレーンと磁気的に結合できることが分かる．IIA型超弦理論のR-Rセクターには$n = 1$および$n = 3$のゲージ場が含まれているため，この理論には対応する電荷を持つ安定なブレーンが存在するはずである．これらは$p = 0, 2, 4, 6$のD$p$ブレーンである．偶数次元が現れるので，$p = 8$も自然に考えられるが，ブレーンの次元が時空の次元を超えることはできないので，より大きな偶数値は不可能である．D8ブレーンの存在は，10次元の場の強度を持つ9形式ゲージ場が必要となるように思える．このような場は動的ではないため，IIA型超重力理論の物理的自由度を解析した際には現れなかった．実際，安定なD8ブレーンは特別な状況下で現れるが，これについては後で別の稿で詳しく説明する．

IIB型超弦理論の場合，R-Rセクターには$n=0, 2, 4$の$n$形式ゲージ場が含まれている．上記の規則を適用すると，0形式は電気的に$(-1)$ブレーンと結合するはずである．これは空間方向だけでなく時間方向にも局在した対象であり，Dインスタントンとして解釈される（Euclid化した理論で意味を持つ）．その電磁双対はD7ブレーンであり，Lorentz符号を持つ理論でも定義できる．ただし，D7ブレーンは余次元が2なので，幾何学的には3次元一般相対論の質点と同様に欠損角を生じる．2形式は電気的にD1ブレーン（D弦とも呼ばれる）と結合し，磁気的にD5ブレーンと結合する．4形式は電気的にも磁気的にもD3ブレーンと結合する．ただし，これらは異なるDブレーンではなく，場の強さが自己双対（$F_5 = \star F_5$）であるため，D3ブレーンは自己双対な電荷を持つ．また，IIB型超弦理論では時空を満たすD9ブレーンも導入できるが，存在には整合性条件がある．まとめると，IIB型超弦理論には保存される電荷を持つ安定なD$p$ブレーンが存在し，$p$が奇数の場合に許される．

安定なDブレーン（IIA型超弦理論では$p$が偶数，IIB型超弦理論では$p$が奇数）は，超対称性の半分（16個の超対称性）を保存する．そのため，これらは「半BPS Dブレーン」と呼ばれることもある．この事実は，対応する開いた弦のスペクトルがこれだけの超対称性を持ち，したがってタキオン状態が存在しないことを意味する．具体的には，$Q_1$と$Q_2$を弦理論の2つの超対称性電荷とする．これらはMajorana-Weylスピノルであり，IIA型の場合は互いに逆のカイラリティ，IIB型の場合は同じカイラリティを持つ．今，D$p$ブレーンが方向$0,1,\ldots,p$に沿って広がっていると仮定する．このとき，保存される超対称性は次の線形結合で与えられる： $$ Q = Q_1 + \Gamma^{01\cdots p} Q_2 $$ ここで，2項目の符号は規約によって異なる．いずれの場合も，2つの項は同じカイラリティを持つことに注意する．なぜなら，Dirac行列は$p$が偶数（IIA型の場合）では$Q_2$項のカイラリティを反転させ，$p$が奇数（IIB型の場合）では反転しないからである．

要約すると，保存されるR-R電荷，超対称性，安定性，そしてタキオン状態の不在は，これらII型超弦理論のD$p$ブレーンの特徴である．

非BPS Dブレーン

タイプII超弦理論にも「間違った」$p$値（すなわちIIA型超弦理論では$p$が奇数，IIB理論では$p$が偶数）のD$p$ブレーンが存在する．これらのD$p$ブレーンは保存される電荷を持たず，不安定である．全ての超対称性を破り，開いた弦のスペクトルにはタキオン状態が含まれる．これらのブレーンの特徴は，ボソン弦理論における任意の$p$値のD$p$ブレーンと同じである．超弦理論の文脈では，この種のDブレーンは非BPS Dブレーンと呼ばれることがある．

II型超弦理論におけるT双対性

半径$R$の円でコンパクト化された閉じたボソン弦理論に対するT双対性は，理論を双対な円（半径$\tilde{R} = \alpha'/R$）上の同一の理論へと写す．この意味で，理論はT双対変換の下で自己双対であり，自己双対半径$R_{sd} = \sqrt{\alpha'}$では $\mathbb{Z}_2$対称性が存在する．次に，同じT双対変換をII型超弦理論について調べてみよう．すると，IIA型超弦理論はIIB型超弦理論へ，IIB型超弦理論はIIA型超弦理論へと写されることが分かる．もちろん，複数の方向が円でコンパクト化されている場合は，複数回のT双対変換を施すことができる．この場合，偶数回の変換では出発点と同じII型超弦理論（双対なトーラス上）に戻る．トーラスが自己双対の場合，双対性は対称性となる．

単一の円の場合に戻り，II型超弦理論の$X^9$座標が半径$R$の円でコンパクト化され，この座標に対してT双対変換が施される状況を考えよう．ボソン座標の変換はボソン弦の場合と同じであり， $$ X_L^9 \to X_L^9 \quad \text{and} \quad X_R^9 \to -X_R^9 $$ となり，運動量励起数と巻き付き数が入れ替わる．RNS形式では，世界面超対称性により，世界面フェルミオン$\psi^9$もそのボソンパートナー$X^9$と同様に変換される必要がある．すなわち， $$ \psi_L^9 \to \psi_L^9 \quad \text{and} \quad \psi_R^9 \to -\psi_R^9 $$ これにより，T双対変換後には右向きRamondセクター基底状態のカイラリティが反転する．左向きと右向き基底状態の相対的なカイラリティが，IIA型超弦理論とIIB型超弦理論を区別する要素である．片方のみが反転するため，IIA型超弦理論が半径$R$の円でコンパクト化されている場合，T双対変換を施すと，半径$\tilde{R}$の円上のIIB型超弦理論が得られることになる．

光円錐定式化では，独立した動的自由度は$X^i$のみであり，$i = 1, \ldots, 8$である．この場合，これらの方向のいずれかに沿ったT双対変換は前述の通りに作用するが，$x^9$方向に沿ったT双対変換は定式化がやや煩雑になる．

では，II型超弦理論のD$p$ブレーンがT双対変換されたときに何が起こるかを調べてみよう．IIA型超弦理論の半BPS D$p$ブレーンは$p$が偶数，IIB型超弦理論の半BPS D$p$ブレーンは$p$が奇数であるため，これらのDブレーンはT双対変換によって互いに写し合わされる．同様のことは非BPS D$p$ブレーンについても言える．この場合の解析はボソン弦の場合と同じである．ここでは，$x^\mu$（$\mu=0,\ldots,p$）方向に広がり，他の横方向の座標に定まった値を持つ2枚の平行なD$p$ブレーンのペアについて解析を復習しよう．これら2枚のD$p$ブレーンを結ぶ開いた弦は，$p+1$次元においてNeumann境界条件を満たす： $$ \partial_{\sigma}X^{\mu}|_{\sigma=0}=\partial_{\sigma}X^{\mu}|_{\sigma=\pi}=0 \quad \mu = 0,1,\ldots,p $$ また，横方向座標についてはDirichlet境界条件を満たす： $$ X^i|_{\sigma=0}=d_1^i, \quad \text{and} \quad X^i|_{\sigma=\pi}=d_2^i, \quad i = p + 1, \ldots, 9 $$ ここで$d_1^i$と$d_2^i$は定数である．これらの境界条件から，モード展開は次のようになる： \begin{align*} X^{\mu}(\tau,\sigma) =& x^{\mu}+p^{\mu}\tau + i\sum_{n\neq0}\frac{1}{n}\alpha_n^{\mu}\cos n\sigma e^{-in\tau} \\ X^i(\tau,\sigma) =& d_1^i +(d_2^i-d_1^i)\frac{\sigma}{\pi}+\sum_{n\neq0}\frac{1}{n}\alpha_n^i\sin n\sigma e^{-in\tau} \end{align*}

今，円状の$X^9$方向に沿ったT双対変換を考えよう．この変換$X^9_R \to -X^9_R$は，Dirichlet境界条件とNeumann境界条件を入れ替える．前述の解析を逆方向に実行すると，双対な定式化では，双対な円を巻くDブレーンのペアが存在し，$U(2)$ゲージ対称性が2つのWilsonラインによって$U(1)\times U(1)$に破れることが分かる．ボソン弦理論と同様に，元の半径$R$の円上に局在していたD$p$ブレーンは，双対な円（半径$\tilde{R}$）を巻くようになる．

したがって，一般的な規則として，T双対変換の下では巻かれているブレーンと巻かれていないブレーンが入れ替わる．元の理論のある方向にT双対変換を施し，その方向に$p$ブレーンが巻かれている場合，T双対性はこの$p$ブレーンを双対円上に局在した$(p-1)$ブレーンへと変換する．これは，IIA型超弦理論の半BPS D$p$ブレーン（$p$が偶数）が，IIB型超弦理論の半BPS D$p$ブレーン（$p$が奇数）へと写されるという要請と一致している．これらの半BPS Dブレーンのいずれかから出発すれば，T双対変換を繰り返すことで他のすべてのDブレーンに到達できる．

結合定数の像

IIA型およびIIB型超弦理論のT双対性は，弦の摂動展開の各次数ごとに成り立つ摂動論的な双対性である．IIA型超弦理論を半径$R$の円で，IIB型超弦理論を半径$\tilde{R}$の円でコンパクト化した場合，両理論はT双対変換による同一視$\tilde{R} = \alpha'/R$によって関係づけられる．これは，無次元パラメータ$\alpha'/R$の反転に相当する．次に，T双対性によって弦の結合定数がどのように写されるかを調べよう．そのためには，IIA型超弦理論のNS-NS部分の低エネルギー有効作用における結合定数依存性を考えれば十分である．具体的には， $$ \frac{1}{g_s^2}\int d^{10}x \mathcal{L}_{\text{NS}} $$ という形になる．IIB型超弦理論のNS-NS部分も同様で，IIA型の弦の結合定数$g_s$をIIB型の弦の結合定数$\tilde{g}_s$に置き換えればよい．ラグランジアン$\mathcal{L}_{\text{NS}}$の明示的な式は後の稿で与えられている．両理論を円でコンパクト化し，円方向のゼロモードのみを残すと，IIA型の場合 $$ \frac{2\pi R}{g_s^2}\int d^{9}x \mathcal{L}_{\text{NS}} $$ およびIIB型の場合 $$ \frac{2\pi\tilde{R}}{\tilde{g}_s^2}\int d^{9}x \mathcal{L}_{\text{NS}} $$ となる．T双対性は，これら2つの式が一致することを要求する．T双対の関係$\tilde{R} = \alpha'/R$を用いると，弦の結合定数の関係式 $$ \tilde{g}_s = \frac{\sqrt{\alpha'}}{R}g_s $$ が得られる．この関係は低エネルギー展開の特定の項から導かれたが，完全に一般的である．両者の弦の結合定数は比例関係にあるため，IIA型超弦理論の$g_s$による摂動展開はIIB型超弦理論の$\tilde{g}_s$による摂動展開に対応する．

K理論

Dブレーンは保存されるR-R電荷を持ち，これらはR-Rゲージ場（微分形式）のソースとなるため，電荷はゲージ場のコホモロジー類と同一視できると思われるかもしれない．これは大まかには正しいが，厳密には正しくない．適切な数学的一般化は$K$理論を用い，Dブレーンの電荷は$K$理論の類によって分類される．

II型Dブレーン

一致したII型Dブレーンの集まり（$N$個のD$p$ブレーンと$N'$個の$\overline{D$p$}$ブレーン）を考えよう．$\overline{D$p$}$は反ブレーン（antibrane）を表し，D$p$ブレーンの荷電共役である．重要な世界体積場は，次のような超接続にまとめることができる： $$ \mathcal{A}=\begin{pmatrix} A & T \\ \bar{T} & A' \end{pmatrix} $$ ここで$A$は$U(N)$ベクトル束$E$上の接続，$A'$は$U(N')$ベクトル束$E'$上の接続，$T$は$E*\otimes E'$の切断であり，$N\times N'$のタキオン場行列を記述する．ブレーンの$(p+1)$次元世界体積$X$は$E$と$E'$の底空間である．3種類の場は，それぞれ3種類の開いた弦（ブレーン同士，反ブレーン同士，ブレーンと反ブレーン，を結ぶ弦）のモードとして現れる．

ゲージ場束$E$と$E'$が位相的に同値（$E \sim E'$）であれば，完全な消滅が可能であるはずである．このためには$N = N'$となり，合計電荷がゼロである必要がある．さらに，タキオン場行列$T$は，タキオンポテンシャルの真の最小値$T = T_0$を取るべきである．もし完全な消滅が起こるなら，タキオンポテンシャルエネルギーの最小値$V(T)$は負となり，ブレーンのエネルギー密度を正確に打ち消して全エネルギーがゼロになる： $$ V(T_0)+2NT_{Dp}=0 $$

具体例として，IIB型超弦理論における$p = 9$の場合を考えよう．量子論の整合性（tadpole cancellation）のためには，全体のR-R 9ブレーン電荷が消滅する必要があり，したがって$N = N'$でなければならない．つまり，10次元時空$X$を満たすD9ブレーンと$\overline{D9}$ブレーンの数は等しくなければならない．これに関連して，2つのベクトル束$(E, E')$が現れる．ここで$E$と$E'$は階数$N$の複素ベクトル束である．

ここで，対$(E, E')$と$(F, F')$の同値性を定義したい．これは，対応する9ブレーン系がブレーン・反ブレーンの消滅や生成によって関係づけられる場合である．特に，$E \sim E'$ は純粋な真空に対応するので， $$ (E, E') \sim 0 \iff E \sim E' $$ である．さらに，同じベクトル束$H$を持つD9ブレーンと$\overline{D9}$ブレーンを追加しても，消滅が許されているため新しいものは生じない．つまり， $$ (E \oplus H, E' \oplus H) \sim (E, E') $$ このようにして，束の対の同値類を形成する．これらの類はアーベル群をなす．例えば，$(E', E)$は$(E, E')$を含む類の逆元となる．$N$と$N'$が制限されていなければ，この群は$K(X)$と表される．しかし，上記で構成した群は$N = N'$を要求する$K(X)$の部分群である．この部分群は$\tilde{K}(X)$と表される．したがって，IIB型Dブレーン電荷は$\tilde{K}(X)$の元によって分類される．これが正しく機能するかどうか調べてみよう．

この定式化は非常に一般的であるが，ここでは比較的単純な場合，すなわち$\mathbb{R}^{9,1}$内の超平面としてのD$p$ブレーンのみを考える．この目的のために，空間を接線方向と法線方向に分解するのが自然である： $$ \mathbb{R}^{9,1} = \mathbb{R}^{p,1} \times \mathbb{R}^{9-p} $$ そして，接線方向$\mathbb{R}^{p,1}$の座標に依存しない束を考える．もし場が無限遠で十分急速に減衰し，エネルギーが正則化できるなら，無限遠の点を加えて法線空間をコンパクト化し，トポロジー的に球面$S^{9-p}$となる．したがって，D$p$ブレーンの束に対する底空間は$X = S^{9-p}$となる．ここで数学的な結果を用いることができる： $$ \tilde{K}(S^{9-p}) = \begin{cases} &0 & &(p=\text{even}) \\ &\mathbb{Z} & &(p=\text{odd}) \end{cases} $$ これは，IIB型超弦理論の$\mathbb{R}^{9,1}$上に存在する全ての安定なBPS D$p$ブレーンのR-R電荷を正確に説明する．先に議論した不安定な非BPS IIB型Dブレーンは保存される電荷を持たず，この分類には現れない．

いま，いくつかの次元が次元$q$のコンパクト多様体$Q$を形成していると仮定し，全時空は$\mathbb{R}^{9-q,1} \times Q$となる．このとき，D$p$ブレーンの構成には，法線空間$\mathbb{R}^{9-p-q} \times Q$をコンパクト化して$S^{9-p-q} \times Q$を得る必要がある．これは，無限遠に$Q$のコピーを付け加えることに相当する．この場合，Dブレーン電荷を分類するための適切な数学的対象は，相対K理論群$K(S^{9-p-q} \times Q, Q)$である．特に$Q = S^1$の場合，$K(S^{8-p} \times S^1, S^1)$となる．数学的には，この相対K理論群は次の2つの部分に分解できることが知られている： $$ K(X\times S^1, S^1) = K^{-1}(X) \oplus \tilde{K}(X) $$ この式の物理的な解釈は非常に美しい．$\tilde{K}(S^{8-p})$は円に巻かれたIIB型Dブレーンを分類し， $$ K^{-1}(S^{8-p}) \cong \tilde{K}(S^{9-p}) $$ は巻かれていないDブレーンを分類する．したがって，9次元では$p < 8$のすべての値に対して加法的なDブレーン電荷が存在する．

IIA型の場合はやや微妙であり，時空を満たすD9braneはこの場合不安定である．適切なK理論群は$K^{-1}(X)$であり，これは前段落で現れたものと同じ群である．数学的な結果 $$ K^{-1}(S^{9-p}) = \begin{cases} &0 & &(p=\text{odd}) \\ &\mathbb{Z} & &(p=\text{even}) \end{cases} $$ は，$\mathbb{R}^{9,1}$内に埋め込まれた全ての安定なIIA型D$p$braneを説明する．IIA型理論を円でコンパクト化すると，相対K理論群 $$ K^{-1}(X\times S^1, S^1) = \tilde{K}(X) \oplus K^{-1}(X) $$ が得られる．この場合，$K^{-1}(X)$は円に巻かれたD-braneを，$\tilde{K}(X)$は巻かれていないDブレーンを記述する．この結果は，T双対性によって要求される通り，IIB型の場合と正確に一致する（巻かれたDブレーン$\leftrightarrow$巻かれていないDブレーン）．

I型超弦理論

orientifold射影

I型超弦理論は，IIB型超弦理論の射影から生じるものとして理解できる．IIB型超弦は向きづけられており，そのワールドシートは向きづけ可能である．ワールドシートの向き反転変換 $$ \Omega:\sigma\to-\sigma $$ はワールドシートの向きを反転させる．ワールドシート・パリティは場$X^{\mu}$および$\psi^{\mu}$の左向き・右向きのモードを入れ替える．この$\mathbb{Z}_2$変換はIIB型理論の対称性でありIIA型理論の対称性ではない．というのも，IIB型の場合にのみ左向きと右向きのフェルミオンが同じ時空におけるカイラリティを持つからである．この$\mathbb{Z}_2$対称性をゲージ化するとI型理論が得られる．射影演算子 $$ P=\frac{1}{2}(1+\Omega) $$ は物理状態の左右対称成分を保持する．したがって，得られるI型の閉弦は非向きづけであることを意味する．

I型の閉弦スペクトルは，ワールドシートの向き反転変換に対して偶である状態を残し，奇である状態を除去することで得られる．NS-NS セクターにおける質量ゼロのIIB型閉弦状態は二つのベクトルのテンソル積で与えられるが，二つのベクトルに関して対称な状態のみがオリエントフォールド射影で生き残る．これらはディラトンと重力子であり，反対称二形式$B_2$は除去される．

タイプIIB超弦理論の2つのグラビティーノ場$\Psi_1^{\mu}$と$\Psi_2^{\mu}$は，フォック空間状態 $$ b^{\mu}_{-1/2}|0;a\rangle \quad \text{および} \quad \tilde{b}^{\mu}_{-1/2}|a;0\rangle $$ に対応する．ここで添字$a$はRamondセクター基底状態のスピノル添字を示す．ワールドシートの向き反転では$|0;a\rangle$と$|a;0\rangle$が入れ替わり，左向き・右向きの励起が交換されるため，射影後に生き残るのは$\Psi_1^{\mu}+\Psi_2^{\mu}$の和のみである．同様に2つのディラティーノのうち1つだけが生き残るので，結果として質量ゼロのフェルミオン自由度は$56+8=64$となる．唯一のグラビティーノだけが残るという事実は，タイプI理論がタイプIIB理論の半分の超対称性（保存される超電荷が32個ではなく16個）しか持たないことを意味する．この超対称性は，タイプIIBの左向き・右向き超対称性の対角和に対応する．

どの質量ゼロのR-Rセクター状態がワールドシートの向き反転射影で生き残るかは，自由度の数を数えることで決定できる．スペクトルに質量ゼロのグラビティーノ場が含まれているため，理論は超対称でなければならず，したがって質量ゼロのフェルミオン自由度とボソン自由度は等しくある必要がある．これを満たす唯一の方法は，$C_0$と$C_4$を除去し，二形式$C_2$を残すことである．要約すると，射影後の質量ゼロの閉弦ボソン場はNS-NSセクターの重力子とディラトン，およびR-Rセクターの二形式$C_2$である．これにより合計で$35 + 1 + 28 = 64$のボソン自由度となり，フェルミオン自由度の数と一致する．これらは合わせて$\mathcal{N} = 1$の超重力多重項を構成する．

さらに，ツイステッド・セクターとしてタイプIの開弦を加える必要がある．これらは端点が $\Omega$ の固定点，すなわち $\sigma=0$ および $\sigma=\pi$ に対応する弦である[6]．これはすべての $X^\mu$ に対して成り立ち，開弦は常にDブレーンに終端するため，これらの開弦の存在は時空を充填するD9-ブレーンの存在を示唆する．開弦は $\Omega$ 対称性も満たさなければならないので，向き付けられていない弦である．

type IIB の基本弦（F-弦）は $B_2$ に結合する保存される電荷を持つ安定な BPS 対象である．オリエントフォールド射影によって $B_2$ が除去されるため，type I の基本弦は安定な BPS 対象ではなく，切断（分裂）し得る．ただし，切断の振幅は弦結合定数に比例するため，摂動論で想定される弱結合では type I 超弦は長寿命である．強結合では基本的な type I 弦は急速に崩壊するため，有用な概念ではなくなる．

アノマリー

第5章で述べたように，10次元Minkowski時空におけるタイプI超重力単体は重力アノマリーのために整合的ではない．さらに，アノマリーを除去する唯一の方法は，SO(32) または $E_8\times E_8$ のゲージ群を持つ超Yang-Mills理論と結合することである．タイプI超弦で可能なのは群SO(32)のみであり，これはこのゲージ群に対応するChern-Paton電荷を持つ開弦を導入することで実現される．ワールドシートのパリティ変換の下で開弦の座標は符号のいずれかで変換され得る．ラベル $i, j$ で表されるChern-Paton自由度を考慮すると，開弦状態の変換則は次のようになる： \begin{equation}\label{6.80} \Omega b^{\mu}_{-1/2}|0;ij\rangle=\pm b^{\mu}_{-1/2}|0;ji\rangle \end{equation} これはワールドシートのパリティ変換が弦の両端を入れ替えるためである．式\eqref{6.80}でプラス符号を選ぶと射影は対称行列を残し，これはシンプレクティックなゲージ群に対応する．一方，マイナス符号を選ぶと射影は反対称行列を残し，これは直交群に対応する．したがって，アノマリーのない超対称SO(32)理論を記述するためには後者の選択（マイナス符号）が必要である．

前の結論を別の見方で解釈すると次のようになる．オリエントフォールド射影により時空を充填するオリエントフォールド面が出現する．式\eqref{6.80}のプラス符号は $+16$ の D9-ブレーン電荷を持つ $O9^+$ 面を，マイナス符号は $-16$ の D9-ブレーン電荷を持つ $O9^-$ 面を出現させる．整合性のためにはこの D9-ブレーン電荷を打ち消す必要がある．これは R-R タッドポールの打ち消しに対応し，同時に全てのゲージ異常の消去も保証する．第1のケース（プラス符号）では 16 個の反D9-ブレーンを加えることで打ち消しが達成され，結果として $USp(32)$ のゲージ対称性を持つ理論となる．ただし反D9-ブレーンの存在は全ての超対称性を破る．第2のケース（マイナス符号）では 16 個の D9-ブレーンを加えることで整合性が得られ，$SO(32)$ のゲージ対称性が生じる．上述の通り，これは type IIB の二つの超対称性のうち一方を保存する．

O9面の両種類の張力は $-16T_{D9}$ である．したがって，いずれの場合も真空の全エネルギー密度はゼロとなる．超対称な $SO(32)$ の場合は，弦結合定数の任意の次数にわたって超対称性によりこれが保証される．非超対称な $USp(32)$ の場合は，自由理論に対する摂動補正によって非ゼロの真空エネルギーが生成されると予想される．

その他のI型Dブレーン

I型スペクトルで質量ゼロのR-R場は二形式C2のみである．したがってD9ブレーンを除き，オリエントフォールド射影を通過して生き残る安定なIIB型のDブレーンはこの場に結合するものだけである．これらはD1ブレーンとその磁気双対であるD5ブレーンである．

これらのDブレーンのワールドボリューム上の理論は type IIB 場合よりも複雑である．主な理由は，D1ブレーンやD5ブレーンと16枚のD9ブレーンをつなぐ開弦から生じる追加の質量ゼロモードが存在するためである．さらに，これは $O9^-$ 面の存在下で起こっている．

まず $N$ 個の重なった D1-ブレーンの系を考えよう．type IIB 理論ではそのワールドボリューム上の理論は最大超対称性を持つ $U(N)$ ゲージ理論となる．しかし type I 理論におけるオリエントフォールド面の存在のためにゲージ対称性は $SO(2N)$ へと拡張され，未破壊の超対称性は type IIB 場合の半分となる．さらに，ワールドボリューム理論には D1-ブレーンと D9-ブレーンを結ぶ開弦のモードとして生じる質量ゼロの物質超多重項が含まれ，これらは $SO(2N) \times SO(32)$ の下で $(\bm{2N}, \bm{32})$ として変換する．10 次元バルクの $SO(32)$ ゲージ対称性は D1-ブレーンのワールドボリューム理論にとって大域対称性である．

$N$ 枚の重なった D5 ブレーン系のワールドボリューム理論の解析も同様に行われる．type IIB 場合に存在する $U(N)$ ゲージ対称性は $O9$ 面の影響で $USp(2N)$ に拡張され，未破壊の超対称性は半分に減る．さらに，D5 ブレーンと D9 ブレーンを結ぶ開弦のモードとして生じる無質量の超多重項が存在し，それらは $USp(2N) \times SO(32)$ の下で $(\bm{2N}, \bm{32})$ として変換する．

タイプI Dブレーンの取りうる電荷に関するK理論による解析（ここでは示さない）は，上で列挙したすべてのDブレーンを説明する．さらに，$\mathbb{R}^{9,1}$ 内に $\mathbb{Z}_2$ 電荷を持ち超対称性を持たない安定な点状粒子の存在も予言する．したがってこの粒子は安定な非BPS D0ブレーンである．この粒子はすべてのDブレーンと同様に理論の非摂動的励起であり，またゲージ群のスピノル表示に属する．その存在は，非摂動的にはゲージ群が $SO(32)$ ではなく $\mathrm{Spin}(32)/\mathbb{Z}_2$ であることを意味する．この粒子が安定であるのは，それがスピノル表示に属する最も軽い状態であるためである．モッド2の保存則も群論から明らかであり，二つのスピノルが結合してテンソル表現を与えることができるためである．第8章ではタイプI超弦理論がヘテロティック弦理論の一つと双対であると議論されているが，タイプI理論の非BPS D0ブレーンは双対なヘテロティック理論における摂動的励起に対応する．

I'型超弦理論

次に，時空が $\mathbb{R}^{8,1}\times S^1$ の形を取り，その円の半径が $R$ である場合の I 型理論の T-双対記述を調べよう．IIB 型理論は T-双対によって IIA 型理論に写り，また I 型理論は IIB 型のオリエントフォールド射影として得られるため，結果として得られる理論は，双対円 $\tilde{S}^1$（半径 $\tilde{R}=\alpha'/R$）上にコンパクト化された IIA 型理論に対するある種のオリエントフォールド射影であることに驚くべき事はない．得られる T-双対版は I' 型理論（IA 型とも呼ばれる）と呼ばれる．

タイプII理論を円でコンパクト化した場合のT-双対性は，ワールドシート上で次の変換に対応することを思い出そう： $$ X_R \to -X_R,\quad \psi_R \to -\psi_R $$ （ここでは円に沿った成分について述べている）．これにより $$ X = X_L + X_R \to \tilde{X} = X_L - X_R $$ が導かれる．タイプII理論の場合，$\tilde{X}$ は双対円 $\tilde{S}^1$ を表す．一方，タイプI理論ではワールドシートの向き反転演算子 $\Omega$（これは $X_L \leftrightarrow X_R$ に対応する）がゲージ化されている．T-双対記述ではこれが $$ \tilde{X} \to -\tilde{X} $$ に対応することは明らかである．したがって，$\Omega$ のゲージ化は双対円に対する $\mathbb{Z}_2$ による射影（すなわち $\tilde{S}^1 = S^1/\mathbb{Z}_2$）をもたらす．より正確には，その $\mathbb{Z}_2$-作用は $\tilde{X}\to -\tilde{X}$ とワールドシート向き反転を組み合わせたオリエントフォールド射影である．前節で述べたように，$\Omega$ は IIA 理論単独では対称性にならない（左移動・右移動フェルミオンのカイラリティが逆であるため）．しかし同時に空間反転 $\tilde{X}\to -\tilde{X}$ を行えばこの不一致は補償される．

商集合 $\tilde{S}^1/\mathbb{Z}_2$ は円の半分を表す．言い換えれば，これは区間 $0 \leq \tilde{X} \leq \pi\tilde{R}$ である．円の残りの半分は鏡像として存在し，反映されている．まとめると，T-双対性の主張は，コンパクト化された IIB オリエントフォールド $$ (\mathbb{R}^{8,1}\times S^1)/\Omega $$ がタイプ IIA オリエントフォールド $$ (\mathbb{R}^{8,1}\times S^1)/\Omega\cdot\mathcal{I} $$ と等価であるということである．ここで記号 $\mathcal{I}$ は座標 $\tilde{X}\mapsto -\tilde{X}$ による反転を表す．

Type I' 構成における固定点集合は，双対座標 $\tilde{X}=0$ および $\tilde{X}=\pi\tilde{R}$ に位置する一対のオリエントフォールド8面から成る．これらはそれぞれ R-R 電荷を $-8$ 単位分持つ．Type I' 理論の整合性のためには16枚の D8-ブレーンを追加する必要があり，これらは区間 $0\leq\tilde{X}\leq\pi\tilde{R}$ の点に局在しつつ，9つの非コンパクト時空次元を満たす．これらの D8-ブレーンは明らかに，Type I 記述の D9-ブレーンの T-双対である．

D8ブレーンの区間上での位置は，type I 記述において $SO(32)$ のカルタン部分代数のウィルソン線によって決定される．$SO(32)$ はランク16であるため，カルタン部分代数は16個の生成子を持つ．対応するウィルソン線はコンパクトな $U(1)$ に属する値を取り，これらは$2\pi$で同値な角度 $\theta_I$ によって特徴づけられる．これらの角度により双対側での D8 ブレーンの位置は $$ \tilde{X}_I=\theta_I\tilde{R},\quad I=1,\ldots,16 $$ と定まる．ウィルソン線によって $SO(32)$ のゲージ対称性は破られる．type I' 記述における未破壊のゲージ対称性は次の規則で与えられる：

• 区間の内部で $N$ 個の D8 ブレーンが一致すると，未破壊の $U(N)$ ゲージ群に対応する．
• $N$ 個の D8 ブレーンが $O8^-$ 面と一致すると，未破壊の $SO(2N)$ ゲージ群が生じる．

自明なウィルソン線（すべての $\theta_I = 0$） の場合は，16枚の D8 ブレーン（およびその鏡像）がいずれかの $O8^-$ 面に重なっていることに対応する．これにより当然 $SO(32)$ のゲージ対称性が得られる．さらに 2 つの $U(1)$ 因子が存在し，対応するゲージ場は 10 次元の計量および二形式場 $C_2$ の成分（$g_{\mu 9}$ と $C_{\mu 9}$）として現れる．

より一般的には，次のようなウィルソン線を考える： $$ \theta_I=0\quad\text{for}\quad I=1,\ldots,8+N,\quad\text{and}\quad \theta_I=\pi\quad\text{for}\quad I=9+N,\ldots,16 $$ これは，$8+N$枚のD8ブレーンが$O8^-$面と一致して双対座標$\tilde{X}=0$に位置し，残りの$8-N$枚がもう一方の$O8^-$面と一致して$\tilde{X}=\pi\tilde{R}$に位置することに対応する．一般に，上で示した規則に従うとゲージ対称性は $$ SO(16+2N)\times SO(16-2N)\times U(1)^2 $$ となる．しかし，双対円の特定の半径の値においてはゲージ対称性が次のように拡張されることがある[7]： $$ SO(16-2N)\times U(1) \to E_{9-N} $$ これは非摂動的な対称性拡張であり，これまで用いてきた摂動的手法だけでは説明できない．最もよく理解されるのは第8章で扱うS双対なヘテロティック弦の記述によるものである．

背景場の存在下におけるT双対性

前節では，円でコンパクト化された弦理論のT-双対について，残りの時空次元がミンコフスキー時空であり他の背景場が消えているという仮定の下で議論した．本節では，円に沿ったT-双対変換を曲がった時空や非自明な背景場が存在する場合へと一般化する．まずNS-NS背景場（重力子 $g_{\mu\nu}$，二形式テンソル $B_{\mu\nu}$，およびダイラトン $\phi$）を検討し，続いて非自明なR-R背景場について扱う．

NS-NSセクターの場

閉じたボソニック弦のスペクトルや任意のタイプII超弦のNS-NSセクターに現れる質量ゼロの場は，時空計量 $g_{\mu\nu}$，2形式 $B_{\mu\nu}$，およびディラトン $\Phi$ からなる．これまで我々は $B_{\mu\nu}$ が零の平坦な背景のみを考えてきた．$\exp(\phi)$ の値は弦結合定数 $g_s$ を与え，これを定数でかつ小さいと仮定してきた．背景場をワールドシート作用に導入することで，より一般的な状況を解析できる．しかし作用が必要とする共形対称性は理論の整合的な解である背景に対してのみ保たれるため，任意に導入できるわけではない．うまくいく一つの単純な可能性は，全ての背景場が定数であることである．より一般的な可能性については本節で検討する．

共形ゲージにおけるワールドシート作用をNS-NS背景場を含むように一般化したものは次のように書ける： \begin{equation}\label{6.90} S=S_g+S_B+S_\Phi \end{equation} ただし \begin{align*} S_g =& -\frac{1}{4\pi\alpha'}\int d^2\sigma \sqrt{-h}h^{\alpha\beta}g_{\mu\nu}\partial_{\alpha}X^{\mu}\partial_{\beta}X^{\nu} \\ S_B =& \frac{1}{4\pi\alpha'}\int d^2\sigma \varepsilon^{\alpha\beta}B_{\mu\nu}\partial_{\alpha}X^{\mu}\partial_{\beta}X^{\nu} \\ S_{\Phi} =& \frac{1}{4\pi}\int d^2\sigma \sqrt{-h}\Phi R^{(2)} \end{align*} 第1項は明らかにミンコフスキー計量をより一般的な時空計量に置き換えたものである．第2項は基本弦がNS-NS二形式の電荷を持つことを表しており，half-BPSのDブレーンがR-R電荷を持つのと対応する．プルバックした場を微分形式で表すと，この項は引き戻した二形式$B_2$の積分に比例する．係数はその二形式の電荷が弦の張力に等しいことを示している．適切な正規化を選べば，これは超対称性によって要求される．$S_\Phi$項は$\alpha'$展開では高次の寄与である点にも注意されたい．さらに，場が定数の場合には$B$項と$\Phi$項はいずれも全微分となるが，それでも物理には重要な影響を与える．$S_B$項はワールドシートの正準運動量に寄与し，したがって正準交換関係に影響する．また，ディラトン項$S_\Phi$によって弦結合定数が正確に決定されることは第3章で説明した通りである．

背景場が円座標（例えば超弦の場合の $X^9$）に依存しない場合，$X^9$ 座標の双対化によってワールドシート理論の双対版を導出できる．これらの式は節6.1で導入したラグランジュ未定乗数法を用いて導出できる．ラグランジュ乗数 $\tilde{X}^9$ を導入し，作用を次のように考える： \begin{align*} 4\pi\alpha'S =& \int d^2\sigma [\sqrt{-h}h^{\alpha\beta}(-g_{99}V_{\alpha}V_{\beta})-2g_{9\mu}V_{\alpha}\partial_{\beta}X^{\mu}-g_{\mu\nu}\partial_{\alpha}X^{\mu}\partial_{\beta}X^{\nu} \\ &+ \varepsilon^{\alpha\beta}(B_{9\mu}V_{\alpha}\partial_{\beta}X^{\mu}+B_{\mu\nu}\partial_{\alpha}X^{\mu}\partial_{\beta}X^{\nu})+\tilde{X}^9\varepsilon^{\alpha\beta}\partial_{\alpha}V_{\beta}+\alpha'\sqrt{-h}R^{(2)}\Phi(X)] \end{align*} 上の作用において $\mu = 0, \ldots, 8$ は $X^9$ を除く全ての時空座標を指す．$\tilde{X}^9$ の運動方程式 $$ \varepsilon^{\alpha\beta}\partial_{\alpha}V_{\beta}=0 $$ は $V_{\alpha}=\partial_{\alpha}X^9$ と書くことで解かれる．これを作用に代入すると元の作用（式\eqref{6.90}）が得られる．一方で，$V_{\alpha}$ の運動方程式を用いてこの場を消去すると，双対作用 $$ \tilde{S}=S_{\tilde{g}}+S_{\tilde{B}}+S_{\tilde{\Phi}} $$ が得られる．ここで双対理論の背景場は次のように与えられる： \begin{align*} \tilde{g}_{99} =& \frac{1}{g_{99}},\quad \tilde{g}_{9\mu}=\frac{B_{9\mu}}{g_{99}},\quad \tilde{g}_{\mu\nu}=g_{\mu\nu}+\frac{B_{9\mu}B_{9\nu}-g_{9\mu}g_{9\nu}}{g_{99}}, \\ \tilde{B}_{9\mu} =& -\tilde{B}_{\mu9}=\frac{g_{9\mu}}{g_{99}},\quad \tilde{B}_{\mu\nu}=B_{\mu\nu}+\frac{g_{9\mu}B_{9\nu}-B_{9\mu}g_{9\nu}}{g_{99}} \end{align*}

ディラトンの変換則は別の解析を必要とする．第6.2節で示したように，type IIA と type IIB の結合定数は互いに関係している．$g_{99} = R^2/\alpha'$ および $\tilde{g}_{99} = \tilde{R}^2/\alpha'$ の同定を用いると，少なくとも $g_{9\mu} = \tilde{g}_{9\mu} = 0$ を仮定する場合に次が成り立つことが導かれる： $$ \tilde{\Phi}=\Phi-\frac{1}{2}\log g_{99} $$ 式(6.66)はこの関係の真空期待値として理解できる．

R-Rセクターの場

各超弦理論の質量ゼロスペクトルには，R-Rセクターに属するボソニック場も含まれている．これらをRNS形式で弦の世界面に結合して記述することには障害があり，これはRNS定式化の根本的な制約である．GS（Green–Schwarz）形式では世界面に結合させることが可能で，その場合の結合は形式的に $\bar{\Theta}\Gamma^{\mu_1\cdots\mu_n}\Theta F_{\mu_1\cdots\mu_n}$ のような形を取る．

R-R 背景場の T-双対での振る舞いを理解する一つの方法は，超弦の GS（Green–Schwarz）定式化においてこれらの場がフェルミオン場の二次形式（ビリニア）として構成される点に立ち返り，T-双対の下で右向きフェルミオンがディラック行列で乗じられるという事実（演習6.6参照）を利用することである．あるいは，それらが D-ブレーンに結合することから，D-ブレーンの T-双対性を用いて変換則を導くこともできる．どちらの方法も同じ結論に至る．結果として，type IIA 理論の R-R テンソル場に対する T-双対の作用は次のように type IIB の R-R 場を与える： $$ \tilde{C}_9=C,\quad \tilde{C}_{\mu}=C_{\mu9},\quad \tilde{C}_{\mu\nu9}=C_{\mu\nu},\quad \tilde{C}_{\mu\nu\lambda}=C_{\mu\nu\lambda9} $$ その結果，type IIA の奇数形式ポテンシャルは type IIB の偶数形式ポテンシャルに写される．これらの式は逆向き（type IIB から type IIA）にも読み替えられる．なお，これらの式は NS-NS 背景が自明な場合（$B_{\mu\nu}=0$，$g_{\mu\nu}=\eta_{\mu\nu}$，およびディラトン $\Phi$ が定数）にのみ有効であり，そうでない場合は一般化が必要である．

Dブレーンの世界体積作用

ここでDブレーンのワールドボリューム作用の構成に移ろう． 基本的な考え方は，あるDブレーン上で始まり終わる開弦のモードは，そのDブレーンのワールドボリュームに制限された場として記述できるということである．弦スケールに比べて低いエネルギー領域でDブレーンの力学を記述するには，質量ゼロの開弦モードのみを考慮すれば十分であり，それらに基づいて低エネルギー有効場理論を構成することができる．したがって，Dpブレーンに対応して，質量ゼロ場（スカラー，スピノル，ベクトル）からなる($p+1$)次元の低エネルギー有効場理論が存在し，それが当該Dブレーンの低エネルギー力学を記述する．

半分BPSのDブレーンに注目すると，$p$ は type IIA 理論では偶数で，type IIB 理論では奇数である．先に述べたように，これらは時空の超対称性の半分を保存する安定なDブレーンである．そのようなブレーンに対応して，16個の保存される超電荷を持つワールドボリューム理論が存在する．この理論を構成する方法は，GS形式と$\kappa$対称性を用いることである．この構成はここでは平坦な時空背景について行う．実際，type IIA 理論の D0-brane の場合は第5章ですでに扱われている．

いくつかの興味深い一般化が存在する．一つは曲がった背景への拡張およびNS-NSおよびR-Rセクター両方の背景場への結合である．これらの作用は後で述べるが，ボソニック部へ切り詰めた場合，すなわちκ対称性を持たない場合についてのみ記述する．特に興味深い拡張は複数の重なったDブレーンへの一般化である．この場合，ワールドボリューム理論は非可換なゲージ対称性を持ち，新たに興味深い現象が現れる．