M理論と弦の双対性

参考文献：K. Becker, M. Becker, J. Schwarz, "String Theory and M-Theory", Cambridge University Press, 2007.

1990年代半ばに起こった「第二次超弦革命」において，5つの異なる10次元超弦理論が複雑な双対性の網によって相互に関連していることが明らかになった．以前に述べたT-双対性に加え，強結合領域の弦理論を弱結合領域の対応する双対記述へと関連付けるS-双対性も存在する．さらに，超弦理論のうち2つ（IIA型超弦理論と$E_8\times E_8$ヘテロティック弦）は強結合で11次元が現れ，共通の11次元理論，すなわちM理論へと近づく．脱コンパクト化極限では，この11次元理論には弦が含まれず，弦理論ではない．

低エネルギー有効理論

この節では，M理論のいくつかの側面，特にその低エネルギー極限である11次元超重力や，様々な非摂動的な弦の双対性について説明する．これらの双対性の一部は，低エネルギー有効作用を用いて示すことができる．低エネルギー有効作用とは，弦理論のスペクトルに含まれる質量のない場の相互作用を記述する超重力理論である．非摂動的な弦理論の特徴を解析するのに，このようなアプローチが有用かどうかは自明ではない．なぜなら，弱結合から強結合への外挿は通常制御できないからである．しかし，超対称性によって保護された量に限定すれば，この方法によって驚くほど多くのことが分かる．

BPS brane

提案された双対性関係を検証する第二の方法は，これらの理論が持つ様々な超対称的，またはBogomolny-Prasad-Sommerfield（BPS）$p$-ブレーンを利用し，対応する状態のスペクトルの一致を調べることである．以下で説明するように，BPS束縛の飽和は超対称性多重項の短縮をもたらし，弱結合から強結合への信頼できる外挿が可能となる．これにより，双対理論間で$p$-ブレーンやそのテンションの詳細な一致を検証できるようになる．

BPS束縛とその飽和の概念は，4次元の質量を持つ粒子によって説明できる．$\mathcal{N}$拡張超対称性代数を，$D=4$における静止質量$M>0$の粒子空間に制限すると，次の形になる： $$ \{Q_{\alpha}^I,Q_{\beta}^{\dagger J}\}=2M\delta^{IJ}\delta_{\alpha\beta}+2iZ^{IJ}\Gamma_{\alpha\beta}^{0} $$ ここで$Z^{IJ}$はセントラルチャージ行列である．$I, J = 1,\ldots, \mathcal{N}$は超対称性のラベル，$\alpha, \beta = 1, 2, 3, 4$は各Majoranaスピノル超電荷の4成分を表す．セントラルチャージは，代数の他の生成子すべてと可換な保存量である．これらは拡張超対称性（最小の$\mathcal{N}=1$より多い超対称性を持つ理論）でのみ現れる．なぜならセントラルチャージ行列は反対称$Z^{IJ} = -Z^{JI}$だからである．セントラルチャージは，超重力多重項に属するゲージ場に結合する電荷や磁荷である．

$Z$行列はユニタリ行列$U$による変換$Z \to U^T Z U$によって，反対称行列$Z^{IJ}$を次の標準形に持ち込むことができる： $$ Z^{IJ}=\begin{pmatrix} 0 & Z_1 & 0 & 0 & \cdots \\ -Z_1 & 0 & 0 & 0 & \cdots \\ 0 & 0 & 0 & Z_2 & \cdots \\ 0 & 0 & -Z_2 & 0 & \cdots \\ \vdots & \vdots & \vdots & \vdots & \ddots \end{pmatrix} $$ ここで$|Z_1| \geq |Z_2| \geq \cdots \geq 0$である．上式の構造から，次の$2\mathcal{N} \times 2\mathcal{N}$行列 $$ \begin{pmatrix} M & Z \\ Z^{\dagger} & M \end{pmatrix} $$ は半正定値でなければならない．これは，固有値$M \pm |Z_i|$が非負であることを意味する．したがって，質量はセントラルチャージによって下から制限され，BPS束縛 $$ M \geq |Z_1| $$ が得られる．

$M = |Z_1|$を満たす状態はBPS束縛を飽和すると呼ばれる．これらは短い超多重項（BPS表現）に属する．$M > |Z_1|$の場合は長い超多重項に属する．$M = |Z_1|$のとき超対称性代数に現れるゼロが，多重項の短縮の原因となる．BPS状態の記述をさらに精密化すると，質量と等しいセントラルチャージの数を考慮する．例えば，$\mathcal{N}=4$の場合，$M = |Z_1| = |Z_2|$を満たす状態は「半BPS」，$M = |Z_1| > |Z_2|$の場合は「1/4 BPS」と呼ばれる．これらの分数は，粒子が存在するときに破れずに残る超対称性の数を表す．

以上の議論は4次元の点粒子に特有のものだが，これはD次元の$p$-ブレーンにも一般化できる．重要なのは，電荷を持つ$p$-ブレーンは$(p+1)$-形式の保存カレントを持ち，したがって$p$-形式の電荷を持つという点である．このような場合を解析するには，超対称性代数を$D$次元および$p$-形式セントラルチャージに適した形に一般化する必要がある．ここで「セントラル」と呼ぶのはやや誤解を招く表現であり，$p>0$の場合，それらはLorentz指標を持つため，Lorentz変換とは可換ではない．

上記のBPS束縛から得られる非常に重要な結論は，$M = |Z_1|$を満たすBPS状態（短い多重項に属する）は安定であるということである．質量はセントラルチャージに結びついており，超対称性が破れない限り，この関係はパラメータを変化させても変わらない．この結論が破れる唯一の方法は，他の表現がBPS多重項と縮退し，長い表現を構成できる場合である．この考え方は実は超対称性よりも一般的であり，ヒッグス機構でも同様のことが起こる．すなわち，質量のないベクトル（Lorentz群の短い表現）がスカラーと結合し，Higgsポテンシャルのパラメータが変化することで質量を持つベクトル（長い表現）になる．超対称性の場合に異なるのは，短い多重項が質量を持つことができる点である．いずれにせよ，こうした多重項の結合が起こらない限り，BPS状態を弱結合から強結合まで厳密に追跡することが可能である．これは，強結合領域における弦理論の振る舞いについての予想を検証する上で非常に重要である．

目次

• 低エネルギー有効理論
  • くりこみ可能性
  • 11次元超重力
  • IIA型超重力
  • IIB型超重力
  • I型超重力

低エネルギー有効理論

前回，各種超弦理論の状態スペクトルが弱結合極限でどのように振る舞うかを説明した．質量のない状態以外のすべての状態の質量は，$\alpha_0 \to 0$（すなわち弦のテンションが大きい）で非常に大きくなる．等価的に，他にスケールのないMinkowski空間背景では，これは低エネルギー極限に対応する．なぜなら，唯一の無次元パラメータが$\alpha_0 E^2$だからである．低エネルギー極限では，弦理論を質量のないモードのみの相互作用を記述する超重力理論で置き換えるのが良い近似となる．なぜなら，質量のあるモードは観測するには重すぎるからである．本節では，弦理論の低エネルギー極限で現れる超重力理論について説明する．これらの理論は基本的なものではないが，より根本的な弦理論の重要な特徴の一部を捉えている．

くりこみ可能性

通常のべき乗数え上げによれば，超重力理論の有効理論はくりこみ不可能である．この評価の良い指針は，作用中の各項の次元を調べることである．例えば，$D$次元のEinstein-Hilbert作用は次の形をとる： $$ S=\frac{1}{16\pi G_D}\int \sqrt{-g}Rd^D x $$ 曲率$R$は（長さ）$^{-2}$の次元を持つので，$D$次元のNewton定数$G_D$は（長さ）$^{D-2}$の次元を持つ．これは重力結合定数の2乗に比例し，したがって$D>2$の場合，負の質量次元を持つ．通常，何らかの奇跡が起こらない限り，これはくりこみ不可能性の指標となる[1]．実際，$D=4$の純粋重力の場合，そのような奇跡は起こらないことが明示的な計算で示されている．他の$D>3$の場合にも奇跡的な打ち消しが起こる理由は特にないが，それが起こらないことを証明できれば理想的である．

非くりこみ可能性は，より根本的な理論（弦理論やM理論）の低エネルギー物理を記述する有効作用としてのみ使われる理論にとっては問題にならない．有効作用に現れる無限個の高次量子補正項は，低エネルギーではほとんどの場合無視できる．しかし，これらの量子補正の一部は重要である．実際，いくつかはアノマリー解析ですでに現れていた．

M理論は，11次元超重力に対して無限個の高次元補正項を必要とすることが確かである．こうした展開は，単純な時空トポロジー（例えば$\mathbb{R}^{10,1}$）を仮定すれば，M理論によって（場の再定義を除いて）一意に決定される．次回で，$\mathbb{R}^{10,1}$において特に$R^4$項が現れることが示されている．本節では，M理論とIIA型およびIIB型超弦理論を関連付ける双対性について説明する．これらの双対性は，M理論が要求する$D=11$超重力への$R^4$補正項の正確な形を決定するために用いられてきた．

11次元超重力

M理論の低エネルギー有効作用である11次元超重力は，ここでの出発点となる理論である．この理論は1978年に構築され，その後広く研究されたが，超弦理論の地図上でその位置づけが明らかになったのは1990年代半ばであった．

1980年頃，11次元超重力に懐疑的な理由が2つあった．1つ目は，明らかな非くりこみ可能性であり，これは良く定義された量子理論の近似にはならないと考えられていた．2つ目はカイラリティ（左・右非対称性）の欠如であり，現実的なモデルに必要なカイラルな真空を持てないと考えられていた．当時探究されていた従来のKaluza-Klein枠組みでは，これらの懸念は正当だった．しかし現在では，11次元超重力はM理論の低エネルギー有効記述とみなされている．そのため，良く定義された量子論的解釈が存在する十分な理由がある．カイラリティについても状況は変わった．新たな要素として，M2ブレーンやM5ブレーン，さらには端点となる9ブレーンがある．これらは以前にも言及され，本節でもさらに議論されているが，$E_8\times E_8$ヘテロティック弦理論の強結合記述に現れ，アノマリーキャンセル要件と整合する左・右非対称性を導入する．また，M理論とカイラルな超弦理論を関連付ける非摂動的な双対性も存在する．本質的に，適切な特異点を持つ多様体へのコンパクト化によって，純粋なKaluza-Klein超重力の文脈では定義できないような場合でも，4次元でカイラリティが生じることが理解されている．

10次元超弦理論の質量のないスペクトルと比べると，11次元超重力の場の内容は比較的単純である．まず，重力を含むため，重力子が存在する．これは$SO(D-2)$（質量のない粒子のリトル群）の対称かつトレースレスなテンソルである．その物理的自由度（偏極状態）は $$ \frac{1}{2}(D-1)(D-2)-1=\frac{1}{2}D(D-3)=44 $$ となる．最初の項は対称な$(D-2)\times(D-2)$行列の独立成分数を数え，トレースレス条件により1を引いている．この理論はフェルミオンも含むため，vielbein形式を用い，重力子をvielbein場$E_A^M$で表す必要がある．11次元の場合，viel（ドイツ語で「多い」）に対し，elf（ドイツ語で「11」）bein場とも呼ばれる．$M, N, \ldots$は11次元の基空間（曲がった空間）のベクトル指標，$A, B, \ldots$は接空間（平坦空間）のベクトル指標である．前者は一般座標変換の下で，後者は局所Lorentz変換の下で非自明に変換される[2]．

局所超対称性のゲージ場はグラビティーノ場$\Psi_M$であり，これは明示的なベクトル添字$M$に加えて暗黙のスピノル添字を持つ．$M$の各値について，32成分のMajoranaスピノルとなる．スピノルを含めると，リトル群は$SO(9)$の被覆群である$Spin(9)$となる．$Spin(9)$には次元16の実スピノル表現がある．群論的には，$Spin(9)$のベクトルとスピノルのKronecker積は$9 \times 16 = 128 + 16$となる．4次元での類似の構成はスピン$3/2$とスピン$1/2$を与える．RaritaとSchwingerは，4次元の自由ベクトル-スピノル場の場合，$\Psi_M = \partial_M \epsilon$という形の局所ゲージ不変性が存在し，物理的自由度が純粋なスピン$3/2$となることを示した．任意次元での自由グラビティーノ場$\Psi_M$の運動項は次の構造を持つ： $$ S_{\Psi} \sim \int \bar{\Psi}_M\Gamma^{MNP}\partial_N\Psi_P d^{D}x $$ $\Gamma^{MNP}$の反対称性により，$\Psi_M = \partial_M \epsilon$の場合，この作用は全微分を除いて不変となる．

11次元の場合，この局所対称性により，物理的自由度は128のみとなる．したがって，これが11次元におけるグラビティーノの物理的偏極状態の数である．相互作用を含む理論では，この局所対称性は局所超対称性として同定される．この超対称性の大きさは32個の保存された超電荷を与え，これらは32成分のMajoranaスピノルを形成する．これは11次元における最小スピノルの次元であり，Lorentz不変な真空ではこれより少ない超対称性はあり得ない．また，もし超対称性がこれより多ければ，代数の表現論によりスピン2より大きい質量のない状態の存在が要求される．Minkowski時空でそのような高スピンの相互作用理論を一貫して構築することは不可能と考えられている．このため，$D > 11$で非自明な超対称理論が存在することは期待されていない．

$D=11$超重力理論が超対称的であるためには，物理的なボソン自由度とフェルミオン自由度の数が等しくなければならない．超対称性に必要な不足分のボソン自由度は，3階反対称テンソル$A_{MNP}$（3-形式$A_3$）から得られる．通常，このような形式場に対して，理論は次のゲージ変換に対して不変でなければならない： $$ A_3 \to A_3 + d\Lambda_2 $$ ここで$\Lambda_2$は二形式である．反対称テンソルゲージ場（Maxwell場も含む）では，ゲージ不変性によって独立な物理的偏極の添字は全て横方向となる．11次元の三形式の場合，物理的自由度は$9 \times 8 \times 7 / 3! = 84$となる．重力子と合わせると$44+84=128$のボソン自由度となり，理論中唯一のフェルミオン場であるグラビティーノの伝播するフェルミオン自由度128と一致する．

$A_3$のゲージ変換に対する不変性の要件は，一般座標変換や局所Lorentz変換の不変性とともに，作用の形に強い制約を与える．すべての超重力理論と同様に，次元解析によって，作用の各項において微分の数とフェルミ場の数の半分の和が2になることが決まる．この要件により，任意性はわずかな数値係数にまで減少する．最後に，局所超対称性の要件によって，$D=11$で一意な超重力理論が導かれる（規約の違いを除く）．実際，この理論は非常に強く制約されているため，その存在自体がほとんど奇跡的に思えるほどである．

11次元超重力作用のボソン部分は次の通り： $$ 2\kappa_{11}^2S=\int d^{11}x\sqrt{-G}\left( R-\frac{1}{2}|F_4|^2 \right)-\frac{1}{6}\int A_3\wedge F_4\wedge F_4 $$ ここで$R$はスカラー曲率，$F_4 = dA_3$はポテンシャル$A_3$に対応する場の強度，$\kappa_{11}$は11次元の重力結合定数を表す．11次元のNewton定数$G_{11}$，重力定数$\kappa_{11}$，11次元Planck長$\ell_p$の関係は[3] $$ 16\pi G_{11}=2\kappa_{11}^2=\frac{1}{2\pi}(2\pi\ell_p)^9 $$ 上式の最後の項はChern-Simons型であり，elfbein（または計量）に依存しない．最初の項はelfbeinに依存するが，次の計量の組み合わせのみで現れる： $$ G_{MN}=\eta_{AB}E_M^AE_N^B $$ $|F_4|^2$の量は一般的に次の規則で定義される： $$ |F_n|^2=\frac{1}{n!}G^{M_1N_1}G^{M_2N_2}\cdots G^{M_nN_n}F_{M_1M_2\cdots M_n}F_{N_1N_2\cdots N_n} $$

11次元超重力の完全な作用は局所超対称性変換に対して不変であり，場は次のように変換する： \begin{align} \delta E_M^A =& \bar{\varepsilon}\Gamma^A\Psi_M \\ \delta A_{MNP} =& -3\bar{\varepsilon}\Gamma_{[MN}\Psi_{P]} \\ \delta \Psi_M =& \nabla_M \varepsilon + \frac{1}{12}\left( \Gamma_M \bm{F}^{(4)}-3\bm{F}_M^{(4)} \right)\varepsilon \end{align} ここで次の定義を導入している： $$ \bm{F}^{(4)} = \frac{1}{4!}F_{MNPQ}\Gamma^{MNPQ} $$ および $$ \bm{F}_M^{(4)} = \frac{1}{2}[\Gamma_M,\bm{F}^{(4)}] = \frac{1}{3!}F_{MNPQ}\Gamma^{NPQ} $$ この記法の単純な一般化が以下でも使われる．$\delta\Psi_M$の式はフェルミ場の主要な次数の項を示している．(fermi)$^2\varepsilon$の形の追加項は省略されている．Dirac行列は $$ \Gamma_M=E_M^A\Gamma_A $$ を満たす．ここで$\Gamma_A$は座標に依存しない数値的な（平坦空間の）行列であり，平坦空間のDirac代数を満たす．また，角括弧は添字の単位重みでの反対称化を表す．例えば， $$ \Gamma_{[MN}\Psi_{P]}=\frac{1}{3}(\Gamma_{MN}\Psi_P+\Gamma_{NP}\Psi_M+\Gamma_{PM}\Psi_N) $$ もう一つ便利な記法として， $$ \Gamma^{M_1M_2\cdots M_n}=\Gamma^{[M_1}\Gamma^{M_2}\cdots \Gamma^{M_n]} $$ が使われている．

上式に現れる共変微分はスピン接続を含み，次のように定義される： $$ \nabla_M\varepsilon = \partial_M\varepsilon + \frac{1}{4}\omega_{MAB}\Gamma^{AB}\varepsilon $$ スピン接続はelfbeinを用いて次のように表される： $$ \omega_{MAB}=\frac{1}{2}(-\Omega_{MAB}+\Omega_{ABM}-\Omega_{BMA}) $$ ここで $$ \Omega_{MN}{}^{A}=2\partial_{[N}E_{M]}^A $$ これらの関係式は任意の次元で成り立つ．規約によっては，スピン接続にフェルミ場の二次項が含まれる場合もあるが，ここでは議論に関係しないため無視している．

超対称性変換式を示したにもかかわらず，作用のフェルミオン項を示していないことに疑問を持つかもしれない．結局のところ，フェルミオン項を含む完全な作用こそが超対称的である．しかし，このような作用や類似の作用の主な用途の一つは，古典的解を構成することである．この目的のためには，作用のボソン項のみが必要となる．なぜなら，古典的解ではフェルミオン場は常にゼロだからである．

また，解の真空対称性としていくつの超対称性が残るかを知ることも重要である．超対称的な解が与えられると，その超対称性を特徴付けるスピノル（Killingスピノル）が存在する．これはKillingベクトルの概念と類似しており，Killingベクトルは特定の解において場が不変となる無限小一般座標変換のパラメータとして現れる．これと同様に，Killingスピノルは特定の場の構成において場が不変となる無限小超対称変換をパラメータ化するスピノルである．ボソン場の超対称性変換には常に一つ以上のフェルミオン場が含まれるが，古典的にはフェルミオン場はゼロなので，これらの変換は必ず消える．したがって，解の超対称性を調べる際には，フェルミオン場を含まないフェルミオン場の変換のみが重要となる．今回の場合，Killingスピノル$\varepsilon$は次の方程式の解として与えられる： $$ \delta \Psi_M = \nabla_M\varepsilon + \frac{1}{12}\left( \Gamma_M\bm{F}^{(4)} - 3\bm{F}_M^{(4)} \right)\varepsilon = 0 $$ そして，式に含まれるボソン項が可能な超対称的解を決定する．

M理論（および11次元超重力）の重要な特徴の一つは，3-形式ゲージ場$A_3$の存在である．以前，説明したように，このような場はブレーンに結合し，ブレーンはゲージ場のソースとなる．この場合（$n=3$かつ$D=11$），3-形式は電気的には2-ブレーン（M2ブレーン）に，磁気的には5-ブレーン（M5ブレーン）に結合する．これらのテンションがBPS束縛を飽和する場合（実際にそうである），これらは安定な超対称的ブレーンとなり，そのテンションは正確に計算できる．BPS Mブレーンに注目することで，低エネルギー有効作用の展開を超えてM理論について様々な事実を知ることができる．実際，幾何学的記述の限界を示すM理論版のT-双対性さえ発見することになる．

M理論における唯一のスケールは11次元プランク長$\ell_p$である．そのため，Mブレーンのテンションは数値係数を除いて次元解析によって決定できる．II型超弦理論のブレーンとMブレーンを関連付ける双対性の議論によって確認される厳密な結果は次の通りである： $$ T_{M2}=2\pi(2\pi\ell_p)^{-3} \quad \text{and} \quad T_{M5}=2\pi(2\pi\ell_p)^{-6} $$ すべてのBPSブレーンの場合と同様に，Mブレーンも励起されてBPSでなくなることがあるが，その場合は不安定となり，式の最小BPSエネルギー密度に達するまで放射を続けることになる．

IIA型超重力

11次元超重力の作用は，各種10次元超重力理論の作用と関連している．これらは超弦理論の低エネルギー有効記述である．最も直接的な関係は，11次元超重力とIIA型超重力の間にある．その根本的な理由は，M理論を半径$R$の円でコンパクト化すると，10次元のIIA型超弦理論（結合定数$g_s = R/\sqrt{\alpha_0}$）に対応することである．この双対性については後で詳しく述べる[4]．ここで重要なのは，この関係からIIA型超重力が11次元超重力を次元簡約することで得られるという点である．次元簡約は，1つの次元を円として扱い，各場のFourier展開におけるゼロモードのみを残すことで実現される．これは，すべてのモードを低次元理論に残すコンパクト化とは対照的である．実際，IIA型超重力の作用は元々次元簡約によって構成された．この方法が最も簡単なので，以下でも用いる．

すでに述べたように，IIA型超重力の質量のないフェルミオンは，互いに逆のカイラリティを持つ2つのMajorana-Weylグラビティーノと，互いに逆のカイラリティを持つ2つのMajorana-Weylディラティーノから構成される．これらのフェルミオン場は，11次元のMajoranaグラビティーノを10次元に次元簡約することで得られる．32成分のMajoranaスピノル$\Psi_M$は，互いに逆のカイラリティを持つ一対の16成分Majorana-Weylスピノルとなる．最初の10成分が2つの10次元グラビティーノとなり，$\Psi_{11}$が2つの10次元ディラティーノとなる．IIA型ディラティーノはそれぞれ8個の物理的偏極状態を持つ．これはディラック方程式によって16成分のうち半分が独立した伝播モードを記述するためである．自由度の数が一致するためには，各グラビティーノが56個の物理的自由度を持つ必要がある．これらは$Spin(8)$の不可約表現の次元であり，ここでの議論は$Spin(9)$の128次元表現が部分群$Spin(8)$の不可約表現に分解されることとして群論的に理解できる．全体として，フェルミオン自由度は11次元と同様に128個となる．この自由度の保存は，円やトーラス上の次元簡約における一般的な特徴である．

ここでは，11次元超重力のボソン場（計量と3-形式）の次元簡約について考察する．ギリシャ文字 $\mu, \nu, \ldots$ は，11次元添字 $M, N$ の最初の10成分$(0, 1, \ldots, 9, 11)$を表す．ただし，添字10は飛ばしていることに注意．計量は次のように分解される： $$ G_{MN}=e^{-2\Phi/3}\begin{pmatrix} g_{\mu\nu}+e^{2\Phi}A_{\mu}A_{\nu} & e^{2\Phi}A_{\mu} \\ e^{2\Phi}A_{\nu} & e^{2\Phi} \end{pmatrix} $$ ここで，すべての場は10次元時空座標 $x^\mu$ のみの関数である．スカラー場 $\Phi$（後でディラトンとなる）の指数因子は，後の都合のために導入されている．11次元計量の分解から，10次元計量 $g_{\mu\nu}$，$U(1)$ゲージ場 $A_\mu$，スカラーディラトン場 $\Phi$ が得られる．次の形にも書き換えられる： $$ ds^2=G_{MN}dx^Mdx^N=e^{-2\Phi/3}g_{\mu\nu}dx^{\mu}dx^{\nu}+e^{4\Phi/3}(dx^{11}+A_{\mu}dx^{\mu})^2 $$ elfbein $E_M^A$ で表すと，この簡約は次のようになる： $$ E_M^A=\begin{pmatrix} e^{-\Phi/3}e_{\mu}^a & 0 \\ e^{2\Phi/3}A_a & e^{2\Phi/3} \end{pmatrix} $$ ここで $e_\mu^a$ は10次元のzehnbein（vielbein）である．対応する逆elfbeinは以下の通りで，後の議論で役立つ： $$ E_A^M=\begin{pmatrix} e^{\Phi/3}e_a^{\mu} & 0 \\ -e^{\Phi/3}A_{a} & e^{-2\Phi/3} \end{pmatrix} $$ $D=11$ の3-形式は，$D=10$ で3-形式と2-形式を生じる： $$ A_{\mu\nu\rho}^{(11)}=A_{\mu\nu\rho} \quad \text{and} \quad A_{\mu\nu11}^{(11)}=B_{\mu\nu} $$ 対応する場の強度は次のようになる： $$ F_{\mu\nu\rho\lambda}^{(11)}=F_{\mu\nu\rho\lambda} \quad \text{and} \quad F_{\mu\nu\rho11}^{(11)}=H_{\mu\nu\rho} $$

次元簡約を行うと，計量が非対角成分を持つため式がやや煩雑になることがある．このとき有用なテクニックは，まず接空間添字に変換することである．接空間計量の簡約は自明だからである．この動機から，次のように展開する： $$ F_{ABCD}^{(11)}=E_A^ME_B^NE_C^PE_D^QF_{MNPQ}^{(11)} $$ 添字$(A,B,C,D)$がすべて10次元か，1つが11次元かで場合分けがある： \begin{align} F_{abcd}^{(11)} =& e^{4\Phi/3}(F_{abcd}+4A_{[a}H_{bcd]}) = e^{4\Phi/3}\tilde{F}_{abcd} \\ F_{abc11}^{(11)} =& e^{\Phi/3}H_{abc} \end{align} したがって，次元簡約すると11次元の場の強度は，4形式と3形式の場の強度の組み合わせとなる： $$ \bm{F}^{(4)}=e^{4\Phi/3}\tilde{\bm{F}}^{(4)}+e^{\Phi/3}\bm{H}^{(3)}\Gamma_{11} $$ ここで$\Gamma_{11}$は10次元のカイラリティ演算子である．$\tilde{F}_4$と$H_3$は，$F_4$と同様の定義である．微分形式の記法を使うと，スケールされたテンソル場は次のように書ける： $$ \tilde{F}_4=dA_3+A_1\wedge H_3 $$ 4形式$\tilde{F}_4$が$U(1)$ゲージ変換$A_1 \to A_1 + d\Lambda$に対して不変であるためには，3形式ポテンシャルも$\delta A_3 = d\Lambda \wedge B$と変換する必要がある．このとき $$ \delta \tilde{F}_4 = d(d\Lambda \wedge B)+d\Lambda\wedge H_3=0 $$ さらに，4形式$\tilde{F}_4$はより明白なゲージ変換$\delta A_3 = d\Lambda_2$にも不変である．

$\exp \Phi$の真空期待値はIIA型超弦理論の結合定数$g_s$である．上式から，弦単位で距離が1の場合，同じ距離を11次元Planck単位で測ると$g_s^{-1/3}$となることが分かる．$g_s$が小さいと，この値は大きくなる．したがって，$g_s$が小さい場合，プランク長は弦長よりも短くなる．結果として[5]， $$ \ell_p = g_s^{1/3} \ell_s \quad \text{with} \quad \ell_s = \sqrt{\alpha'} $$

10次元では，Newton定数，重力結合定数，弦長および弦結合定数の関係は次の通り： $$ 16\pi G_{10}=2\kappa_{10}^2=\frac{1}{2\pi}(2\pi\ell_s)^8g_s^2 $$ 半径$R_{11}$の円で次元簡約を行うと，10次元と11次元のNewton定数の関係は $$ G_{11}=2\pi R_{11}G_{10} $$ 円の半径は $$ R_{11}=g_s^{2/3}\ell_p=g_s\ell_s $$ となる．

これらの公式は，この章の後半でIIA型D0ブレーンが円上の最初のKaluza-Klein励起と同一視される際に再度確認される．また，次のように定義する： $$ 2\kappa^2=\frac{1}{2\pi}(2\pi\ell_s)^8 $$ これは$2\kappa_{10}^2$と$g_s^2$の因子を除いて一致する．すなわち，$\kappa_{10}^2 = \kappa^2 g_s^2$である．

$D=10$のIIA型超重力理論のボソン作用（ストリングフレーム）は，$D=11$のボソン作用からコンパクト化座標で積分することで得られる．その結果，3種類の項が現れる： $$ S=S_{\text{NS}}+S_{\text{R}}+S_{\text{CS}} $$ 最初の項は $$ S_{\text{NS}}=\frac{1}{2\kappa^2}\int d^{10}x \sqrt{-g} e^{-2\Phi} \left( R+4\partial_{\mu}\Phi\partial^{\mu}\Phi -\frac{1}{2}|H_3|^2 \right) $$ 係数は$1/2\kappa^2$であり，弦結合定数$g_s$のべきは含まれていないことに注意．ストリングフレームの作用は，曲率スカラーの前に指数型ディラトン依存性が現れるのが特徴である．計量のワイル再スケーリングによって，この作用は通常の形のアインシュタインフレームに変換できる．この変換は演習問題である．

残りの2つの作用項 $S_{\text{R}}$ および $S_{\text{CS}}$ はR-R場に関係し，次のように与えられる： \begin{align} S_{\text{R}} =& -\frac{1}{4\kappa^2}\int d^{10}x \sqrt{-g} (|F_2|^2+|\tilde{F}_4|^2) \\ S_{\text{CS}} =& -\frac{1}{4\kappa^2} \int B_2 \wedge F_4 \wedge F_4 \end{align} 付け加えると，一般的な規則として，Euler数$\chi$のワールドシートはディラトン依存性$\exp(\chi\Phi)$を持ち，これは弦結合定数の正しい依存性を導く（以前議論）．古典的な作用のすべての項は，$\chi = -2$の球面ワールドシートに対応し，これは$g_s$の展開の先頭項を記述する．しかし，R-R場を含む$S_{\text{R}}$と$S_{\text{CS}}$の項には，期待される$e^{-2\Phi}$の因子が含まれていない．これはR-R場の定義方法によるものである．例えば，$C_1 = e^{-\Phi}\tilde{C}_1$，$F_2 = e^{-\Phi}\tilde{F}_2$（$\tilde{F}_2 = d\tilde{C}_1 - d\Phi \wedge \tilde{C}_1$）のように場を再定義すれば，すべての項に$e^{-2\Phi}$の因子が現れる．しかし通常このような場の再定義は行われず，文献で最も一般的な形で作用が表示される．

ここで，フェルミオン場の超対称性変換を主要次数で調べる．まず，重力子の変換式を次のように書き換える： $$ \delta \Psi_A=E_A^{\mu}\partial_{\mu}\varepsilon+\frac{1}{4}\omega_{ABC}\Gamma^{BC}\varepsilon+\frac{1}{24}\left( 3\bm{F}^{(4)}\Gamma_A-\Gamma_A\bm{F}^{(4)} \right)\varepsilon $$ ここでは11次元の接空間添字を用いている．これを10次元の量で解釈するには，スピン接続の各成分を計算する必要がある．混乱を避けるため，スピン接続を$\omega_{ABC}^{(11)}$と表す． $$ \omega_{aBC}^{(11)}\Gamma^{BC}=e^{\Phi/3}(\omega_{abc}\Gamma^{bc}-\frac{2}{3}\Gamma_{a}{}^{\mu}\partial_{\mu}\Phi)+e^{4\Phi/3}F_{ab}\Gamma^b\Gamma_{11} $$ および $$ \omega_{11BC}^{(11)}\Gamma^{BC}=-\frac{1}{2}e^{4\Phi/3}F_{bc}\Gamma^{bc}-\frac{4}{3}e^{\Phi/3}\Gamma^{\mu}\Gamma_{11}\partial_{\mu}\Phi $$ これらの式を用いると， $$ e^{-\Phi/3}\delta\Psi_{11}=-\frac{1}{4}e^{\Phi}\bm{F}^{(2)}\varepsilon-\frac{1}{3}\partial_{\mu}\Phi\Gamma^{\mu}\Gamma_{11}\varepsilon+\frac{1}{12}e^{\Phi}\tilde{\bm{F}}^{(4)}\Gamma_{11}\varepsilon+\frac{1}{6}\bm{H}^{(3)}\varepsilon $$ および \begin{align} e^{-\Phi/3}\delta\Psi_a=&e_a^{\mu}\nabla_{\mu}\varepsilon-\frac{1}{6}\Gamma_{a}{}^{\mu}\Phi_{\varepsilon}+\frac{1}{4}e^{\Phi}F_{ab}\Gamma^b\Gamma_{11}\varepsilon \\ &+\frac{1}{24}e^{\Phi}(3\tilde{\bm{F}}^{(4)}\Gamma_a-\Gamma_a\tilde{\bm{F}}^{(4)})\varepsilon-\frac{1}{24}(3\bm{H}^{(3)}\Gamma_a+\Gamma_a\bm{H}^{(3)})\Gamma_{11}\varepsilon \end{align}

超対称性変換式を所望の形に得るために，新しいスピノルを次のように定義する： \begin{align} \tilde{\lambda} =& e^{-\Phi/6}\Psi_{11} \\ \tilde{\Psi}_{\mu} =& e^{-\Phi/6}(\Psi_{\mu}+\frac{1}{2}\Gamma_{\mu}\Gamma_{11}\Psi_{11}) \end{align} また，$\tilde{\varepsilon} = e^{-\Phi/6}\varepsilon$とする．このとき，超対称性変換の最終的な式は次のようになる[6]： $$ \delta\lambda=\left( -\frac{1}{3}\Gamma^{\mu}\partial_{\mu}\Phi\Gamma_{11}+\frac{1}{6}\bm{H}^{(3)} -\frac{1}{4}e^{\Phi}\bm{F}^{(2)} + \frac{1}{12}e^{\Phi}\tilde{\bm{F}}^{(4)}\Gamma_{11} \right)\varepsilon $$ および $$ \delta\Psi_{\mu}=\left( \nabla_{\mu}-\frac{1}{4}\bm{H}_{\mu}^{(3)}\Gamma_{11}-\frac{1}{8}e^{\Phi}F_{\nu\rho}F_{\mu}{}^{\nu\rho}\Gamma_{11}+\frac{1}{8}e^{\Phi}\bm{F}^{(4)}\Gamma_{\mu} \right)\varepsilon $$ $\delta\Psi_{\mu}$の第2項はトーション（ねじれ）として解釈できる[7]．$\Gamma_{11}$因子のため，このトーションは反対のカイラリティ$1/2(1\pm\Gamma_{11})\varepsilon$に対して符号が逆になる． スピノル$\lambda$，$\Psi_{\mu}$，$\varepsilon$はいずれもMajoranaスピノルであり，Majorana-Weylスピノルの対に分解することもできるが，特に利点はない．したがって，これらは2つのディラティーノ，2つのグラビティーノ，および10次元の$\mathcal{N}=2$超対称性を記述する．

IIB型超重力

IIA型超重力とは異なり，IIB型理論は11次元超重力の次元簡約から得ることができない．この理論の構築の指針となるのは，超対称性とゲージ不変性である．IIB型理論の難しい特徴の一つは，自己双対な5形式場の強度が，作用を明示的に共変な形で定式化する際に障害となることである．この問題への一つの対処法は，場の方程式に注目することであり，これらは共変的に書くことができる．あるいは，自己双対性条件を補う必要がある作用を書く方法もある．

以前，IIB型超弦理論の質量のないスペクトルを導出し，これがIIB型超重力の粒子内容を与えることを示した．フェルミオン部分のスペクトルは，2つの左巻きMajorana-Weylグラビティーノ（または同等に1つのWeylグラビティーノ）と，2つの右巻きMajorana-Weylディラティーノ（または同等に1つのWeylディラティーノ）から構成される．NS-NSボソンは，計量（またはzehnbein），2-形式$B_2$（場の強度$H_3 = dB_2$），およびディラトン$\Phi$からなる．R-Rセクターは，形式場$C_0$，$C_2$，$C_4$から構成される．このうち$C_4$は自己双対な場の強度$\tilde{F}_5$を持つ．

自己双対な5形式場の存在は，IIB型超重力の古典的な作用を記述する際に大きな困難をもたらす．この問題は，2次元や6次元の類似の自己双対テンソルでも生じる．例えば， $$ \int |F_5|^2 d^{10}x $$ のような作用では，自己双対性の制約が組み込まれておらず，伝播する自由度が本来の2倍になってしまう．自己双対性条件を課すためにラグランジュ乗数場を導入しても，その場自体が除去すべき成分を再び導入してしまうため，問題は解決しない．

自己双対場の問題への対処法はいくつか存在する．元々のアプローチは作用を構成せず，場の方程式と超対称性変換のみを記述することである．これはほとんどの目的に十分であり，超重力理論はあくまで有効理論であり，経路積分に挿入するような量子理論ではないからである．基本的な考え方は，方程式の超対称変換が別の方程式（または方程式の組み合わせ）を与えるべきだということである．この手法を体系的に追求すると，超対称性変換と場の方程式を同時に決定することが可能となる．実際，方程式は非常に強く制約されているため，多くの整合性チェックが得られる．

PST（Pasti, Sorokin, Tonin）の方法に従い，補助スカラー場と補償的なゲージ対称性を適切に導入することで，正しい自由度を持つ明示的に共変な作用を定式化することが可能である．追加されたゲージ対称性を利用すれば，補助スカラー場をゲージ固定として時空座標の一つに等しく設定できるが，その場合，ゲージ固定後の理論はその方向に関して明示的な一般座標不変性を持たなくなる．それでも，この理論は少なくともこのゲージ選択がグローバルに定義できるような時空トポロジーに対しては正しいものである．

ここではPSTアプローチには従わず，自己双対性条件を追加の制約として課すことで正しい運動方程式を与える作用を提示する．このような作用は超対称的ではない．なぜなら（制約なしでは）ボソン自由度がフェルミオン自由度より多くなるためである．さらに，上述の理由により，この制約を作用に組み込むことはできない．

この作用を発見する方法は，まず超対称的な運動方程式を構成し，次に自己双対性条件を手動で課したときにそれらの方程式を再現する作用を書き下すことである．こうして得られるIIB型超重力のボソン部分の作用は次の形になる： $$ S=S_{\text{NS}}+S_{\text{R}}+S_{\text{CS}} $$ ここで$S_{\text{NS}}$はIIA型超重力理論と同じ表現であり，質量のないR-Rセクターの場を記述する作用部分は次の通り： \begin{align} S_{\text{R}} =& -\frac{1}{4\kappa^2}\int d^{10}x\sqrt{-g}\left( |F_1|^2+|\tilde{F}_3|^2+\frac{1}{2}|\tilde{F}_5|^2 \right) \\ S_{\text{CS}} =& -\frac{1}{4\kappa^2} \int C_4 \wedge H_3 \wedge F_3 \end{align} これらの式において，$F_{n+1} = dC_n$，$H_3 = dB_2$であり， \begin{align} \tilde{F}_3 =& F_3-C_0H_3 \\ \tilde{F}_5 =& F_5-\frac{1}{2}C_2\wedge H_3+\frac{1}{2}B_2\wedge F_3 \end{align} これらはIIA理論の$\tilde{F}_4$に類似したゲージ不変な組み合わせである．ここに現れるR-R場は，Dブレーンのワールドボリュームに単純に結合する場とは場の再定義によって異なっている．自己双対性条件を満たす5-形式は$\tilde{F}_5$，すなわち $$ \tilde{F}_5=\star\tilde{F}_5 $$ である．この条件は，作用から導かれる運動方程式を補う制約として課す必要がある．

ここで提示した作用は超対称的な理論のボソン部分ではないが，制約を含む場の方程式自体は超対称的である．すなわち，前述の通り，これらの方程式の超対称性変換は，変換後に方程式自体を課すことで消える．IIB型超重力の超対称性変換式は後の章で必要となるため，ここで示しておく．

ディラティーノとグラビティーノ場をそれぞれWeylスピノル$\lambda$と$\Psi_\mu$で表す．同様に，無限小超対称性パラメータはWeylスピノル$\varepsilon$で表される．IIB型超重力のフェルミオン場の超対称性変換（フェルミオン場の主要次数）は次の通り： $$ \delta\lambda=\frac{1}{2}(\partial_{\mu}\Phi-ie^{\Phi}\partial_{\mu}C_0)\Gamma^{\mu}\varepsilon+\frac{1}{4}\left( ie^{\Phi}\tilde{\bm{F}}^{(3)}-\bm{H}^{(3)} \right)\varepsilon^{\star} $$ および $$ \delta\Psi_{\mu} = \left( \nabla_{\mu}+\frac{i}{8}e^{\Phi}\bm{F}^{(1)}\Gamma_{\mu}+\frac{i}{16}e^{\Phi}\tilde{\bm{F}}^{(5)}\Gamma_{\mu} \right)\varepsilon-\frac{1}{8}\left( 2\bm{H}_{\mu}^{(3)}+ie^{\Phi}\tilde{\bm{F}}^{(3)}\Gamma_{\mu} \right)\varepsilon^{\star} $$

IIB型理論の$SL(2,\mathbb{R})$対称性は，上記の方程式では明示的ではないため，これを明示的に示す方法を簡単に説明する．理論には2つの2形式ポテンシャル，$B_2$と$C_2$があり，これらは$SL(2,\mathbb{R})$対称群の下でダブレットとして変換する．したがって，対称性が明示的になるように作用を書き直すため，2形式ポテンシャルを$B_2 = B_2^{(1)}$，$C_2 = B_2^{(2)}$と名付け，2成分ベクトル表記を導入する： $$ B_2=\begin{pmatrix} B_2^{(1)} \\ B_2^{(2)} \end{pmatrix} $$ 同様に，$H_3 = dB_2$も2成分の縦ベクトルとなる．変換 $$ \Lambda=\begin{pmatrix} d & c \\ b & a \end{pmatrix} \in SL(2,\mathbb{R}) $$ に対して，$B$場は次の規則で線形に変換する： $$ B_2 \to \Lambda B_2 $$ パラメータが定数であるため，$H_3$も同様に変換する． 複素スカラー場 $$ \tau = C_0+ie^{-\Phi} $$ は，次のよく知られた規則で非線形に変換するため便利である： $$ \tau \to \frac{a\tau + b}{c\tau + d} $$ 場$C_0$は時にアクシオンと呼ばれ，理論（超重力近似）には$C_0 \to C_0+定数$というシフト対称性がある．そのため，複素場$\tau$はアクシオン-ディラトン場と呼ばれることもある．

この作用は，対称な $SL(2,\mathbb{R})$ 行列 $$ \mathcal{M} = e^{\Phi} \begin{pmatrix} |\tau|^2 & -C_0 \\ -C_0 & 1 \end{pmatrix} $$ を用いて便利に書くことができる．この行列は次の単純な規則で変換する： $$ \mathcal{M} \to (\Lambda^{-1})^T \mathcal{M} \Lambda^{-1} $$ 標準的なアインシュタインフレーム計量 $g^E_{\mu\nu}$ と四形式 $C_4$ は $SL(2,\mathbb{R})$ 不変である．ディラトンが変換するため，タイプIIBのストリングフレーム計量 $g_{\mu\nu}$は，標準的なアインシュタイン計量と $$ g_{\mu\nu}=e^{\Phi/2}g_{\mu\nu}^{E} $$ の関係があり，$SL(2,\mathbb{R})$ 不変ではない．スカラー曲率項のこの変数変換下での変換は次の通り： $$ \frac{1}{2\kappa^2}\int d^{10}x \sqrt{-g} e^{-2\Phi} R \to \frac{1}{2\kappa^2}\int d^{10}x\sqrt{-g}(R-\frac{9}{2}\partial^{\mu}\Phi\partial_{\mu}\Phi) $$ 最初の式ではストリングフレーム計量，二番目の式ではアインシュタインフレーム計量が使われている．

上記で定義した量を用いると，タイプIIB超重力の作用は次の形に書き換えることができる： \begin{align} S =& \frac{1}{2\kappa^2}\int d^{10}x \sqrt{-g} \left( R-\frac{1}{12}H_{\mu\nu\rho}^T\mathcal{M}H^{\mu\nu\rho}+\frac{1}{4}\mathrm{tr}(\partial^{\mu}\mathcal{M}\partial_{\mu}\mathcal{M}^{-1}) \right) \\ &-\frac{1}{8\kappa^2}\left( \int d^{10}x\sqrt{-g}|\tilde{F}_5|^2+\int\varepsilon_{ij}C_4\wedge H_3^{(i)}\wedge H_3^{(j)} \right) \end{align} ここでは，計量 $g^E$ が全体で使われている．この作用はグローバルな $SL(2,\mathbb{R})$ 変換に対して明示的に不変である．

この形式で課される自己双対性方程式，すなわち $\tilde{F}_5 = \star \tilde{F}_5$ は，$SL(2,\mathbb{R})$ 不変でもある．これを確認するには，まず $\star \tilde{F}_5$ を定義するHodge双対がWeyl再スケーリングに対して不変であることに注意する．したがって，ストリングフレーム計量でもアインシュタインフレーム計量でも定義できる．式の $\tilde{F}_5$ の定義は，明示的に $SL(2,\mathbb{R})$ 不変な形に書き換えることができる： $$ \tilde{F}_5=F_5+\frac{1}{2}\varepsilon_{ij}B_2^{(i)}\wedge H_3^{(j)} $$ このとき，自己双対性方程式の不変性が従う．

I型超重力

場

前に説明したように，I型超弦理論はIIB型超弦理論のオリエンティフォールド射影として現れる．これは，IIB型閉弦スペクトルを左右対称な状態に切り詰めるとともに，開弦からなるツイストセクターを追加することを意味する．質量のない閉弦セクターは10次元の$\mathcal{N}=1$超重力であり，質量のない開弦セクターはゲージ群SO(32)を持つ10次元の$\mathcal{N}=1$超Yang-Mills理論である．したがって，低エネルギー有効作用は，$\alpha'$展開の先頭次数でこれら2つの超多重項の相互作用を記述するべきである．

理論をボソニック部門に制限すると，10次元のType I超弦理論の質量のない場は次の通りである． $$ g_{\mu\nu},\quad \Phi,\quad C_2,\quad A_{\mu} $$ ここで $g_{\mu\nu}$ は重力子，$\Phi$ はディラトン，$C_2$ はR-R二形式，$A_{\mu}$ はツイストセクターに由来するSO(32)のYang-Millsゲージ場である．

作用

ストリングフレームでは，type I superstring の低エネルギー極限を記述する超対称ラグランジアンのボソニック部は次の通りである． $$ S=\frac{1}{2\kappa^2}\int d^{10}x \sqrt{-g}\left[ e^{-2\Phi}(R+4\partial_{\mu}\Phi\partial^{\mu}\Phi)-\frac{1}{2}|\tilde{F}_3|^2-\frac{\kappa^2}{g^2}e^{-\Phi}\mathrm{tr}(|F_2|^2) \right] $$ ここで $F_2 = dA + A\wedge A$ はゲージ場 $A = A_{\mu}dx^{\mu}$ に対応する Yang-Mills の場の強度である．さらに， $$ \tilde{F}_3=dC_2+\frac{\ell_s^2}{4}\omega_3 $$ であり，これは Chapter 5.8 のアノマリー解析で説明した通りである．完全な弦理論において Chern-Simons 項は $$ \omega_3=\omega_L-\omega_{YM} $$ で与えられる．ここで $$ \omega_L=\mathrm{tr}(\omega\wedge d\omega+\frac{2}{3}\omega\wedge\omega\wedge\omega) $$ および $$ \omega_{YM}=\mathrm{tr}(A\wedge dA+\frac{2}{3}A\wedge A\wedge A) $$ である．ここで $\omega_L$ はローレンツの Chern-Simons 項（$\omega$ はスピン接続）で，$\omega_{YM}$ は Yang-Mills の Chern-Simons 項である．しかしながら，$\omega_L$ は高次の導関数項であるため，低エネルギー有効超重力理論に含まれるのは $\omega_{YM}$ のみである．

パラメータ $g$（式 (8.73) で導入）は，10次元の Yang-Mills 結合定数 $g_{YM}$ と次の関係にある． $$ \frac{g_{YM}^2}{4\pi}=\frac{g^2}{4\pi}g_s=(2\pi\ell_s)^6g_s $$ Type I 超弦理論では，$g_{YM}$ は開弦の結合であり，したがって $g_{YM}\propto\sqrt{g_s}$ となる．Chapter 3 で述べたように，これは開弦がワールドシートの境界に結合するのに対して，閉弦はワールドシートの内部点に結合するという事実に起因する． 次節で扱うヘテロティック弦理論では，このカウントがやや異なる．そこでの $g_{YM}$ は閉弦の結合であり，したがって $g_{YM}\propto g_s$ となる．

式(8.73)の最初の2項は球面ワールドシート（$\chi = -2$）に由来するのに対し，最後の項は円板ワールドシート（$\chi = -1$）に由来することに注意．三番目の項はR-R場に関係するため，前述のとおり$\chi$に依存しない．

式 (8.73) は，10次元における $N=1$ 超重力が $SO(32)$ の超Yang-Mills 理論と結合したものを記述している．したがって，type I 超弦理論の有効作用の低エネルギー展開における先頭項のみを含む．この場合，作用に対するいくつかの高次補正は既にアノマリー解析から知られている．具体的には，上で述べたように，$\tilde{F}_3$ の定義に現れる Chern-Simons 項は完全理論では Yang-Mills 成分と Lorentz 成分の両方を含むが，Lorentz の Chern-Simons 項は導関数の高次であるため，先頭の低エネルギー有効作用には含まれていない．アノマリー取消のために必要な局所的カウンタ項 $$ \int C_2\wedge Y_8 $$ もまた，前述の作用に含まれる次元より高い項のみから構成されている．

超対称変換

ここで，type I の有効作用を不変に保つ超対称変換を考える．超重力多重項に関係する項は，前に示した type IIB の超対称変換をトランケーションすることで得られる．type IIB の式は複素フェルミオン場（例えば $\psi=\psi_1 + i\psi_2$）を用いて記述されており，$\lambda$ や超対称性パラメータ $\varepsilon$ も同様である．type I へのトランケーションでは生き残る組合せは $\psi=\psi_1+\psi_2$ のような和で与えられる Majorana-Weyl 場であり，$\lambda$ や超対称性パラメータも同様である．この規則を用いると，type I の場合に超重力多重項のフェルミオンの変換は次のようになる． \begin{align*} \delta\Psi_{\mu} =& \nabla_{\mu}\varepsilon-\frac{1}{8}e^{\Phi}\tilde{\bm{F}}^{(3)}\Gamma_{\mu}\varepsilon \\ \delta\lambda =& \frac{1}{2}\backslash{\partial}\Phi\varepsilon+\frac{1}{4}e^{\Phi}\tilde{\bm{F}}\varepsilon \\ \delta\chi =& -\frac{1}{2}\bm{F}^{(2)}\varepsilon \end{align*} 最後の式は超 Yang-Mills 多重項の随伴フェルミオン $\chi$ の超対称変換を表す．常に言われているように，これらの式にはフェルミオンの二次の修正項が存在するが，Killing スピノル方程式を構成するためにはそれらは必要ない．

ヘテロティック超重力

Chapter 7では，十次元Minkowski時空におけるヘテロティック弦理論の粒子スペクトルを導出した．$SO(32)$ヘテロティック弦理論の質量のない場の内容は，type I superstring theoryのそれと完全に一致する．$E_8\times E_8$ヘテロティック弦の質量のない場はゲージ群の置き換えによってのみ異なるが，質量のある励起状態に関しては差異がより大きい．

作用

10次元のストリングフレームにおける二つのヘテロティック理論の低エネルギー有効作用のボソニック部は次のようになる． $$ S=\frac{1}{2\kappa^2}\int d^{10}x \sqrt{-g}e^{-2\Phi}\left[ R+4\partial_{\mu}\Phi\partial^{\mu}\Phi-\frac{1}{2}|\tilde{H}_3|^2-\frac{\kappa^2}{30g^2}\mathrm{Tr}(|F_2|^2) \right] $$ ここで，全作用が球面ワールドシートに由来することと，ヘテロティック理論にはR-R場が存在しないため，すべての項が$e^{-2\Phi}$の因子を含んでいる点に注意する．$F_2$はゲージ群$SO(32)$あるいは$E_8\times E_8$に対応する場の強度であり， $$ \tilde{H}_3=dB_2+\frac{\ell_s^2}{4}\omega_3 $$ は次の関係式を満たす． $$ d\tilde{H}_3=\frac{\ell_s^2}{4}\left( \mathrm{tr}R\wedge R-\frac{1}{30}\mathrm{Tr}F\wedge F \right) $$ しかしながら，type Iの文脈で指摘したように，Lorentz項は先頭の低エネルギー有効理論には含まれない．ここで$\mathrm{Tr}$と表したゲージ理論の跡は496次元の随伴表現における跡である．Chapter 5で議論したように，これは$SO(32)$の32次元基底表現における跡$\mathrm{tr}$を用いて次の恒等式で書き換えられる． $$ \mathrm{tr}F\wedge F=\frac{1}{30}\mathrm{Tr}F\wedge F $$ この表記は$E_8\times E_8$理論でも用いられることがあるが，この群は32次元表現を持たない点に注意する．この表記を用いる場合，$\mathrm{tr}R\wedge R$と$\mathrm{tr}F\wedge F$のコホモロジー類は等しくなければならない．なぜなら$d\tilde{H}_3$は正確形だからである．

超対称変換

ヘテロティック弦の有効作用は10次元で$N=1$の局所超対称性を持つため，gravitino場$\Psi_{\mu}$はMajorana–Weylスピノルである．dilatino場$\lambda$もMajorana–Weylスピノルである．フェルミオン場の変換のボソン部，すなわちKillingスピノル方程式を読み取るのに必要な部分は次の通りである． \begin{align*} \delta\Psi_{\mu} =& \nabla_{\mu}\varepsilon-\frac{1}{4}\tilde{\bm{H}}_{\mu}^{(3)}\varepsilon \\ \delta\lambda =& -\frac{1}{2}\Gamma^{\mu}\partial_{\mu}\Phi\varepsilon+\frac{1}{4}\tilde{\bm{H}}^{(3)}\varepsilon \\ \delta\chi =& -\frac{1}{2}\bm{F}^{(2)}\varepsilon \end{align*} 最初の2つの変換は，type IIBの超対称変換を$N=1$の部分理論にトランケートし，NS–NS場のみを残すことで導出できる．この定式化の利点は，$\tilde{H}_3$の$\Psi_{\mu}$への寄与がトーションとして解釈できる点である．

S-duality

S-双対性は，結合定数$g_s$を持つ弦理論を結合定数$1/g_s$を持つ（場合によっては異なる）理論と結びつける変換である．これは，T-双対性が半径$R$の円形次元を半径$\ell_s^2/R$の円に対応させるやり方に類似している．いずれの場合も，パラメータはスカラー場の真空期待値によって与えられる．したがって，双対性はより基本的なレベルでは場の変換として理解できる．

Maxwellの方程式が電気量と磁気量を入れ替える操作に対して持つ対称性は，Diracの量子化条件と組み合わせることで，場の理論におけるその種の双対性の可能性を既に示唆している．この強・弱（あるいは電気・磁気）双対性は非可換ゲージ理論へと一般化される．最も分かりやすい例は$N=4$超対称Yang–Mills（SYM）理論であり，この理論は共形不変な量子理論で，これはChapter 12で重要な役割を果たす．実際に$N=4$ SYMの定義に$\theta$項を含めると（そうすべきである），この理論は$SL(2,\mathbb{Z})$双対性を持ち，複素結合定数 $$ \tau=\frac{\theta}{2\pi}+i\frac{4\pi}{g_{YM}^2} $$ はモジュラーパラメータとして変換する．理論が共形不変であることは，$\tau$が任意のくりこみスケールに依存しない定数であることを保証する．単純な電気・磁気双対性 $g_{YM}\to 4\pi/g_{YM}$ は，$\theta=0$のときの特殊な場合として$\tau\to -1/\tau$に対応する．他の超対称ゲージ理論の電気・磁気双対性の理解には近年大きな進展があり，その出発点は1994年のSeiberg and Wittenによる$N=2$ゲージ理論に関する重要な仕事である．

二重展開

これらの様々な弦の双対性とその関係を理解するために，弦理論を二つのパラメータによる同時展開として見ることが有用である．

• 一つは Regge slope（あるいは逆弦テンション）$ \alpha' $である．$ \alpha' $ による展開は点粒子極限に対する弦らしさの展開である．数学的には，これは弦のワールドシート理論の量子力学的扱いに対応する摂動展開であり，ワールドシート作用の係数が $1/\alpha'$ であることから $ \alpha' $ はプランク定数 $ \hbar $ に類似した役割を果たす．$ \alpha' $ は（長さ）$^2$の次元を持つため，無次元の展開パラメータは $ \alpha' p^2 $（$p$ は特徴的な運動量・エネルギー）や $ \alpha'/L^2 $（$L$ はコンパクト次元の大きさなどの特徴長さ）とできる．
• 二つ目の展開は弦結合定数 $g_s$ に対するものである．$g_s$ はディラトン場 $\phi$ の指数化した期待値であり，これは弦ループの数，すなわちワールドシートの種数に対応する展開である．

S-双対とT-双対は非常に類似している．しかし，S-双対は弦ループ展開に対して非摂動的であるためより深いように見える．一方，T-双対はループ展開の各次数ごとに成り立ち，特に先頭（tree または classical）近似で有効である．

type I 超弦理論：$SO(32)$ヘテロティック弦との双対性

Type I と $SO(32)$ ヘテロティック理論の低エネルギー有効作用は非常に似ている．特に，これらは単純な変換 $$ \Phi \to -\Phi $$ と計量の Weyl 再スケーリング $$ g_{\mu\nu} \to e^{-\Phi}g_{\mu\nu} $$ の組合せによって互いに写像される．したがって，標準的なアインシュタイン計量 $g^{E}_{\mu\nu}=e^{-\Phi/2}g_{\mu\nu}$ は不変な組合せとなる．他のボソン場は変更されない（$A$ や $B_2$，$C_2$ など）．

これにより，両方の弦理論（低エネルギー極限に限らない）が同一の量子論のパラメータ空間の異なる領域における記述であるという双対性が導かれる．弦結合定数は各場合において$\exp(\Phi)$の真空期待値であるため，式(8.88)は type I 超弦の結合定数が SO(32) ヘテロティック弦の結合定数の逆数であることを示す． $$ g_s^I g_s^{H}=1 $$ したがって，一方の理論が弱結合であるとき他方の理論は強結合になる．もちろん，このために type I とヘテロティックの双対性を厳密に証明することは困難である．上述した有効作用の解析以外にもいくつかの検証が行われており，矛盾は見つかっていない．さらに重要なのは，これは複雑で過剰に制約された双対性の網の一つの接点であり，もしどれか一つでも誤っていれば全体の構成が崩れることになる．

非摂動的な検証

双対性の非摂動的検証の例として，type I 理論の D-ストリングを考える．そのテンションは $$ T_{D1}=\frac{1}{g_s}\frac{1}{2\pi\ell_s^2} $$ である．この弦が SO(32) ヘテロティック弦と同一であるという仮説を検証する．ヘテロティック弦のテンションは $$ T_{F1}=\frac{1}{2\pi\ell_s^2} $$ であり，弱結合から強結合へ外挿したものと仮定する．D-ストリングは BPS を飽和する超対称的対象であり，したがってテンションの式は $g_s$ の値に関わらず正確であるはずだ．これらの式を比較するには，物理量としてのスケールが両者で同じでも，Weyl 再スケーリングにより異なる計量で測られていることを考慮する必要がある．したがって，Weyl 再スケーリング（Eq. (8.89)）により $$ \ell_s \to \ell_s\sqrt{g_s} $$ となる．これと変換規則 $g_s\to 1/g_s$ を組み合わせると，$T_{D1}$ と $T_{F1}$ が一致することが確認できる．さらに，変換 $g_s\to 1/g_s,\ \ell_s\to \ell_s\sqrt{g_s}$ は二乗して恒等変換になるため，その逆変換と同じであることに注意．

これらの弦に双対する磁気電荷を持つ5ブレーンのテンションも同様に比較できる．これは既述の議論から保証されているが，念のため確認しておく．Type I 理論では $$ T_{D5}=\frac{1}{g_s(2\pi)^5\ell_s^6} $$ ヘテロティック理論では $$ T_{NS5}=\frac{1}{(g_s)^2(2\pi)^5\ell_s^6} $$ 再び，これらは要求される方法で互いに写像される．

基本的なtype I 弦

SO(32)ヘテロティック弦がtype IのD弦と同一視できることを見た後，SO(32)ヘテロティック理論の中に基本的なtype I弦の対応物が存在するか疑問に思うかもしれない．これに答えるためには，両者の弦の本質的な違いを理解することが重要である．type IのF弦は保存量を持たず，超対称でもない．基本的なtype IIB弦に結合する二形式$B_2$はオリエンティフォールド投影によってスペクトルから除かれている．type IのF弦が切れる理由については正しい見方が二つある．一つは時空を満たすD9-braneが存在し，基本弦はD-brane上で切れるという説明である．もう一つは保存量を持たず超対称でもないため，切断を防ぐ保存則自体が存在しないという説明である．type I弦の切断振幅は$\sqrt{g_s}$に比例するため，結合定数が十分小さいとこれらの弦は長寿命になり得る．これは摂動展開の基礎となる基本的対象として扱うには十分である．しかし，type Iの結合定数が大きい場合は図8.1に示すようにこれらのF弦は分解し，もはや有用な概念ではなくなる．したがって，弱結合のヘテロティック記述にはそれらの痕跡は現れない．

type IIB S-duality

Type IIB supergravity は以前述べたように大域的な $SL(2,\mathbb{R})$ 対称性を持つ．しかしこの低エネルギー有効作用の対称性は完全な type IIB superstring theory には共有されない．実際，様々な弦理論的および量子的効果によって無限離散部分群 $SL(2,\mathbb{Z})$ に破られる． これを示す一つの方法は，本理論における安定な弦を考えることである．NS–NS 二形式 $B_2$ と R–R 二形式 $C_2$ という二つの二形式ゲージ場が存在するため，弦が持ちうる電荷は二種類ある．F-string（fundamental string）は電荷 $(1,0)$ を持ち，これは $B_2$ に結合する電荷を1単位持ち，$C_2$ に結合する電荷は持たないことを意味する．同様に D-string は $C_2$ に結合し，電荷 $(0,1)$ を持つ． 二形式が $SL(2,\mathbb{R})$ のダブレットを成すため，これらの弦もダブレットとして変換する．一般には $(p,q)$ 弦に変換し，両方の種類の電荷を同時に持つ．これらの電荷が Dirac の量子化条件によって整数であることを保証するためには，$SL(2,\mathbb{Z})$ 部分群への制限が不可欠である．

$g_s\to1/g_sの下での対称性$

Type IIB超重力では複素場 $$ \tau=C_0+ie^{-\Phi} $$ が$SL(2,\mathbb{R})$の下で非線形に変換する．この性質は完全な弦理論でも維持されるが，群は離散部分群$SL(2,\mathbb{Z})$に制限される．特に変換$\tau\to -1/\tau$は$C_0=0$で評価するとディラトンの符号を反転させ，弦結合定数$g_s$をその逆数に写す．これはtype Iと$SO(32)$heterotic理論を結ぶようなS-双対性変換であり，この場合はtype IIB superstring theoryを自己に対応させる．さらに，これは無限の双対性群$SL(2,\mathbb{Z})$の一要素にすぎない．この双対性群は本節冒頭で議論した$N=4$ SYMのそれと著しい類似性を示す．これは偶然ではないことがChapter 12で示される．

$(p,q)$弦

$(p,q)$弦は同等に扱われ，したがってすべてが超対称的である．このことは各弦のテンションが超対称性によるBPS境界を飽和することを意味し，それがテンションを一意に決定する．ストリングフレームでは，結果は次のようになる： $$ T_{(p,q)}=|p-q\tau_B|T_{F1}=T_{F1}\sqrt{\left( p-q\frac{\theta_0}{2\pi} \right)^2+\frac{q^2}{g_s^2}} $$ ここで真空期待値を $$ \tau_B=\langle \tau \rangle=\frac{\theta_0}{2\pi}+\frac{i}{g_s} $$ と定義し， $$ T_{F1}=T_{(1,0)}=\frac{1}{2\pi\ell_s^2} $$ とする．この結果は，$(p,q)$弦を type IIB 超重力の場方程式のソリトン解として構成することで導ける．これらの方程式が超弦の方程式に対する近似にすぎないという事実はテンションの値を得る上で問題にならない．なぜならテンションは超対称性の帰結だからである．後で，type IIB 理論と M-theory を結ぶ双対性からこのテンション式を導いて確認する．

F-弦のテンションの式はすべての値の$\theta_0$で有効であるが，通常のD-弦のテンション式 $$ T_{D1}=T_{(0,1)}=\frac{T_{F1}}{g_s} $$ は$\theta_0=0$のときにのみ成り立つ．また，$\theta_0=2\pi$のときの$(p,q)$弦は$\theta_0=0$のときの$(p-q,q)$弦と同等である．

これらの $(p,q)$ 弦のテンションは次の三角不等式を満たす $$ T_{(p_1+p_2,q_1+q_2)}\leq T_{(p_1,q_1)}+T_{(p_2,q_2)} $$ 等号が成り立つためには，ベクトル $(p_1,q_1)$ と $(p_2,q_2)$ が平行である必要がある．結論の一つの表現は，$(p,q)$ 弦は $p$ 本の F-弦と $q$ 本の D-弦の束縛状態とみなせるということである．同じ電荷を持つ他のどの構成よりもテンションが低いのは，$p$ と $q$ が互いに素のときに限る．もし公約数が存在するなら，同じ電荷と同じテンションを持つ複数本弦の構成が存在する．

その他のBPS状態

ここで他のBPS type IIBブレーンの$SL(2,\mathbb{R})$に関する性質を簡単に考察する．

• D3ブレーンは$C_4$に結合する電荷を持つため，$SL(2,\mathbb{R})$のシングレットとして振る舞う．このため任意の$(p,q)$弦がD3ブレーンに終着できるという興味深い帰結がある．なぜならF-弦を$(p,q)$弦に変える$SL(2,\mathbb{R})$変換はD3ブレーンを不変に保つからである．
• 安定な超対称的$(p,q)$5-ブレーンが存在し，これらは$(p,q)$弦の磁気双対である．それらの$SL(2,\mathbb{R})$に関する性質は$(p,q)$弦と類似している．
• D7ブレーンは$C_0$に磁気的に結合する．$C_0$は$SL(2,\mathbb{R})$の下でかなり複雑に変換するため，7-ブレーンの分類は直ちには明らかでない．この問題は本節では追求しないが，F-theoryで記述されるtype IIB超弦理論の非摂動的真空には様々な7-ブレーンが含まれるため，分類は重要である．これは後で扱う．

F-stringが終端できるp-ブレーンとしてのD-braneの定義は，$p=1$の場合には注意して解釈する必要がある．素朴に「fundamental stringがD-stringに終端する」と解釈すると，3本の弦セグメントの接続を想起させる．そのうち1本が$(1,0)$で，残り2本が$(0,1)$であるような構成だ．しかしこれは正しくない．fundamental stringの端にある電荷はフラックスを生み，そのフラックスは付接するいずれかの弦セグメントに流れ込まなければならないため，その過程で弦の電荷が変化してしまうからだ．要するに，3本の弦の接続は電荷保存を満たさねばならない．つまり，電荷が$(p^{(i)},q^{(i)})$で$i=1,2,3$の3本の弦の許される接続は，次式を満たす必要がある． $$ \sum_i p^{(i)}=\sum_i q^{(i)}=0 $$ 数学的には，これはフェインマン図の頂点における運動量保存（2次元の場合）と同じである．接続の構成は，弦の張力をベクトルとして扱ったときにその和が零になるよう角度が選ばれていれば安定である．このような接続を用いて複雑な弦のウェブを構築することができる．

M理論

M理論という用語はWittenによって導入され，先頭の低エネルギー有効作用が$11$次元超重力となる$11$次元の「謎めいた」あるいは「魔術的」な量子理論を指すために用いられた．M理論はまだ完全には定式化されていないが，その存在を示す証拠は非常に説得力がある．例えば，それはtype IIB超弦理論と同程度に根源的である（ただしそれ以上ではない）．実際，後者は弦理論であるため明確な摂動展開を持ち，その分ややよく理解されている．この節では，M理論をトーラス上でコンパクト化したものとtype IIB超弦理論を円上でコンパクト化したものとを結びつける双対性を説明する．この双対性は特定の幾何学的な設定を要求するため，一方の理論の解（あるいは量子真空）を他方の理論の記述へ書き換えられるのは適切な幾何学のクラスに限られる．

M理論を有効作用の観点で記述することは明らかに根本的ではないため，弦理論家は代替的な定式化を模索している．正確な非摂動的定式化の一案としてMatrix theoryと呼ばれる提案があり，これはChapter 12で議論される．しかしこれは背景幾何の限られたクラスにしか適用できないため，話の全てではない．より一般的なアプローチであるAdS/CFT dualityもChapter 12で扱われる．

強結合におけるIIA型超弦理論

IIA型超弦理論の低エネルギー極限はIIA型超重力であり，この超重力は既に述べたように$11$次元超重力の次元簡約によって得られる．しかし，IIA型超弦理論とM理論の対応はそれよりもはるかに深い．そこで，IIA型超弦理論の強結合極限を詳しく見ていく．

D0-brane

Type IIA superstring theory は安定な非摂動励起であるD0-braneを持ち，string frameにおけるその質量は$g_s^{-1}$で与えられる．この事象は，M-theoryを円でコンパクト化した視点から見ると，massless supergravity multipletの最初のKaluza–Klein励起として解釈できるという主張がある．全256次元の超多重項はしばしばsupergravitonと呼ばれる．この主張を検討するために，11次元超重力（あるいはM-theory）を円でコンパクト化した場合を考える．11次元におけるsupergravitonの質量はゼロである： $$ M_{11}^2=-p_Mp^M=0,\quad M=0,1,\ldots,9,11 $$ 10次元ではこれは次の形になる： $$ M_{10}^2=-p_{\mu}p^{\mu}=p_{11}^2,\quad \mu=0,1,\ldots,9 $$ 円方向の運動量$p_{11}$は量子化され，$p_{11}=N/R_{11}$であるため，10次元での質量スペクトルは $$ (M_N)^2=(N/R_{11})^2,\quad N\in\mathbb{Z} $$ というKaluza–Klein励起の塔を表す．これらの状態は短い（256次元の）超対称性多重項を成すため，いずれもBPS状態であり，保存される$U(1)$量子数$N$を持つ．$N=1$の場合，D0-braneとの対応のためには $$ R_{11}=\ell_s g_s $$ である必要があり，これはSection 8.1で示した結果と一致する．D0-braneは$g_s\to 0$のときに張力が発散するためIIA理論の非摂動的励起である．したがって，この対応はIIA理論と11次元M-theoryの双対性を，摂動論を越えて検証する手段を与える．

$R_{11}=g_s\ell_s$ により，コンパクト化の半径は弦結合定数に比例する．これは摂動領域 $g_s\to 0$ が $R_{11}\to 0$ の極限に対応することを意味する．逆に強結合極限，すなわち $g_s\to\infty$ は円形の第11次元の非縮退化をもたらし，10次元の空間を特別視しない11次元の理論へと至る．このように得られる11次元の理論が M-theory であり，その低エネルギー極限は11次元超重力である．

議論を逆にたどると，これはD0-braneの結合状態の存在に関する非自明な結果を支持する強力な証拠である．$N$番目のKaluza–Klein励起は，$N$単位の電荷を持つ10次元の安定な粒子の多重項を与える．したがって，これらは$N$個のD0-braneの束縛状態と見なせる．ただし，これらは非常に特別なタイプの束縛状態であり，結合エネルギーがゼロである．これらの状態はBPS束縛を飽和しているため結合エネルギーの余地がない．つまり，$N$単位のD0-brane電荷を持つ状態として許される限りにおいて最も軽いということである．これはまた，式(8.105)の質量公式が$g_s$のすべての値に対して正確であることを意味する．前に述べたように，BPS質量公式が破られる唯一の方法は，短い超多重項が長い超多重項に変化することである．しかしながら，そのために必要な自由度はこの場合存在しない．

結合エネルギーがゼロの束縛状態はしきい値束縛状態と呼ばれる，それらが安定かどうかは非常に微妙な問題である．Kaluza–Klein 観点からはそれらが安定であるべきことは明白だが，type IIA 理論における D0-brane の力学的観点からはまったく自明ではない．実際，証明は非-Fredholm 作用素族に対する指標定理を含む高度に技術的なものである．しかもその結果はこの特定の問題に固有である．重なった BPS 状態がしきい値束縛状態を形成しない場合が他にも存在する．すでに触れた例は type IIB の $(p,q)$ 弦に関するものであり，これらの弦は $p$ と $q$ が互いに素である場合にのみ安定な束縛状態となる．

M-brane

M理論のBPSブレーンはM2ブレーンとM5ブレーンである．M理論（11次元）には弦は含まれない．ここで次の疑問が生じる．理論がM理論に移行する強結合領域で，IIA型の基本弦はどうなるのか．もっともらしい推測は，IIA型のF-弦は第11次元の円を巻いたM2ブレーンであるということである．テンションはエネルギー密度であるため，この同一視は次を要求する： $$ T_{F1}=2\pi R_{11}T_{M2} $$ この関係はテンション $$ T_{F1}=\frac{1}{2\pi\ell_s^2},\quad T_{M2}=\frac{2\pi}{(2\pi\ell_p)^3} $$ と $R_{11}=g_s\ell_s$ および $\ell_p=g_s^{1/3}\ell_s$ を用いて確かめられる．これらの関係は前節で示した通りであり，ここでの提案はそれらが正しいことを裏付ける．他のブレーンも同様に対応づけられる．例えば，D4ブレーンは空間円を一方向に巻いたM5ブレーンと同一視される．

興味深い別の事実は，F-弦がD4ブレーンに終端するIIA型配置のM理論起源を考えることで導ける． 上の議論から，これは明らかに円形次元を巻いた各MブレーンにおいてM2ブレーンがM5ブレーンに終端する事象に対応する． IIA型のF-弦がDブレーンに終端できる理由の一つは，弦の端にある電荷に対応するフラックスがDブレーンのワールドボリュームの1形式ゲージ場によって運ばれるからである． この場合，Mブレーンでは対応する機構が何かを問うことができる． M2ブレーンの端はM5ブレーン内部の弦である．したがってM5ブレーンのワールドボリューム理論は対応するフラックスを運ぶための2形式ゲージ場 $A_2$ を含まなければならない． 実際にその通りであり，対応する場の強度 $F_3$ は自己双対である．これは type IIB 超重力における5形式場強度と同様である．

D6-brane

前節の議論は、IIA型のD$p$-brane（$p=0,2,4$）が巻きつけられたまたは非巻きつけのM-braneに由来することを説明した．これにより、M理論の観点からD6-braneをどのように理解すべきかという疑問が生じる．明らかに他のD-braneとは異なり、D6-braneは単純にM2-braneやM5-braneと対応づけられるものではない．この問題に答える鍵は、D6-braneがD0-braneの磁気双対であり、D0-braneが$x^{11}$の円に沿ったKaluza–Klein励起として解釈されることを思い出す点にある．D0-braneは$U(1)$ゲージ場$C_{\mu}=g_{\mu 11}$に対して電気的な電荷を持つ．したがって、D6-braneは同じゲージ場に磁気的に結合するはずである．

この問題は，円でコンパクト化された純粋重力の$5$次元の場合についてはるか昔に解かれている．この場合，課題は四次元で磁気電荷を持つソリトンであるKaluza–Klein単極子を記述する$5$次元計量を構成することである．この解を6つの平坦な次元とテンソル積を取れば，まったく同じ構成が$11$次元の問題に適用される．余分な6つの平坦な次元はD6-braneの世界体積の空間方向を構成する．

関連する5次元の幾何は5次元でRicci-flatかつ非特異であり，次のように与えられる． $$ ds_5^2=-dt^2+ds_{TN}^2 $$ ここでTaub-NUT metricは $$ ds_{TN}^2=V(r)(dr^2+r^2d\Omega_2^2)+\frac{1}{V(r)}(dy+R\sin^2(\theta/2)d\phi)^2 $$ ここで $d\Omega_2^2$ は単位2球面の標準計量である． $$ V(r)=1+\frac{R}{2r} $$ また，磁場は次のように与えられる． $$ \vec{B}=-\vec{\nabla}V=\vec{\nabla}\times\vec{A},\quad A_{\phi}=R\sin^2(\theta/2) $$ ここではベクトルポテンシャルの非零成分のみを表示している．Taub-NUT metricは座標 $y$ の周期が $2\pi R$ のときに $r=0$ で非特異となる．したがって実際の円の半径は $$ \tilde{R}(r)=V(r)^{-1/2}R $$ であり，$r\to\infty$ のとき $R$ に近づき，$r\to 0$ のときゼロになる．

Taub-NUT metricで記述されるソリトンの質量はエネルギー密度$T_{00}$を積分して計算できる．D6-braneのテンションを理解するために，さらに6つの平坦な次元を加えると次を得る． $$ T_{D6}=\frac{2\pi R}{16\pi G_{11}}\int d^3x\nabla^2V $$ 積分は$2R$を与えるので， $$ T_{D6}=\frac{(2\pi R)^2}{16\pi G_{11}}=\frac{2\pi R}{16\pi G_{10}}=\frac{2\pi}{(2\pi\ell_s)\7g_s} $$ ここで$R=g_s\ell_s$を用いた．これはChapter 6で得られた値と一致する．

上の単一中心解の単純な一般化として，多中心Taub-NUT計量があり，これは$N$本の平行なD6-braneの系を記述する． $$ ds^2=V(\vec{x})d\vec{x}\cdot d\vec{x}+\frac{1}{V(\vec{x})}(dy+\vec{A}\cdot d\vec{x})^2 $$ ここで $$ \vec{B}=-\vec{\nabla}V=\vec{\nabla}\times\vec{A},\quad V(\vec{x})=1+\frac{R}{2}\sum_{\alpha=1}^{N}\frac{1}{|\vec{x}-\vec{x}_{\alpha}|} $$ この系はBPSであるため，張力と磁気荷は単一のD6-braneの値の$N$倍に等しい．

同様の構成は円でコンパクト化された他の弦理論にも当てはまる．実際，円でコンパクト化された type IIB superstring theory には，D6-brane と同様の方法で構成される Kaluza-Klein 5-brane が含まれており，これは Kaluza-Klein 0-brane の磁気双対である．円方向に沿った T-双対変換は type IIB 理論を双対円上にコンパクト化された type IIA 理論へと変換する．Kaluza-Klein 0-brane は双対円に巻かれた基礎的な type IIA string と双対である．したがって Kaluza-Klein 5-brane は基礎的な IIA 弦の磁気双対である type IIA NS5-brane に写像されるはずである．

強結合における$E_8\times E_8$ヘテロティック弦理論

Hořava–Wittenによる強結合$E_8\times E_8$ヘテロティック弦理論の構図を簡潔に概説する．まず，強結合のIIA型超弦理論，あるいは同等に$M$理論を$\mathbb{R}^{9,1}\times S^1$上で考え，ある$\mathbb{Z}_2$対称性で割る．これはtype IIBからtype Iを導くときの手続きに類似している．この場合の適切な$\mathbb{Z}_2$対称性は次の反転を含む： $$ x^{11} \to -x^{11}\quad A_3 \to -A_3 $$ 特にこの$\mathbb{Z}_2$作用で割ると，$x^{11}$方向のフーリエ展開における$A_3$のゼロモードはスペクトルから除かれ，一方 $$ B_{\mu\nu}=A_{\mu\nu11} $$ のゼロモードは残る．これは十次元の$N=1$超重力が質量ゼロの二形式を含み，質量ゼロの三形式を含まないことと整合するために必要である．ヘテロティック弦の結合定数$g_s$は $$ g_s=R_{11}/\ell_s $$ で与えられ，IIAの場合と同様である．

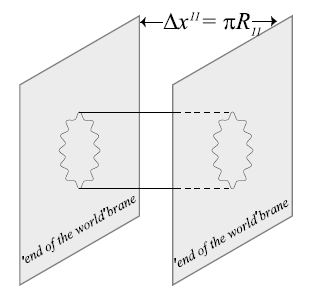
空間 $S^1/\mathbb{Z}_2$ は $x^{11}=0$ から $x^{11}=\pi R_{11}$ までの線分と見なせる．両端点はオービフォールドの固定点である．このことは興味深い物理像をもたらす．すなわち，11次元時空は厚さ $\pi R_{11}$ のスラブとして見なすことができ，両方の10次元境界はオービフォールド特異点であり，超 Yang–Mills の場が局在している．これらの境界はしばしば end-of-the-world 9-branes と呼ばれる．それぞれが E8 のゲージ場を担う．この直感的な説明は理論が同一の因子を二つ持つゲージ群を持つ理由を示す．境界が E8 のゲージ超多重項を担うことはアノマリー取消のために必須である．奇数次元では境界がなければアノマリーは生じないが，境界上に現れるアノマリーを打ち消せるのは E8 のみであり，ほかの選択肢は成り立たない（see Chapter 5）．

別の経路から，M-theory を $S^1/\mathbb{Z}_2$ にコンパクト化したものが10次元の $E_8\times E_8$ ヘテロティック弦理論に双対であることを導ける．この手法は，これまでに導入した次の双対性の連鎖を用いる： (1) $E_8\times E_8$ ヘテロティック弦と $SO(32)$ ヘテロティック弦の間の T-双対性， (2) $SO(32)$ ヘテロティック弦と type I superstring の間の S-双対性， (3) type I superstring と type I' superstring の間の T-双対性， (4) type I' superstring を type IIA の orientifold と同定すること， (5) type IIA superstring と円上の M-theory の双対性． この構成の定量的な詳細は Exercise 8.6 に記載されている．

M2-brane は円柱位相を持ち，時空の境界に終端できる．したがって M2-brane の境界は end-of-the-world 9-brane の内部にある閉曲線となる．この図では，$E_8\times E_8$ heterotic string は二つの時空境界の間に吊るされた円柱状の M2-brane と見なせ，それぞれの境界に一つの E8 が対応する．この円柱は分離距離 $R_{11}$ が小さいとき，図8.2に示すように十次元に存在する弦として良く近似される．$g_s$ に関する摂動論は $R_{11}=0$ の周りの展開であるため，実際に11次元が存在し弦が実は膜であるという事実はその方法では見えない．したがってヘテロティック弦のテンションは次のようになる． $$ T_H=2\pi R_{11}T_{M2}=(2\pi\ell_s^2)^{-1} $$ これらの記述は強結合の type IIA superstring theory に関する記述の対応物である．

$E_8\times E_8$ヘテロティック弦理論には強結合極限が二通り考えられる．一つは両側の境界が無限遠に離れる極限で，結果として11次元の時空幾何が得られる．これはIIA型超弦理論から出発して$R_{11}\to\infty$とする場合と同じ極限である．強結合の$E_8\times E_8$ヘテロティック弦とIIA型超弦理論は11次元のバルクにおいて同一であり，両者を区別するのは前者に境界が存在するかどうかだけである． 第二の可能性は，$R_{11}\to\infty$とする際に一方の境界を固定することである．この極限は半無限な第11次元をもたらす．この極限では境界が一つしかないため，E8ゲージ群も一つだけ存在する．この極限は文献でほとんど注目されていない．また，二つより多くの境界を持つ11次元幾何を考え，それに対応して二つより多くのE8群を持つ場合も考えられる．

強結合の $E_8\times E_8$ ヘテロティック弦の現象論的応用を調べる研究では，ヘテロティックM-theoryとも呼ばれるこの分野においてさらに6つの空間次元をコンパクト化（通常は Calabi–Yau 多様体上で）することを考える．弱結合の10次元記述では現れない興味深い可能性の一つは，この6次元空間のモジュライやディラトンの vev のような他のモジュライが，コンパクトな第11次元の長さに沿って変化し得ることである．したがって，例えば一方の $E_8$ 理論がもう一方よりも強結合になっていることがあり得る．この点については Chapter 10 でさらに詳述する．

M理論の双対性

前節では，強結合領域にあるIIA型超弦理論と強結合領域にある$E_8\times E_8$ヘテロティック弦が，単純なM理論による解釈を持つことを示した．M理論は他の超弦理論や自分自身と対応づける追加の双対性も持つ．

M理論/IIB型超弦理論 双対性

円でコンパクト化したM-theoryはtype IIA超弦理論を与え，またtype IIA超弦理論を円でコンパクト化すると双対円上のtype IIB超弦理論に対応する．これら二つを合わせると，M-theoryを二次元トーラス$T^2$上に置いた理論と，type IIB超弦理論を円$S^1$上に置いた理論の間に双対性が存在するはずだと結論づけられる．M理論のトーラスは面積$A_M$とモジュラス$\tau_M$で特徴づけられ，IIB側の円は半径$R_B$を持つ．ここではtype IIA理論を介さずにこの双対性を直接調べる．具体的には，9次元における様々なBPS状態やブレーンを比較する．

Type IIB superstring theory におけるすべての $(p,q)$ 弦は $SL(2,\mathbb{R})$ 変換で結びつくため，互いに同等であり，任意の一種が弱結合で扱える．しかし，あるものが弱結合であるとき，他のすべては必然的に強結合となる．任意の $(p,q)$ 弦を考え，弱結合極限におけるその9次元励起のスペクトルを Chapter 6 に示した標準的な弦理論の公式を用いて書き出す． $$ M_B^2=\left( \frac{K}{R_B} \right)^2+(2\pi R_B W T_{(p,q)})^2+4\pi T_{(p,q)}(N_L+N_R) $$ 前と同様に，$K$ は Kaluza–Klein 励起数，$W$ は弦の巻き数である．$N_L$ と $N_R$ は左移動・右移動振動モードの励起数であり，レベル整合条件は $$ N_R-N_L=KW $$

計画は，上の式をすべての$(p,q)$弦に対して同時に用いることである．しかし，強結合ではその式はまったく無意味であり，最多でも一種類の弦しか弱結合にならない．この場合の適切な手法はBPS状態のみを考えることである．すなわち短い超対称性多重項に属する状態である．これらは質量公式を強結合へ信頼して外挿できる．識別は容易で，$N_L=0$または$N_R=0$で与えられる．（$N_L=N_R=0$のものは超短縮である．）このようにして，スペクトルの非常に大きな部分に対して正確な質量公式を得ることができる．これは任意の摂動限界に現れるものよりもはるかに多い．もちろん，この豊富なBPS状態の出現はコンパクト化に強く依存する．

三つの整数 $W, p, q$（$p$ と $q$ は互いに素）と任意の整数対 $n_1, n_2$ の間には一意の対応がある．対応は $(n_1,n_2)=(Wp,Wq)$ で与えられる．整数 $W$ は $n_1$ と $n_2$ の最大公約数である．ただし $W$ を選ぶか $-W$ を選ぶかの曖昧さがあるが，$W$ は（向き付けられた）巻き数であり $(-p,-q)$ 弦は向きを反転した $(p,q)$ 弦なので，両者は実際には同値である．したがって BPS 状態は三つの整数 $K,n_1,n_2$ と，振動子励起 $N_L=|W K|$ に対応する項と $N_R=0$ 部分からの16次元の短縮多重項のテンソル積（またはその逆）によって特徴付けられる．なお，式 (8.123) に現れる組合せ $|W|T_{(p,q)}$ は式 (8.97) を用いて次の形に書き換えられる． $$ |W|T_{(p,q)}=|n_1-n_2T_B|T_{F1} $$