フラックスコンパクト化

参考文献：K. Becker, M. Becker, J. Schwarz, "String Theory and M-Theory", Cambridge University Press, 2007.

モジュライ空間問題

1つ前のノートでは，積空間 $M_4 \times M$ におけるCalabi-Yauコンパクト化について説明した．10次元ヘテロティック弦理論をこのような多様体上でコンパクト化すると，得られる低エネルギー有効作用は $\mathcal{N}=1$ 超対称性を持ち，これは現象論的に様々な点で魅力的である．特定のCalabi-Yauコンパクト化では，3世代モデルが得られる場合もある．

これらのモデルの非現実的な特徴は，質量を持たないスカラー場が真空期待値（vev）が未定のまま含まれていることである．そのため，多くの物理量（例えば結合定数など）について具体的な予測を行うことができない．これらのスカラー場は「モジュライ場」と呼ばれ，そのvevは低エネルギー4次元有効作用においてポテンシャルを持たないモジュライである．この「モジュライ空間問題」または「モジュライ安定化問題」は，従来の弦理論文献では認識はされていたが，強調されてはいなかった．しかし，弦の双対性の発見と，braneが弦理論で重要な役割を果たすことが認識されたことで，この状況は変化した．

モジュライ空間問題はすでに$D=11$超重力の単純な円コンパクト化でも現れる．この場合，円の大きさがモジュライとなり，これはtype IIAディラトンのvev（真空期待値）と双対であり，値が未定である．同様の問題は，より複雑な状況として，任意の超弦理論の通常のCalabi-Yauコンパクト化におけるコンパクト空間の体積についても現れる．この場合，内部多様体の大きさは決定できない．

ワープしたコンパクト化

最近，弦理論研究者たちは，モジュライ場を安定化するポテンシャルを生成する方法を理解した．このためには，弦理論を新しいタイプの背景幾何学，すなわちワープした幾何学上でコンパクト化する必要がある[1]．ワープしたコンパクト化は，超弦理論やM理論の宇宙論に対しても興味深いモデルを提供する．さらに，これらは弦理論とゲージ理論の双対性にも関連している．

ワープした幾何学では，特定のテンソル場の背景が消えず，対応するフラックスが内部多様体のサイクルを貫いている．$n$-形式ポテンシャル $A$ と $(n+1)$-形式の場の強さ $F = dA$ があるとき，磁気フラックスは[2] $$ \int_{\gamma_{n+1}} F $$ の形で与えられ，この値はサイクル $\gamma_{n+1}$ のホモロジーのみに依存する．同様に，$D$次元では同じ場が電気フラックス $$ \int_{\gamma_{D-n-1}} \star F $$ を与える．ここで $\star$ は$D$次元でのHodge双対を表す．このフラックスもサイクル $\gamma_{D-n-1}$ のホモロジーのみに依存する．

フラックス量子化

ここでは，フラックスコンパクト化がモジュライ空間問題に与える影響について考察し，この分野の最近の進展を紹介したい．関与するフラックスには強い制約が課されており，これはクォークやレプトンの質量などの物理パラメータについて予測を行う上で重要である．運動方程式を満たす$n$-形式テンソル場の形を導出し，それらのうちどれが超対称性を保存し，どれが保存しないかという重要な問題についても議論する．

運動方程式に加えて，もう一つの制約としてフラックス量子化条件が現れる．braneがフラックスの源となる場合，量子化は単純に理解できる．すなわち，（適切に規格化された）サイクルを囲むフラックスは，囲まれたbraneの数となり，これは整数である．非自明なホモロジーを持つ多様体では，brane源がなくても非自明なサイクルを通るフラックスが整数値に量子化される場合がある．この場合，量子化は一般化されたDirac量子化条件の結果である．特殊な場合には，曲率による効果によってフラックス量子化則に分数のオフセットが生じることがある．例えば，M理論では，$D=11$超重力作用への高次量子重力補正によってこのような効果が現れる．

フラックスコンパクト化

まず，M理論を共形的Calabi-Yau four-fold 上でコンパクト化する場合を考える．この場合，計量はCalabi-Yau計量に共形因子を掛けた形になる．これらのモデルは，3次元Minkowski時空を導くため現象論的には非現実的だが，場合によっては4次元の $\mathcal{N}=1$ 理論と関連している．この比較的単純なモデル群は，フラックスコンパクト化の主要な特徴の多くを示している．より複雑な例として，type IIBやヘテロティックのフラックスコンパクト化が次に議論される．後者の場合，非ゼロのフラックスは内部コンパクト化多様体が非Kählerだが複素多様体であることを要請する．これらは捩率を持つ接続を用いて記述するのが便利である．

ディラトンとラジアルモジュラス

モジュライの例としては，ディラトン（その値が弦の結合定数を決定する）や，ラジアルモジュラス（その値が内部多様体の大きさを決定する）が挙げられる．結合定数が十分小さい場合，弦ループやインスタントン補正を無視した古典的解析が正当化される．同様に，内部多様体の大きさが弦のスケールより十分大きい場合，超重力近似が弦理論に対して正当化される．これら2つのモジュライを固定するポテンシャルが存在しない場合（フラックスがない場合），これらのモジュライは調整可能であり，これらの近似が任意によく成立するようにできる．したがって，フラックスのないコンパクト化は現実的ではないものの，少なくとも数式の有効性の領域が存在することは確信できる．フラックスコンパクト化でディラトンやラジアルモジュラスが安定化される場合はこの点が自明ではないが，M理論を共形Calabi-Yau four-fold上でフラックスコンパクト化する場合にも超重力近似の有効性の領域が存在することが示される．

より一般的には，モジュライ場はフラックスコンパクト化によって動的に安定化される．これは望ましいことであるが，新たな課題も生じる．ラジアルモジュラスやディラトンの値が安定化された場合，古典的な超重力近似がそもそも有効であると言えるのか，どう確信できるだろうか？一般に，安定化されるモジュライの数と，数学的な制御の度合いの間にはトレードオフが存在する．現実的なモデルでは全てのモジュライが安定化されるべきなので，これは課題となる．全てのモジュライが固定され，かつ超重力近似が正当化できるモデルも知られている．これらのモデルでは，フラックスは整数値 $N$ をとり，$N$ を十分大きくすることで超重力記述が大きな $N$ の極限で有効となる．

ランドスケープ

フラックスコンパクト化によって弦理論コンパクト化で現れるモジュライ場を安定化できるものの，別の問題が存在する．フラックスコンパクト化では，フラックスが多くの異なる離散値をとれるため，可能な真空状態が非常に多数生じる．そして，それらの中から選択するための基準は知られていない．これらの真空は，弦理論のランドスケープを記述するあるポテンシャルの極値とみなすことができる．この問題への一つのアプローチとして，大きな縮退を受け入れ，統計的手法を用いて典型的な真空の一般的特徴を記述する方法について議論したい．

フラックスと双対ゲージ理論

特定の背景（通常は非ゼロのフラックスを含む）における超弦理論が，双対なゲージ理論記述を持つことが示されている．最も単純な例として，共形不変なゲージ理論を含む．しかし，超重力の双対記述を与える，閉じ込め型超対称ゲージ理論に対応するモデルも存在する．type IIB理論の文脈で閉じ込め型ゲージ理論に双対なフラックスモデル，すなわちKlebanov-Strassler（KS）モデルについて説明したい．このモデルの双対ゲージ理論的側面は別のところで議論する．

brane-worldシナリオ

通常のKaluza-Kleinコンパクト化とは異なる方法として，「brane-worldシナリオ」がある．このアプローチの目的の一つは，ゲージ階層問題，すなわち重力が他の力に比べて非常に弱い理由を説明することである．基本的な考え方は，可視宇宙が標準模型の場が閉じ込められた3-braneであり，それが高次元時空に埋め込まれているというものである．もちろん，追加次元は実験的にはまだ観測されていないが，この枠組みでは観測可能性が完全に否定されるわけではない[3]．標準模型の場は3-braneに閉じ込められている一方で，重力は全ての$4+n$次元に伝播する．$(4+n)$次元の背景幾何学が因子化可能でない，すなわちワープ因子を含む場合（弦理論のフラックスコンパクト化のように），階層問題が解決できることを示したい．実際，弦理論のフラックスコンパクト化は幾何学にワープ因子を与え，これが階層問題の解決策となり得る．これは，弱スケールで超対称性が破れるというより一般的な階層問題へのアプローチとは異なるものである．

フラックスと超弦宇宙論

標準的なビッグバン宇宙論（SBB）は，宇宙の多くの特徴，例えば宇宙マイクロ波背景放射（CMB）の存在を説明する現在受け入れられている理論である．CMBは宇宙の放射の大部分を占めており，この放射はほぼ等方的で，黒体スペクトルの形をしている．しかし，この放射には小さな不規則性があり，これはSBBで記述される時代の前に，宇宙が急速な膨張期（インフレーション）を経験したと仮定しなければ説明できない．インフレーションはSBB理論の初期条件を与える．インフレーションの様々なモデルが提案されているが，最終的にはインフレーションを弦理論のような根本的な理論から導く必要がある．これはフラックスコンパクト化の文脈で現在非常に活発に研究されている分野である．宇宙論は弦理論を検証する最も劇的な方法の一つを提供する可能性があり，宇宙規模の弦，すなわち宇宙ひもが生成される可能性もある．

目次

• フラックスコンパクト化とCalabi-Yau four-folds
  • Calabi-Yau four-fold上のM理論
  • モジュライ場の相互作用
  • Calabi-Yau four-fold上のF理論
• type IIB理論におけるフラックスコンパクト化
  • ノーゴー定理
  • フラックスにより誘導されるスーパー・ポテンシャル
  • 例：conifold上のフラックス背景
  • ワープした時空とゲージ階層

フラックスコンパクト化とCalabi-Yau four-folds

従来の弦理論では，非コンパクトな時空次元が4未満となるコンパクト化はあまり重要視されていなかった．これは，現実世界が4次元であるためである．しかし，この状況は弦の双対性の発見によって変化した．特に，この節で議論するM理論の共形Calabi-Yau four-fold上でのコンパクト化が，4次元への特定のF-理論コンパクト化と密接に関連していることが明らかになった．3次元理論は $\mathcal{N}=2$ 超対称性（保存される超電荷が4つ）を持つため，$\mathcal{N}=1$ 超対称性を持つ4次元理論と非常によく似ている．

演習で議論したように，グローバルな $\mathcal{N}=1$ 超対称性を持つ理論の超対称解は，運動方程式の零エネルギー解である．一次の超対称性制約を解くことで，二次の運動方程式の解が得られ，これにより一貫した弦理論の背景が構築できる．ただし，局所超対称性を持つ理論に一般化する際には注意が必要であり，Killingスピノル方程式を解くだけでは，必ずしも運動方程式の解になるとは限らない．この節では，フラックスコンパクト化における超対称性制約とBianchi恒等式を組み合わせることで，モジュライのポテンシャルから導かれる運動方程式の解が得られ，このポテンシャルがモジュライの安定化を記述することを示す．

Calabi-Yau four-fold上のM理論

11次元超重力のボソニック部分の作用は， $$ 2\kappa_{11}^2S=\int d^{11}x \sqrt{-G}\left( R-\frac{1}{2}|F_4|^2 \right)-\frac{1}{6}\int A_3 \wedge F_4 \wedge F_4 $$ である．フェルミオン場はグラビティーノのみであり，超対称な構成はKillingスピノル方程式 $$ \delta \Psi_M = \nabla_M \varepsilon + \frac{1}{12}(\Gamma_M\bm{F}^{(4)}-3\bm{F}_M^{(4)})\varepsilon = 0 $$ の非自明な解となる．記法は以前と同じです．この方程式を非自明なスピノル$\varepsilon$について解く必要があり，背景計量や4形式場の強さに制約を与える．以前，ヘテロティック弦の超対称性制約についても同様の解析を行ったが，そこでは3-形式テンソル場は簡単のためゼロとした．

一般に，追加の単純化仮定（または縮約）を行わない限り，フラックスをゼロに設定することは一貫していない．この節では，作用への量子補正の効果により，ほとんどのM理論の8次元多様体上のコンパクト化ではフラックスがゼロであることが一貫しないことを示す．

ここでは，$N=2$超対称性を保存するM理論の3次元Minkowski時空へのフラックスコンパクト化を構成する．3次元時空の最大対称性とPoincaré不変性に適合する最も一般的な計量のアンザッツは，ワープした計量である．これは，時空が外部時空と内部多様体の直積ではなく，内部次元の座標 $y$ に依存するスカラー関数（ワープ因子）$\Delta(y)$ が含まれることを意味する．計量アンザッツの明示的な形は $$ ds^2 = \Delta(y)^{-1} \underbrace{\eta_{\mu\nu} dx^{\mu}dx^{\nu}}{\text{3次元フラット時空}}+\Delta(y)^{1/2}\underbrace{g_{mn}(y) dy^m dy^n}{\text{8次元内部多様体}} $$ である．ここで $x$ は3次元Minkowski時空 $M_3$ の座標，$y^m$ は内部Euclid8次元多様体 $M$ の座標である．以下では，内部多様体がCalabi-Yau four-foldの場合を考え，これにより3次元で$N=2$超対称性が得られる．スカラー関数$\Delta(y)$はワープ因子と呼ばれる．式におけるワープ因子のべきは，後の議論の都合で選ばれている．

一般に，ワープ因子は幾何学の性質に劇的な影響を与えることがある．例えば，トーラスの場合を考えると，これは次のようなフラットな計量で記述できる： $$ ds^2 = d\theta^2 + d\varphi^2 \quad \text{with } 0 \leq \theta \leq \pi, \quad 0 \leq \varphi \leq 2\pi $$ 適切なワープ因子を導入すると，トーラスは球面へと変化する： $$ ds^2 = d\theta^2 + \sin^2\theta\, d\varphi^2 $$ これはトポロジーの変化をもたらす．さらに，ワープ因子が含まれると，時空が外部と内部成分に分離するとは限らなくなる．しかし，本節では（Calabi-Yau four-fold上のM理論のフラックスコンパクト化の場合），ワープ因子の効果はfour-foldのサイズが十分大きい領域ではサブリーディングとなることを示す．この領域では，前に議論したCalabi-Yau多様体の性質を利用できる．

上式の次元縮約を計算するためには，11次元のDirac行列を分解する必要がある．$11 = 3 + 8$ の分割に対して必要な分解は $$ \Gamma_{\mu}=\Delta^{-1/2}(\gamma_{\mu}\otimes \gamma_9) \quad \text{and} \quad \Gamma_m=\Delta^{1/4}(1\otimes \gamma_m) $$ である．ここで，$\gamma_{\mu}$は$M_3$の$2\times2$ディラック行列であり，具体的には $$ \gamma_0=i\sigma_1, \quad \gamma_1=\sigma_2, \quad \gamma_2=\sigma_3 $$ となる．$\sigma_i$はPauli行列であり， $$ \sigma_1=\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \quad \sigma_2=\begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}, \quad \sigma_3=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} $$ である．さらに，$\gamma_m$は$M$の$16\times16$ガンマ行列であり，$\gamma_9$は8次元のカイラリティ演算子で，$\gamma_9^2=1$を満たし，他の8つの$\gamma_m$と反可換である．$\gamma_m$と$\gamma_9$を実対称行列として表すことが可能かつ便利である．接空間基底では，内部空間$M$上の8つの$16\times16$Dirac行列を \begin{align} & \sigma_2 \otimes \sigma_2 \otimes 1 \otimes \sigma_{1,3} & & \sigma_2 \otimes \sigma_{1,3} \otimes \sigma_2 \otimes 1 \\ & \sigma_2 \otimes 1 \otimes \sigma_{1,3} \otimes \sigma_2 & & \sigma_{1,3} \otimes 1 \otimes 1 \otimes 1 \end{align} のように選ぶことができる．これら8つ全てと反可換な9番目の対称行列を $$ \gamma_9=\gamma_1\cdots\gamma_8=\sigma_2\otimes \sigma_2 \otimes \sigma_2 \otimes \sigma_2 $$ と定義できる．これからカイラリティ射影演算子 $$ P_{\pm}=\frac{1}{2}(1\pm \gamma_9) $$ を構成できる．

11次元のマヨラナスピノル$\varepsilon$は，次のような2項の和に分解される： $$ \varepsilon(x,y)=\zeta(x)\otimes\eta(y)+\zeta^*(x)\otimes\eta^*(y) $$ ここで$\zeta(x)$は3次元の2成分反可換スピノル，$\eta(y)$は8次元の16成分可換スピノルである．3次元で$N=2$超対称性を持つ理論では，内部空間$M$上に2つの線形独立なマヨラナ・ウェイルスピノル$\eta_1, \eta_2$が存在し，これらは上式の複素スピノルにまとめられている．一般には，この2つのスピノルは同じカイラリティである必要はない．しかし，Calabi-Yau four-foldの場合，内部多様体上のスピノルは複素ウェイル型となり， $$ \eta=\eta_1+i\eta_2 \quad \text{with} \quad (\gamma_9-1)\eta=0 $$ ここで$\gamma_9$の符号選択は慣習であり，正のカイラリティと呼ばれる．この2つの実スピノル$\eta_1, \eta_2$は，Spin(8)の表現$\bm{8}_c$をCalabi-Yau four-foldのホロノミー群$SU(4)$に分解したときの2つのシングレットに対応する： $$ \bm{8}_c \to \bm{6} \oplus \bm{1} \oplus \bm{1} $$

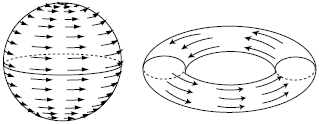
もし $\eta_1$ と $\eta_2$ が逆のカイラリティを持つ場合，複素スピノル $\eta = \eta_1 + i\eta_2$ は非カイラルとなる．逆カイラリティの2つのスピノルは，内部多様体上のベクトル場を定義する： $$ v_a = \eta_1^{\dagger} \gamma_a \eta_2 $$ このベクトルが消えないことを要求すると，興味深いクラスの解が得られる．実際，代数的位相幾何学のPoincaré–Hopf指数定理によれば，連続ベクトル場の零点の数は，背景幾何学のEuler数 $\chi$ の絶対値以上でなければならない．したがって，零点のないベクトル場が存在するのは，$\chi = 0$ の多様体のみである．この定理の例は図に示されている．M5-braneが3次元時空を満たし，内部空間の超対称な3サイクルを巻くようなフラックス背景は，このタイプの幾何学の例である．さらに，スピノルが非カイラルになると，AdS$_3$空間へのコンパクト化が可能となる．AdS空間へのコンパクト化は後で扱うため，本節の議論は正カイラリティのスピノルに限定する．この場合，AdS$_3$は解にならないことが分かる．

上式から導かれる制約は，計量のワープ因子依存性によって影響を受ける．前に述べたように，スピノルの共変微分は，共形変換で異なる2つの計量に対して関係がある．特に本ケースでは，内部成分と外部成分の計量がワープ因子の異なるべき乗で再スケールされ，vielbeinは $E_\mu = \Delta^{-1/2} e_\mu$ および $E_m = \Delta^{1/4} e_m$ となる．これにより次のようになる： \begin{align} \nabla_\mu \varepsilon \to& \nabla_{\mu}\varepsilon-\frac{1}{4}\Delta^{-7/4}(\gamma_{\mu} \otimes \gamma_9\gamma^m)\partial_m\Delta\varepsilon \\ \nabla_m \varepsilon \to& \nabla_{m}\varepsilon+\frac{1}{8}\Delta^{-1}\partial_n\Delta(1\otimes\gamma_m{}^n)\varepsilon \end{align} 最大対称な3次元時空へのコンパクト化では，Poincaré不変性によって $F_4$ の非ゼロ成分は $$ F_{mnpq}(y) \quad \text{と} \quad F_{\mu\nu\rho m}=\varepsilon_{\mu\nu\rho}f_m(y) $$ に制限される．ここで $\varepsilon_{\mu\nu\rho}$ は $M_3$ の完全反対称Levi-Civitaテンソルである．ガンマ行列を式(10.8)のように分解すると，非ゼロのフラックス成分は次の形になる： \begin{align} \bm{F}^{(4)} =& \Delta^{-1}(1\otimes\bm{F})+\Delta^{5/4}(1\otimes\gamma_9\bm{f}) \\ \bm{F}_{\mu}^{(4)} =& \Delta^{3/4}(\gamma_{\mu}\otimes\bm{f}) \\ \bm{F}_m^{(4)} =& -\Delta^{3/2}f_m(y)(1\otimes\gamma_9)+\Delta^{-3/4}(1\otimes\bm{F}_m) \end{align} ここで $F$, $F_m$, $f$ は10次元の場合と同様に定義されるが，テンソル場は8次元ディラック行列で縮約される： $$ \bm{F}=\frac{1}{24}F_{mnpq}\gamma^{mnpq},\quad \bm{F}_m=\frac{1}{6}F_{mnpq}\gamma^{npq}, \quad \bm{f}=\gamma^mf_m $$ 重力子の超対称性変換式は，添字 $M$ の値によって外部成分と内部成分に分かれる．

まず外部成分 $\delta \Psi_\mu = 0$ を解析しよう．3次元Minkowski時空では，共変的に定数なスピノル $$ \nabla_{\mu}\zeta=0 $$ を見つけることができる．その結果，$\delta \Psi_\mu = 0$ 方程式は $$ \partial\Delta^{-3/2}\eta+\bm{f}\eta+\frac{1}{2}\Delta^{-9/4}\bm{F}\eta=0 $$ となる．この式を射影演算子 $P_\pm$ を使って2つのカイラリティに射影すると， $$ \bm{F}\eta=0 $$ および $$ f_m(y)=-\partial_m\Delta^{-3/2} $$ が得られる．最後の式は，外部フラックス成分とワープ因子の関係を与える．

ガンマ行列とフラックスをそれぞれ分解した後，超対称性変換の内部成分 $\delta \Psi_m = 0$ は次の形になる： $$ \nabla_m\eta+\frac{1}{4}\Delta^{-1}\partial_m\Delta\eta-\frac{1}{4}\Delta^{-3/4}\bm{F}_m\eta=0 $$ この方程式から $$ \bm{F}_m\xi=0 \quad \text{および} \quad \nabla_m\xi=0 $$ が導かれる．ただし $$ \xi=\Delta^{1/4}\eta $$ である．$\xi$ はカイラリティが定まった消えない共変的に定数な複素スピノルなので，上式の2つ目の式は内部多様体 $M$ が共形的Calabi-Yau four-foldであることを意味する．

Calabi-Yau four-foldの数学的性質は，前に議論したthree-foldの場合と類似している．式に現れる共変的に定数なスピノルは，内部多様体のほぼ複素構造を定義するために用いることができる： $$ J_a{}^b = -i\xi^{\dagger}\gamma_a{}^b \xi $$ この構造はCalabi-Yau three-foldの場合と同じ性質を持つことを，演習で確認するよう求められている．Kähler多様体のDirac代数 $$ \{\gamma^a,\gamma^b\}=0,\quad \{\gamma^{\bar{a}},\gamma^{\bar{b}}\}=0, \quad \{ \gamma^a,\gamma^{\bar{b}} \}=2g^{a\bar{b}} $$ は，生成消滅演算子の代数として解釈できる．これは式の解を評価する際に有用である．これを理解するために，式を書き換えると $$ J_{a\bar{b}}=ig_{a\bar{b}}=-i\xi^{\dagger}\gamma_{a\bar{b}}\xi=-i\xi^{\dagger}(\gamma_a\gamma_{\bar{b}}-g_{a\bar{b}})\xi $$ となる．これから $$ 0=\xi^{\dagger}\gamma_a\gamma_{\bar{b}}\xi=(\gamma_{\bar{a}}\xi)^{\dagger}(\gamma_{\bar{b}}\xi) $$ が導かれる．ここで$a=b$とすると，$\xi$は$\gamma_{\bar{a}}$によって消される最高ウェイト状態であることが分かる： $$ \gamma_{\bar{a}}\xi=\gamma^a\xi=0 $$ これはCalabi-Yau four-foldの全ての添字について成り立つ．この結果を用いると，演習より式の最初の条件は以下のフラックス成分の消失を意味する： $$ F^{4,0}=F^{0,4}=F^{1,3}=F^{3,1}=0 $$ そして唯一非ゼロとなる成分は$F \in H(2,2)$であり，次のプリミティブ条件を満たす必要がある： $$ F_{a\bar{b}c\bar{d}}g^{cd}=0 $$ $\xi$が定まったカイラリティを持つため，$F$はCalabi-Yau four-fold上で自己双対となる．自己双対性から，式は次の形で書ける[5]： $$ F^{2,2}\wedge J=0 $$ 以上の解析の結果，$F$がプリミティブな(2,2)コホモロジーに属する場合，超対称性は破れない．すなわち， $$ F\in H_{\text{primitive}}^{(2,2)}(M) $$ 以下では，プリミティブ形式の一般的な定義と，完全なde Rhamコホモロジー構築におけるその重要性について議論する．

任意のKähler多様体の調和な$(p, q)$-形式は，プリミティブ形式のみを用いて完全に表現できる．この表現はLefschetz分解と呼ばれる．Lefschetz分解の構成は，角運動量状態 $|j, m\rangle$ を昇降演算子 $J_\pm$ で構築するFock空間の構成と非常によく似ている．第9章では，コンパクトKähler多様体のde RhamコホモロジーのHodge分解について議論した．Lefschetz分解はHodge分解と両立しており，以下でその関係を示す．

コンパクトKähler多様体 $M$（複素次元 $d$，実次元 $2d$）とKähler形式 $J$ に対して，調和形式（したがってde Rhamコホモロジー）上にSU(2)作用を定義できる．具体的には， \begin{align} &J_3 :& G \to& \frac{1}{2}(d-n)G \\ &J_- :& G \to& J\wedge G \\ &J_+ :& G \to& \frac{1}{2(n-2)!}J^{p_1p_2}G_{p_1p_2\cdots p_n}dx^{p_3}\wedge\cdots\wedge dx^{p_n} \end{align} ここで $G$ は調和な $n$-形式である．$J_-$ は $J_3$ の固有値を1だけ下げるので降下演算子として働き，$J_+$ は $J_3$ の値を1だけ上げるので昇降演算子として働く．問題では，これらの演算子がSU(2)代数を満たすことを確認するよう求められている．

角運動量代数の場合と同様に，調和形式の空間は $J_3$ および $J_2$ の固有値によって分類でき，基底状態は $$ |j,m \rangle \quad \text{with} \quad m=-j, -j+1, \ldots, j-1, j $$ で表される．プリミティブ形式は昇降演算子 $J_+$ で消される最高ウェイト状態として定義され， $$ J_+G_{\text{primitive}}=0 $$ となり，$|j,j\rangle$ のように表記できる．他の全ての状態（または調和形式）は，降下演算子 $J_-$ をプリミティブ形式に作用させることで得られる．プリミティブな $n$-形式はさらに $$ J_-^{2j+1}G_{\text{primitive}}=0 \quad \text{where} \quad j=\frac{d-n}{2} $$ を満たす．特に，中間次元コホモロジー（$n=d$ の場合）のプリミティブ形式は $j=0$ となり，これは $|0,0\rangle$ のシングレットであり，昇降演算子の両方で消される： $$ J_+G=0 \quad \text{or} \quad J_-G=0 $$ これら2つの式はそれぞれ式(10.35)と(10.36)に対応する．この議論から，プリミティブ形式を用いて任意の調和形式，すなわち全ての de Rham コホモロジー類の代表を構成できることが明らかである．概略的には，Lefschetz分解は $$ H^n(M)=\bigoplus_{k}J_-^k H_{\text{primitive}}^{n-2k}(M) $$ で与えられる[6]．

Lefschetz分解はHodge分解と両立しており，次のようにも書ける： $$ H^{(p,q)}(M)=\bigoplus_{k}J_-^k H_{\text{primitive}}^{(p-k,q-k)}(M) $$ このようにして，任意の調和な$(p, q)$-形式はプリミティブ形式で表すことができる．$M$がCalabi-Yau four-foldの場合，式よりプリミティブな$(p, q)$-形式は $$ \underbrace{J\wedge\cdots\wedge J}_{5-p-q}\wedge F_{\text{primitive}}^{p,q}=0 $$ を満たす．Calabi-Yau four-foldの場合，Hodgeスター演算子はプリミティブな$(p, 4-p)$コホモロジー上で固有値$(-1)^p$を持つ．この事実は後で重要となる．

未破れの超対称性を維持するためには，内部フラックス成分 $F_{mnpq}(y)$ がプリミティブな $(2,2)$-形式で与えられ，外部フラックス成分 $f_m(y)$ はワープ因子によって上式のように決定されることが分かった．ワープ因子を決定する方程式は，4形式場の強さの運動方程式から導かれる．自己双対性を用いると，エネルギー密度 $|F_4|^2$ は $\log \Delta$ のラプラシアンに比例し，これは内部多様体上で積分するとゼロになる．もしこれだけが全てであれば，フラックスは消失し，結局前に議論した通常のCalabi-Yauコンパクト化しか残らないことになる．しかし，11次元超重力への量子重力補正を考慮する必要があり，その場合，整合性のために非ゼロのフラックスが必要となる．この仕組みについて以下で説明する．

11次元超重力の作用には，リーマンテンソルの4次式である8形式 $X_8$ から生じる量子補正 $\delta S$ が加わる： $$ \delta S = -T_{M2} \int_M A_3 \wedge X_8 $$ ここで $$ X_8 = \frac{1}{(2\pi)^4} \left[ \frac{1}{192} \mathrm{tr} R^4 - \frac{1}{768} (\mathrm{tr} R^2)^2 \right] $$ この補正項は，IIA型弦理論における4つの重力子 $G_{\mu\nu}$ と1つの2形式テンソル場 $B_{\mu\nu}$ を含むワンループ散乱振幅を考察することで初めて導かれた．IIA型理論では，補正項はM理論の場合と同様の形をとり，3形式 $A_3$ がNS-NS 2形式 $B_2$ に置き換わる．結果がディラトンに依存しないため，M理論へ持ち上げることができる．

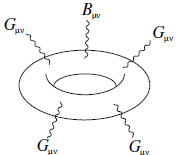
この $S$ 項は，11次元時空の境界上のアノマリーを打ち消すためにも必要である．例えば，強結合 $E_8 \times E_8$ 理論（ヘテロティック M理論としても知られる）ではこのような境界が現れる．この点については第5章で議論した．元々の $\int A_3 \wedge F_4 \wedge F_4$ 項と合わせて，理論の完全なChern-Simons項となり，単なる展開の先頭項ではない．実際，大きな体積極限で本質的に寄与する高次微分項はこれだけである．

場の強さはBianchi恒等式を満たす： $$ dF=0 $$ さらに，$\delta S$項は11次元の4形式場の運動方程式に寄与する．式を組み合わせると， $$ d\star F_4=-\frac{1}{2}F_4\wedge F_4-2\kappa_{11}^2T_{M2}X_8 $$ 式を用いると，ワープ因子に対する方程式が得られる： $$ d\star_8 d\log\Delta=\frac{1}{3}F\wedge F+\frac{4}{3}\kappa_{11}^2T_{M2}X_8 $$ この式を内部多様体上で積分すると，タッドポールキャンセル条件が導かれる．左辺の積分は正確な微分なので消え，ここではデルタ関数特異点（空間を満たすM2-brane）がないと仮定する．$X_8$の積分結果を得るには，異常特性類$X_8$を内部多様体の第1・第2ポントリャーギン形式で表すと便利である： $$ P_1=\frac{1}{(2\pi)^2}\left( -\frac{1}{2}\mathrm{tr}R^2 \right) \quad \text{and} \quad P_2=\frac{1}{(2\pi)^4}\left( -\frac{1}{4}\mathrm{tr}R^4 + \frac{1}{8}(\mathrm{tr}R^2)^2 \right) $$ これより $$ X_8=\frac{1}{192}(P_1^2-4P_2) $$ 複素多様体の場合，ポントリャーギン類はChern類と次のように関係する： $$ P_1=c_1^2-2c_2 \quad \text{and} \quad P_2=c_2^2-2c_1c_3+2c_4 $$ よって $$ X_8=\frac{1}{192}\left( c_1^4-4c_1^2c_2+8c_1c_3-8c_4 \right) $$ Calabi-Yau多様体では第1Chern類が消えるため，唯一非自明な寄与は第4Chern類から生じる．これはEuler数$\chi$と関係し， $$ \int_MX_8=-\frac{1}{24}\int_Mc_4=-\frac{\chi}{24} $$ したがって，式(10.50)からタッドポールキャンセル条件が得られる： $$ \frac{1}{4\kappa_{11}^2T_{M2}}\int_M F\wedge F=\frac{\chi}{24} $$

最後の式を用いることで，内部フラックス成分のおおよそのオーダーを見積もることができる．$\kappa_{11}^2$ と M2-brane のテンションを 11 次元プランク長 $\ell_p$ で表すと， $$ 4\kappa_{11}^2T_{M2}=2(2\pi\ell_p)^6 $$ となる．したがって，フラックスのオーダーは $$ F_{mnpq}\simeq \mathcal{O}\left(\frac{\ell_p^3}{\sqrt{v}}\right) $$ となる．ここで $v$ は Calabi-Yau four-fold の体積である．この結果を上式と比較すると，ワープ因子は $\log \Delta \sim \ell_p^6/v^{3/4}$ を満たし，もしこれが小さい場合， $$ \Delta \simeq 1+\mathcal{O}\left(\frac{\ell_p^6}{v^{3/4}}\right) $$ となる．Calabi-Yau のサイズが非常に大きい極限（すなわち $\ell_p/v^{1/8} \to 0$）では，背景計量はワープしないものとなる．

この解析から，M2-braneやM5-braneのデルタ関数的なソースが明示的に存在しなくても，非自明なフラックス解が可能であることが分かる．これは，F4の運動方程式やBianchi恒等式に現れる．非常によく似た状況は通常のマクスウェル理論にも現れ，磁気モノポールが存在しなくても，ループを流れる電流によって磁気フラックスが生成される．

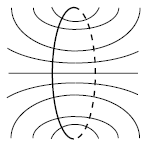
上式によれば，ワープ因子や背景幾何学に対して，明示的なブレーンソースが存在しなくても非特異な解が可能である．実際，空間全域で超重力近似の妥当性を厳密に正当化するためには，非特異な背景が必要となる．それでも，デルタ関数的な特異点を慎重に扱えば，特異な解に対しても超重力近似は有効である．

外部Minkowski空間を満たすM2-braneも存在する場合，式の左辺に追加の整数$N$（M2-braneの数）が現れ，次のようになる： $$ N+\frac{1}{4\kappa_{11}^2T_{M2}}\int_M F\wedge F=\frac{\chi}{24} $$ $F$が自己双対であるため，この式の左辺の両項は正である．したがって$\chi>0$の場合，非ゼロのフラックスやM2-braneを持つ超対称性保存解が存在する．このような解の数は，後で議論されるフラックスの量子化条件によって有限となる．一方，$\chi< 0$の場合，超対称性保存解は存在しない．

モジュライ場の相互作用

前に議論したように，Calabi-Yau four-fold には3つの独立なHodge数（$h_{1,1}$，$h_{2,1}$，$h_{3,1}$）があり，それぞれが低次元理論に現れるスカラー場の多重度を与える．本節の目的は，これらの多くの場がフラックスによって安定化できることを示すことである．

Calabi-Yau four-foldの複素構造の変動は，$h_{3,1}$個の複素パラメータ $T^I$ で記述され，これらは複素構造モジュライ場であり，カイラル超多重項に属する．Kähler構造の変形は，$h_{1,1}$個の実モジュライ $K^A$ を生じる．したがって，Kähler形式は $$ J=\sum_{A=1}^{h^{1,1}}K^A e_A $$ で与えられる．ここで $e_A$ は調和な (1,1)-形式の基底である．さらに，三形式 $A_3$ から生じる $h_{1,1}$個のベクトルと合わせて，$h_{1,1}$個の三次元ベクトル超多重項が得られる．加えて，三形式 $A_3$ から $h_{2,1}$個の追加の複素モジュライ $N^I$ が現れ，これらもカイラル超多重項に属する．議論を簡単にするため，以下ではスカラー $N^I$ は無視する．上述した三次元で未破れの $N=2$ 超対称性の条件は，いくつかのスカラー場がフラックスによって決定される条件として解釈できる．そこで，これらの条件を満たす三次元の相互作用を導出する．より直接的な導出は，Kaluza-Kleinコンパクト化に基づき，後で与えられる．

フラックスが存在しない場合，ベクトル多重項をカイラル多重項に置き換える双対変換を行うことができる．特に，ベクトル場はスカラー場に置き換えられる．この変換を行うと，Kählerモジュライは複素化される．フラックスが存在する場合，非自明なChern-Simons項が現れる．それでも双対変換は可能だが，より複雑になる．したがって，ここでは実Kählerモジュライで議論を進める．

複素構造モジュライ $T^I$ はカイラル多重項に現れ，それらを安定化する相互作用はスーパー・ポテンシャル $$ W^{3,1}(T)=\frac{1}{2\pi}\int_M \Omega \wedge F $$ によって記述される．ここで $\Omega$ はCalabi-Yau four-foldの正則4形式であり，$\kappa_{11}=1$とした．式を導く方法はいくつかあるが，最も簡単なのはこのスーパー・ポテンシャルが超対称性制約式を導くことを直接確認する方法である．別の導出は後で示されており，そこでは式がM理論を共形的Calabi-Yau four-fold上でKaluza-Kleinコンパクト化することで得られることが示されている．

宇宙定数がゼロの時空では，未破れの超対称性の条件はスーパー・ポテンシャルの消失と，スーパー・ポテンシャルのKähler共変微分の消失である．すなわち， $$ W^{3,1}=\mathcal{D}_IW^{3,1}=0 \quad \text{with} \quad I=1,\ldots,h_{3,1} $$ ここで $\mathcal{D}_I W^{3,1} = \partial_I W^{3,1} - W^{3,1} \partial_I \mathcal{K}^{3,1}$ であり，$\mathcal{K}^{3,1}$ は複素構造モジュライ空間上のKählerポテンシャルである（前に導入）．具体的には $$ \mathcal{K}^{3,1}=-\log\left(\int_M\Omega\wedge\bar{\Omega}\right) $$ Kählerポテンシャルは，これまで前に用いた3-形式ではなく，正則な四形式で定式化されている．条件 $W^{3,1}=0$ から $$ F^{4,0}=F^{0,4}=0 $$ が導かれる．three-foldの場合と同様に，$\partial_I$ は $(3,1)$ コホモロジーを生成するので，式の2つ目の条件は $$ F^{1,3}=F^{3,1}=0 $$ という制約を課す．式のスーパー・ポテンシャルの形は，スーパー・ポテンシャルに関する標準的な非摂動修正定理により，摂動論の全次数で成り立つ．この定理は，$D=4$ の $\mathcal{N}=1$ 理論でよく知られているが，$D=3$ の $\mathcal{N}=2$ 理論にも成り立つ[7]．超対称性により，式のスーパー・ポテンシャルは複素構造モジュライ場に対するスカラーポテンシャルを生成し，これらの場が安定化される．このポテンシャルについては後で議論する．

プリミティブ条件 $$ F^{2,2}\wedge J=0 $$ はKählerモジュライを安定化する方程式である．この条件は，実ポテンシャル $$ W^{1,1}(K)=\int_M J\wedge J \wedge F $$ から導くことができる．ここで $J$ はKähler形式である．この相互作用は文献によってはスーパー・ポテンシャルと呼ばれることもあるが，正則関数ではないため，この名称はやや誤解を招く．超対称性は $$ W^{1,1}=\partial_AW^{1,1}=0 \quad \text{with} \quad A=1,\ldots,h_{1,1} $$ という制約を課し，これがプリミティブ条件につながる．後で，$W^{1,1}$ がCalabi-Yau four-fold上でコンパクト化したM理論のモジュライ場のスカラーポテンシャルに現れることが示される．

Calabi-Yau four-fold上のF理論

共形的Calabi-Yau four-fold上でのM理論コンパクト化は，特定のCalabi-Yau four-fold上でのF理論コンパクト化と双対であり，これによって4次元時空で$\mathcal{N}=1$超対称性が得られる．この双対的な定式化は，現象論的な観点からより魅力的である．関心のあるF理論の背景は，非摂動的なtype IIB背景であり，Calabi-Yau four-foldが楕円ファイバー構造を持つ場合である（前に議論した通り）．

より具体的には，関心のあるCalabi-Yau four-foldは局所的にCalabi-Yau three-foldとトーラスの積として記述できる[8]．上で導出した4形式フラックスの条件は，type IIB理論における3形式フラックスの条件に対応する．具体的には，F理論の4形式とtype IIBの3形式の関係は $$ F_4=\frac{1}{\tau-\bar{\tau}}(G_3^{\star}\wedge dz-G_3\wedge d\bar{z}) $$ で与えられる．ここで $$ dz=d\sigma_1+\tau d\sigma_2 $$ $\sigma_1, \sigma_2$はトーラスをパラメータ化する座標であり，$\tau$はその複素構造である．type IIB理論ではこの$\tau$はアクシオン-ディラトン場と同一視される．また，$G_3 = F_3 - \tau H_3$はtype IIBのR-RおよびNS-NS 3形式の組み合わせである．成分で書くと， \begin{align} F^{1,3} =& \frac{1}{\tau-\bar{\tau}}[(G_3^{\star})^{0,3}\wedge dz-(G_3)^{1,2}\wedge d\bar{z}] \\ F^{0,4} =& -\frac{1}{\tau-\bar{\tau}}(G_3)^{0,3}\wedge d\bar{z} \end{align} M理論の超対称性制約$F^{0,4}=F^{1,3}=0$を課すと，type IIBの3形式に対して $$ G_3\in H^{(2,1)} $$ という超対称性制約が得られ，$G_3$の他の成分は消える．次節で示すように，$h^{1,0}=0$のCalabi-Yau three-fold上の任意の調和な(2,1)-形式は自動的にプリミティブである．したがって，背景がEuler数の非ゼロなCalabi-Yau three-foldの場合はプリミティブ条件は自動的に満たされるが，そうでない場合は追加の制約として課す必要がある．

Calabi-Yau four-fold上でのM理論やF理論のコンパクト化の例は，文献で多数構築されている．最も単純な例は，M理論を$K3 \times K3$上でコンパクト化するものであり，これは3次元で$\mathcal{N}=4$超対称性を持つ理論を導く．他の例としては，$T^2 \times T^2 \times T^2 \times T^2$のオービフォールドが含まれる．

type IIB理論におけるフラックスコンパクト化

ワープしたコンパクト化に関するノーゴー定理は，摂動的弦理論において1980年代までさかのぼる．これらの議論は，弦理論の低エネルギー超重力近似に基づいており，ミンコフスキー時空やド・ジッター時空へのワープしたコンパクト化は不可能であると主張された．内部空間がコンパクトかつ非特異であり，ブレーンソースが含まれない場合，ワープ因子やフラックスは超重力近似の先頭次数では必然的に自明となる．このような定理は1990年代に再検討され，ブレーンや低エネルギー超重力作用への高次補正の寄与がよりよく理解されるようになった．これらの要素によってノーゴー定理を回避し，type IIB理論のワープしたコンパクト化を構築することが可能となった．以下でその詳細を説明する．

ノーゴー定理

ノーゴー定理は，type IIB理論を内部空間がコンパクトかつ非特異であり，ブレーンソースが含まれない場合にコンパクト化すると，ワープ因子やフラックスは超重力近似の先頭次数では必然的に自明となることを主張する．この節では，この結果がどのように導かれるかを示し，さらにソース（ブレーン）がある場合にはノーゴー定理が破れることも示す．類似のノーゴー定理として，$D=4$のド・ジッター時空へのコンパクト化は運動方程式を解かないことも知られている．

具体例として，type IIB理論をコンパクト多様体 $M$ 上で4次元ミンコフスキー時空 $M_4$ へワープしたコンパクト化を考える．type IIB理論の10次元低エネルギー有効作用は前に示した．アインシュタイン枠での形は $$ S=\frac{1}{2\kappa^2}\int d^{10}x\sqrt{-G}\left[ R-\frac{|\partial\tau|^2}{2(\mathrm{Im}\,\tau)}-\frac{|G_3|^2}{2\mathrm{Im}\,\tau}-\frac{|\tilde{F}_5|^2}{4} \right]+\frac{1}{8i\kappa^2}\int\frac{C_4\wedge G_3\wedge G_3^{\star}}{\mathrm{Im}\,\tau} $$ ここで $$ G_3=F_3-\tau H_3 $$ であり，$F_3 = dC_2$，$H_3 = dB_2$ である．R-Rスカラー $C_0$（時にアクシオンと呼ばれる）とディラトン $\Phi$ は複素アクシオン-ディラトン場 $$ \tau = C_0 + i e^{-\Phi} $$ にまとめられる．以前との記法の違いは，10次元ベクトル添字に $M,N$ を使う点のみである．同セクションで説明したように， $$ \tilde{F}_5 = \star_{10} \tilde{F}_5 $$ という制約を課す必要がある．ここで $\star_{10}$ は10次元のHodgeスター演算子である．$|G_3|^2$ の定義は $$ |G_3|^2 = \frac{1}{3!} G^{M_1N_1} G^{M_2N_2} G^{M_3N_3} G_{M_1M_2M_3} G_{N_1N_2N_3}^{\star} $$ である．

理論を4次元にコンパクト化するために，次のようなワープした計量のアンザッツを考える： $$ ds_{10}^2=\sum_{M,N=0}^{9}G_{MN}dx^{M}dx^{N}=e^{2A(y)}\eta_{\mu\nu}dx^{\mu}dx^{\nu}+e^{-2A}g_{mn}(y)dy^{m}dy^{n} $$ ここで $x$ は4次元Minkowski時空の座標，$y^m$ は内部空間 $M$ の局所座標である．Poincaré不変性から，ワープ因子 $A(y)$ は内部多様体の座標のみに依存することが許される．

Poincaré不変性とBianchi恒等式は，許されるフラックス成分を制限する．3-形式フラックス $G_3$ は内部空間 $M$ のみの成分を持つことができ，一方，自己双対な五形式フラックス $\tilde{F}_5$ は次の形をとる必要がある： $$ \tilde{F}_5=(1+\star_{10})d\alpha\wedge dx^0 \wedge dx^1 \wedge dx^2 \wedge dx^3 $$ ここで $\alpha(y)$ は内部座標の関数であり，後でワープ因子 $A(y)$ と関係することが分かる．

ノーゴー定理は，作用から導かれる運動方程式を用いて導かれる．10次元のアインシュタイン方程式は次の形で書ける： $$ R_{MN}=\kappa^2\left( T_{MN}-\frac{1}{8}G_{MN}T \right) $$ ここで $$ T_{MN}=-\frac{2}{\sqrt{-G}}\frac{\delta S}{\delta G^{MN}} $$ はエネルギー・運動量テンソルであり，$T$はそのトレースである．この方程式は外部成分（$\mu\nu$）と内部成分（$mn$）に分かれるが，混合成分は自明に消える．外部成分は次の形になる[10]： $$ R_{MN}=-\frac{1}{4}G_{MN}\left( \frac{1}{2\mathrm{Im}\,\tau}|G_3|^2+e^{-8A}|\partial\alpha|^2 \right)\quad M,N=0,1,2,3 $$ 計量を変換すると，ワープ因子をフラックスで決定する方程式が得られる： $$ \Delta A=\frac{e^{4A}}{8\mathrm{Im}\,\tau}|G_3|^2+\frac{1}{4}e^{-8A}|\partial\alpha|^2 $$ または同等に， $$ \Delta e^{4A}=\frac{e^{8A}}{2\mathrm{Im}\,\tau}|G_3|^2+e^{-4A}(|\partial\alpha|^2+|\partial e^{4A}|^2) $$ ノーゴー定理はこの方程式から簡単に導かれる．両辺を内部多様体$M$上で積分すると，左辺は全微分なので消える．一方，右辺は正定値項の和であり，各項がゼロでなければ消えない．結果として，$A$と$\alpha$は定数，$G_3$は消失することになる．最大対称性の仮定により，外部時空に宇宙定数$\Lambda$を許すこともできるが，$\Lambda < 0$ならAdS時空，$\Lambda>0$ならdS時空となる．上記ノーゴー定理はこの宇宙定数を含む場合にも一般化できる．問題で示すように，$\Lambda$は式の右辺に正の係数で現れる．同様の議論により，ソースや特異点がない場合，dS解を除外する別のノーゴー定理が得られる．

フラックスにより誘導されるスーパー・ポテンシャル

ブレーンソースが存在すると，ノーゴー定理は破れる場合があることが分かっている．これらのソースにはエネルギー・運動量テンソルが伴い，式の右辺に $$ 2\kappa^2 e^{2A} \mathcal{J}_{\text{loc}} $$ の形で寄与する．ここで $$ \mathcal{J}_{\text{loc}} = \frac{1}{4} \left( \sum_{M=5}^{9} T_M{}^M - \sum_{M=0}^{3} T_M{}^M \right)_{\text{loc}} $$ であり，$T_{\text{loc}}$は局所的なソースに対応するエネルギー・運動量テンソルである． $$ T_{MN}^{\text{loc}} = -\frac{2}{\sqrt{-G}} \frac{\delta S_{\text{loc}}}{\delta G^{MN}} $$ ここで$S_{\text{loc}}$はソースを記述する作用である．Dp-braneが内部空間$M$の$(p-3)$-サイクル$\Sigma$を巻く場合，関連する相互作用は $$ S_{\text{loc}} = -\int_{\mathbb{R}^4 \times \Sigma} d^{p+1}\xi\, T_p \sqrt{-g} + \mu_p \int_{\mathbb{R}^4 \times \Sigma} C_{p+1} $$ となる．これは$\alpha'$の先頭次数かつブレーン上のフラックスがゼロの場合の作用であり，詳細は前に説明されている．D7-braneが4サイクルを巻く場合には，D7-brane上のChern-Simons項による$\alpha'$補正 $$ -\mu_3 \int_{\mathbb{R}^4 \times \Sigma} C_4 \wedge \frac{p_1(R)}{48} $$ を含める必要がある．上式は，式の右辺に負の項を与える場合があることが分かっている．

これらのソースは，$\tilde{F}_5$ に対するBianchi恒等式にも寄与する[11]： $$ d\tilde{F}_5=H_3\wedge F_3+2\kappa^2T_3\rho_3 $$ ここで $\rho_3$ は局所化されたソースによるD3電荷密度であり，通常通り，ソースに沿ってデルタ関数因子を含む．

式を内部多様体 $M$ 上で積分すると，type IIB のタッドポールキャンセル条件が得られる： $$ \frac{1}{2\kappa^2T_3}\int_M H_3 \wedge F_3 + Q_3 = 0 $$ ここで $Q_3$ は $\rho_3$ に関連する全電荷である．その結果，非ゼロの $Q_3$ 電荷は三形式の期待値を誘導する．以下で $G_3$ が虚自己双対であることが示される．したがって，三形式フラックスは $Q_3$ が負の場合のみ誘導される．問題では，D7-brane が式の右辺に負の寄与を与えることを，ブレーンの存在下で運動方程式を解いて確認するよう求められている．

type IIB解を記述する有用な方法は，これをF理論の楕円ファイバー付きCalabi-Yau four-fold $X$ 上のコンパクト化へ持ち上げることである．前に説明したように，ファイバーのベースはtype IIBの幾何学を符号化し，ファイバー自体はtype IIBのアクシオン・ディラトン場 $\tau$ の振る舞いを記述する．この定式化では，タッドポールキャンセル条件はM理論のfour-foldの場合と類似の形になる： $$ \frac{\chi(X)}{24}=N_{D3}+\frac{1}{2\kappa^2T_3}\int_M H_3 \wedge F_3 $$ ここで $\chi(X)$ はfour-foldのEuler数，$N_{D3}$ はコンパクト化に含まれるD3-brane電荷である[12]．この式の左辺は，D7-braneの曲率によって誘導されるD3-brane電荷の負の値として解釈できる．したがって，この式は全てのソースからのD3-brane電荷が打ち消されるための条件である．

この背景はどのような条件を満たすのか？この問いに答える方法はいくつかある．1つは，先に述べた運動方程式を，今度はブレーンソースを考慮して解くことである．概略的には，式の$\tilde{F}_5$フラックスを式のBianchi恒等式に代入し，その結果を式の縮約されたEinstein方程式から差し引き，ブレーンソースによるエネルギー・運動量テンソルの寄与を考慮する．得られる制約は次の通り： $$ \Delta (e^{4A}-\alpha) =& \frac{1}{6\mathrm{Im}\,\tau}e^{8A}|iG_3-\star G_3|^2+e^{-4A}|\partial(e^{4A}-\alpha)|^2+2\kappa^2e^{2A}(\mathcal{J}_{\text{loc}}-T_3\rho_3^{\text{loc}}) $$ ほとんどの局所化されたソースは，BPS型の束縛条件 $$ \mathcal{J}_{\text{loc}} \geq T_3\rho_3^{\text{loc}} $$ を満たす．

以上の結果から，ここで考察する種類のソースに対して，方程式の解は以下の条件で特徴付けられる：

• 3-形式場の強さ $G_3$ は虚自己双対である． $$ \star G_3 = iG_3 $$ ここで $\star$ は6次元でのHodge双対を表す．虚自己双対条件の解は，$(2,1)+(0,3)$型の調和形式である．以下で示すように，超対称性解では$(2,1)$成分のプリミティブ部分のみが許される．
• ワープ因子と四形式ポテンシャルの間に関係がある． $$ e^{4A} = \alpha $$
• ソースはBPS束縛を飽和する，すなわち $$ \mathcal{J}_{\text{loc}} = T_3\rho_3^{\text{loc}} $$ この式は，例えばD3-braneで満たされる．実際，D3-braneのワールドボリューム作用の関連項を用いると $$ T_0{}^0 = T_1{}^1 = T_2{}^2 = T_3{}^3 = -T_3\rho_3 \quad \text{and} \quad T_m{}^m = 0 $$ となる．これはBPS不等式が満たされるだけでなく，飽和されることを意味する．一方，反D3-braneは不等式は満たすが飽和しない．左辺は正のままだが，右辺は符号が逆になる．BPS束縛を飽和する別の方法として，4サイクルを巻くD7-braneやO3プレーンがある．崩壊する2サイクルを巻くD5-braneは不等式は満たすが，飽和はしない．

式の制約は，複素構造モジュライ場に対するスーパー・ポテンシャルから導くことができる： $$ W = \int_M \Omega \wedge G_3 $$ ここで $\Omega$ はCalabi-Yau three-foldの正則三形式である．

スーパー・ポテンシャルを用いて未破れの超対称性の条件を導出しよう．具体例として，Calabi-Yau多様体のサイズを特徴付ける唯一のKählerモジュライを持つ場合を考える．フラックスを導入する前は，複素構造モジュライ $z^\alpha$（$\alpha=1,\ldots,h_{2,1}$），アクシオン・ディラトン $\tau$，そしてKählerモジュライを含む超場 $\rho$ を記述する質量のない場が存在する．

演習で説明されているように，Kählerポテンシャルは，Calabi-Yau多様体のサイズを十分大きく取った場合の10次元type IIB作用の次元縮約から計算できる．ラジアルモジュラス$\rho$に対する結果は $$ \mathcal{K}(\rho)=-3\log[-i(\rho-\bar{\rho})] $$ これにアクシオン・ディラトンおよび複素構造モジュライに対する結果を加える必要がある．それらは $$ \mathcal{K}(\tau)=-\log[-i(\tau-\bar{\tau})] \quad \text{and} \quad \mathcal{K}(z^\alpha)=-\log\left(i\int_M \Omega \wedge \bar{\Omega}\right) $$ である．全体のKählerポテンシャルは $$ \mathcal{K} = \mathcal{K}(\rho) + \mathcal{K}(\tau) + \mathcal{K}(z^\alpha) $$ で与えられる．

超対称性が未破れであるための条件は $$ \mathcal{D}_{a}W=\partial_aW+\partial_a\mathcal{K}W=0 $$ ここで $a=\rho,\tau,\alpha$ は全てのモジュライ超場をラベルする．まず，式のスーパー・ポテンシャルはラジアルモジュラスに依存しないことに注意する．その結果， $$ \mathcal{D}_{\rho}W=\partial_{\rho}\mathcal{K}W=-\left( \frac{3}{\rho-\bar{\rho}} \right)W=0 $$ となり，超対称解は $$ W=0 $$ を満たす必要がある．したがって，$G_3$の$(0,3)$成分は消失しなければならない．さらに， $$ \mathcal{D}_{\tau}W=\frac{1}{\tau-\bar{\tau}}\int_M \Omega \wedge \bar{G}_3=0 $$ より，$G_3$の$(3,0)$成分も消失しなければならない．残りの条件は $$ \mathcal{D}_{\alpha}W=\int_M \chi_{\alpha} \wedge G_3 =0 $$ ここで $\chi_{\alpha}$ は前に導入した調和な$(2,1)$-形式の基底である．この条件が全ての調和な$(2,1)$-形式について成り立つため，超対称性が未破れであるためには $$ G_3 \in H^{(2,1)}(M) $$ でなければならない．

Euler数がゼロのコンパクトなCalabi-Yau three-foldでは $h^{1,0} = 0$ が成り立つ．この場合，任意の調和な$(2,1)$-形式はプリミティブである．これを確認するために，Lefschetz分解をこの場合に適用してみよう．調和な$(2,1)$-形式 $$ \chi=\frac{1}{2}\chi_{ab\bar{c}}dz^a \wedge dz^b \wedge d\bar{z}^{\bar{c}} $$ は，$J$に平行な部分と直交する部分に分解できる： $$ \chi=v\wedge J+(\chi-v\wedge J)=\chi_{\parallel}+\chi_{\perp} $$ ここで $$ v=\frac{3}{2}\chi_{ap\bar{q}}J^{p\bar{q}}dz^a $$ と定義し， $$ \chi_{\perp} \wedge J=0 $$ となるように選んでいる．一方，このような1-形式$v$が存在する場合，それは調和であり，これは$h^{1,0} \neq 0$を意味する．したがって，$\chi = \chi_{\perp}$ となり，任意の調和な$(2,1)$-形式はプリミティブである．調和な$(2,1)$-形式がプリミティブであることを証明するには，$h^{1,0}=0$が必要であることに注意しよう．六次元トーラスでは$h^{1,0} \neq 0$であり，プリミティブでない調和な$(2,1)$-形式も存在する．$h^{1,0} \neq 0$の場合，超対称性が未破れであるためには $$ G_3 \in H_{\text{primitive}}^{(2,1)} $$ でなければならない．プリミティブであることに加えて，$\chi$は虚自己双対でもある．三形式のHodgeスター作用に対する振る舞いは表にまとめられている．Levi-Civitaテンソルを $$ \varepsilon_{abc\bar{p}\bar{q}\bar{r}}=-i(g_{a\bar{p}}g_{b\bar{q}}g_{c\bar{r}}\pm \text{permutations}) $$ の形で表すと，演習の議論によりこれらの規則を確認できる．このとき，式は$G_3$が虚自己双対であるという条件と一致する．

例：conifold 上のフラックス背景

前に議論したように，異なるCalabi-Yau多様体はconifold遷移によって接続されている．接続点ではCalabi-Yau多様体が退化する．本節では，モジュライ空間のconifold特異点付近におけるCalabi-Yau多様体の挙動をさらに探る．これらの特異点を含めることで，多くの，場合によっては全てのCalabi-Yau多様体を単一の連結なウェブの一部として記述することが可能となる．これらの特異点を含めるためには，特異点をどのように滑らかにするかを理解する必要がある．これは「変形」と「解消」という2つの異なる方法で実現できる．

Conifold特異点は，コンパクトなCalabi-Yau空間のモジュライ空間によく現れるが，three-foldの特異点近傍を拡大して得られる非コンパクトCalabi-Yau空間で解析するのが最も便利である．この非コンパクトCalabi-Yau空間は「conifold」と呼ばれ，その幾何学は円錐で与えられる．この節では，conifoldの時空幾何学と，それを滑らかにした「変形conifold」や「解消conifold」について説明する．type IIB超弦理論を変形conifold上でコンパクト化することは，興味深いフラックスコンパクト化の例となる．これは閉じ込め型ゲージ理論の超弦理論的双対であり，第12章で詳しく説明される．ここでは超重力解析にとどめる．

コニフォールド点では，Calabi-Yau three-foldが円錐型の特異点を持つようになる．これは，$\mathbb{C}^4$内の二次方程式 $$ \sum_{A=1}^{4}(w^A)^2=0 \quad \text{for} \quad w^A \in \mathbb{C}^4 $$ で定義される超曲面として記述できる．この方程式は，$w^A=0$以外では滑らかな空間を表す．これは$S^2 \times S^3$を底とする円錐であることが分かる．実際，$w^A$がこの方程式を満たすなら，任意の複素定数$\lambda$に対して$\lambda w^A$も同じ方程式を満たすので，円錐構造となる．$w^A = x^A + i y^A$とし，新しい座標$\rho$を導入すると，上の方程式は次の3つの実方程式に書き換えられる： $$ \vec{x}\cdot\vec{x}-\frac{1}{2}\rho^2=0,\quad \vec{y}\cdot\vec{y}-\frac{1}{2}\rho^2=0,\quad \vec{x}\cdot\vec{y}=0 $$ 最初の式は半径$\rho/\sqrt{2}$の$S^3$を記述する．残り2つの式は，$S^3$上に$S^2$がファイバーされた構造と解釈できる．この空間上にはRicci平坦かつKählerな計量があり，円錐型の形 $$ ds^2=dr^2+r^2d\Sigma^2 $$ で与えられる．ここで$r=\sqrt{3/2}\,\rho^{2/3}$，$d\Sigma^2$は5次元の底空間の計量であり，トポロジーは$S^2 \times S^3$となる．底空間の計量は角変数で明示的に $$ d\Sigma^2=\frac{1}{9}\left( 2d\beta+\sum_{i=1}^{2}\cos\theta_id\phi_i \right)^2+\frac{1}{6}\sum_{i=1}^{2}(d\theta_i^2+\sin^2\theta_id\phi_i^2) $$ と書ける．角変数の範囲は $$ 0\leq\beta\leq 2\pi,\quad 0\leq\theta_i\leq\pi,\quad 0\leq\phi_i\leq 2\pi $$ （$i=1,2$）であり，$0 \leq r < \infty$である．この空間の等長群は$SU(2) \times SU(2) \times U(1)$である[13]．

この背景をより詳細に記述するためには，次の1-形式の基底を導入すると便利である： \begin{align} g^1 =& \frac{1}{\sqrt{2}}(e^1-e^3), & g^2 =& \frac{1}{\sqrt{2}}(e^2-e^4), \\ g^3 =& \frac{1}{\sqrt{2}}(e^1+e^3), & g^4 =& \frac{1}{\sqrt{2}}(e^2+e^4), \\ g^5 =& e^5 \end{align} ここで \begin{align} e^1 =& -\sin\theta_1d\phi_1, \quad e^2=d\theta_1 \\ e^3 =& \cos2\beta\sin\theta_2 d\phi_2-\sin2\beta d\theta_2 \\ e^4 =& \sin2\beta\sin\theta_2d\phi_2+\cos2\beta d\theta_2 \\ e^5 =& 2d\beta+\cos\theta_1d\phi_1+\cos\theta_2d\phi_2 \end{align} この基底を用いると，計量は次の形になる： $$ d\Sigma^2=\frac{1}{9}(g^5)^2+\frac{1}{6}\sum_{i=1}^{4}(g^i)^2 $$

コニフォールドは $r=0$ で円錐型の特異点を持つ．実際，これは単位半径の5次元球面以外の任意の5次元底空間を選んだ場合にも成り立つ．前述したように，コニフォールドの場合，円錐の先端の特異点を滑らかにする方法として「変形」と「解消」の2通りがある．

変形とは，式を $$ \sum_{A=1}^{4}(w^A)^2 = z $$ のように置き換えることである．ここで $z$ はゼロでない複素定数である．$w^A$（$A=1,\ldots,4$）は座標のスケール変換が可能なので，$z$は実数かつ非負と仮定できる．この方程式は，$z$の任意の値に対してCalabi-Yau three-foldを定義する．結果として，$z$は一次元のモジュライ空間を張る．モジュライ空間の特異点（$z=0$）では，多様体は特異（$\rho=0$）となる．

大きな $r$ では，変形コニフォールドの幾何学は $z=0$ の特異なコニフォールド，すなわち $S^2 \times S^3$ を底とする円錐に近づく．$r$ を原点に近づけると，$S^2$ と $S^3$ の両方が縮小する．$w^A$ を実部と虚部に分解すると，次のようになる： $$ z = \vec{x}\cdot\vec{x}-\vec{y}\cdot\vec{y} $$ さらに定義 $$ \rho^2=\vec{x}\cdot\vec{x}+\vec{y}\cdot\vec{y} $$ を用いると，$r$ の範囲は $$ z \leq \rho^2 < \infty $$ となる．したがって，$z>0$ の場合は原点の特異点が回避される．これは，$\rho^2$ が $z$ に近づくと $S^2$ が消失し，有限半径の $S^3$ のみが残ることを示している．

円錐型特異点を滑らかにする2つ目の方法は「解消」と呼ばれる．この場合，円錐の頂点に近づくと $S^3$ がゼロサイズまで縮小し，$S^2$ のサイズはゼロにならず有限のままである．この方法は「スモール解消」とも呼ばれ，得られる非特異な空間は「解消コニフォールド」と呼ばれる．

この仕組みを説明するために，線形変数変換を行い，特異なコニフォールドを次の形に書き換えよう： $$ \mathrm{det}\begin{pmatrix} X & U \\ V & Y \end{pmatrix} = 0 $$ $(X, Y, U, V) = 0$ 以外の点では，この空間は次の方程式で同等に記述できる： $$ \begin{pmatrix} X & U \\ V & Y \end{pmatrix} \begin{pmatrix} \lambda_1 \\ \lambda_2 \end{pmatrix} = 0 $$ ここで $\lambda_1$ と $\lambda_2$ が同時にゼロでないとする．$\lambda_i$ の解は全体のスケール変換（すなわち） $$ (\lambda_1,\lambda_2)\simeq \lambda(\lambda_1,\lambda_2) \quad \text{with} \quad \lambda\in\mathbb{C}^* $$ まで定まる．したがって，$(X, Y, U, V)$ と $(\lambda_1, \lambda_2)$ は $\mathbb{P}^1$ 上にあり，条件を満たす．この空間が「解消コニフォールド」であり，特異点が除去された非特異な空間となる．なぜ特異点が消えるのか？この問いに答えるために，$(X, Y, U, V) \neq (0, 0, 0, 0)$ の場合はこの空間が特異なコニフォールドと一致することに注意しよう．しかし，$(X, Y, U, V) = (0, 0, 0, 0)$ では，$(\lambda_1, \lambda_2)$ の任意の解が許される．この空間は $\mathbb{C}P^1$，すなわち2次元球面である．

ここで，conifold幾何学上のフラックス背景を考察する．具体的には，円錐の先端に位置するN個の時空を満たすD3-braneと，変形conifoldの底にある$S^2$を巻き，4次元時空を満たすM個のD5-brane（これらは通常「フラクショナルD3-brane」と呼ばれる）を配置する場合である．

この背景は，M個のD5-braneを配置することで構築できる．これらは $$ \int_{S^3}F_3=4\pi^2\alpha'M $$ を与える．この式は次のようにも書ける： $$ F_3=\frac{M\alpha'}{2}\omega_3 \quad \text{where} \quad \omega_3=g^5\wedge \omega_2 $$ ここで $$ \omega_2=\frac{1}{2}(\sin\theta_1d\theta_1\wedge d\phi_1-\sin\theta_2d\theta_2\wedge d\phi_2) $$ 超対称な背景を記述するためには，複素三形式$G_3$が虚自己双対な$(2,1)$-形式である必要がある．これにより$H_3$フラックスも含める必要がある．虚自己双対性から$H_3$フラックスは $$ H_3=\frac{3}{2r}g_sM\alpha'dr\wedge \omega_2 $$ で決まる．ここで$g_s = e^{\Phi}$は弦の結合定数（定数と仮定），アクシオン$C_0$はゼロとした．$H_3$と$F_3$がともに存在すると，Bianchi恒等式 $$ d\tilde{F}_5=H_3\wedge F_3+2\kappa^2T_3\rho_3 $$ により$F_5$は $$ \tilde{F}_5=(1+\star_{10})\mathcal{F} $$ で与えられる．ここで $$ \mathcal{F}=\frac{1}{2}\pi(\alpha')^2N_{\text{eff}}(r)\omega_2\wedge \omega_3 $$ かつ $$ N_{\text{eff}}(r)=N+\frac{3}{2\pi}g_sM^2\log\left(\frac{r}{r_0}\right) $$ となる．全体の五形式フラックスは半径$r$に依存し， $$ \int_{\Sigma}\tilde{F}_5=\frac{1}{2}(\alpha')^2\pi N_{\text{eff}}(r) $$ となることに注意しよう．

この場合の幾何学はワープしたコニフォールドであり，計量は次の形をしている： $$ ds_{10}^2 = e^{2A(r)}\eta_{\mu\nu}dx^{\mu}dx^{\nu} + e^{-2A(r)}(dr^2 + r^2 d\Sigma^2) $$ 底空間の計量 $d\Sigma^2$ は上式で与えられる．この座標系での体積要素は $$ \sqrt{-g} = \frac{1}{54} e^{-2A} r^5 \sin\theta_1 \sin\theta_2 $$ となる．これと $$ \omega_2 \wedge \omega_3 = -d\beta \wedge \sin\theta_1 d\theta_1 \wedge d\phi_1 \wedge \sin\theta_2 d\theta_2 \wedge d\phi_2 $$ を用いると， $$ \star(\omega_2 \wedge \omega_3) = 54 r^{-5} e^{8A} dr \wedge dx^0 \wedge dx^1 \wedge dx^2 \wedge dx^3 $$ となる．

ワープ因子は五形式フラックスによって上式で決定される．同等に $$ \star_{10}\mathcal{F}=d\alpha \wedge dx^0 \wedge dx^1 \wedge dx^2 \wedge dx^3 $$ となり，$\alpha = \exp(4A)$ である．五形式フラックスの式を用いると，次の方程式が得られる： $$ d\alpha=27\pi(\alpha')^2\alpha^2r^{-5}N_{\text{eff}}(r)dr $$ これを積分すると，ワープ因子は $$ e^{-4A(r)}=\frac{27\pi(\alpha')^2}{4r^4}\left[ g_sN+\frac{3}{2\pi}(g_sM)^2\log\left(\frac{r}{r_0}\right)+\frac{3}{8\pi}(g_sM)^2 \right] $$ となる．ここで $r_0$ は積分定数である．

問題では，$G_3$がプリミティブであることを示すよう求められている．この結果は，この背景が超対称的であることを意味する．なお，本節では，コンパクト空間に対して導出された式を用いているが，これらの制約はtype IIBのKillingスピノル方程式からも導出でき，局所的なものである．したがって，非コンパクト空間にも成り立つ．

ワープした時空とゲージ階層

Poincaré不変性が余剰次元を持つ時空に対してワープ積構造を許すという事実は，現象論に興味深い帰結をもたらす．ブレーンワールド・シナリオは，観測される4次元世界が5次元時空に埋め込まれたブレーンに閉じ込められているという提案に基づくトイモデルである[14]．この提案のあるバージョンでは，5番目の次元は巻き込まれておらず，無限に広がっている．もし我々がそのようなブレーン上に住んでいるなら，なぜ重力は5次元の逆三乗則ではなく，4次元のNewton的逆二乗則になるのか？その答えは，時空がワープしているためである．この仕組みについて詳しく見てみよう．

5次元重力と宇宙定数$\Lambda$，および3-braneの存在下での作用は $$ S \sim \int d^5x \sqrt{-G} (R-12\Lambda) -T\int d^4x \sqrt{-g} $$ で与えられる．ここで$T$は3-braneのテンション，$G_{MN}$は5次元計量，$g$はbrane上の誘導された4次元計量である．この作用は，運動方程式の解として $$ ds^2=e^{-2A(x_5)}\eta_{\mu\nu}dx^{\mu}dx^{\nu}+dx_5^2 $$ の形を許す．ここで $$ A(x_5)=\sqrt{-\Lambda}|x_5| $$ $-1 \leq x_5 \leq 1$は無限大まで広がっており，braneは$x_5=0$に位置する．さらに，静的解のためにはbraneのテンションが宇宙定数$\Lambda$と $$ T=12\sqrt{-\Lambda} $$ という関係を満たす必要があり，これは宇宙定数が負であることを要求する．この幾何学は局所的には反ド・ジッター空間（AdS$_5$）であるが，$x_5=0$で計量の微分に不連続性が現れる．この不連続性は，一般相対論の標準的なマッチング公式を用いてデルタ関数型のbraneソースによって決定される．

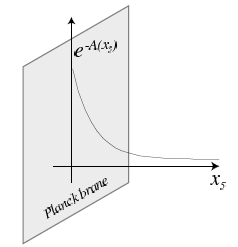
計量にはワープ因子が含まれており，これにより5次元が無限に広がっているにもかかわらず，ブレーン上では4次元の重力が観測されるという興味深い結果が生じる．このようにして余剰次元を隠す方法は，コンパクト化とは異なるアプローチである．この幾何学における5次元重力子の正規モードを計算すると，4次元重力子として解釈されるゼロモードがブレーン近傍に局在し，その相互作用は $G_4$ によって制御されることが分かる．ブレーン上の有効な4次元プランク質量は $$ M_4^2 = M_5^3 \int dx_5\, e^{-2\sqrt{-\Lambda}|x_5|} $$ で与えられ，ニュートン定数で表すと $$ G_4 = G_5 \left( \int dx_5\, e^{-2\sqrt{-\Lambda}|x_5|} \right)^{-1} $$ となる．

もし1つの3-braneではなく，2つの平行な3-braneを考えると，現象論への影響はさらに興味深いものとなる．この構成では，背景幾何学は再びワープ積構造を持つが，今度はワープ因子が階層問題を自然に解決する方法を提供する．

3-braneが再び5次元時空に埋め込まれていると仮定しよう．1つのbraneは$x_5 = r$に位置し，標準模型brane（SM）と呼ばれる．もう1つのbraneは$x_5 = 0$に位置し，プランクbrane（P）と呼ばれる．5次元重力が2つのbraneと結合した作用は $$ S=\int d^5x \sqrt{-G}(R-12\Lambda)-T_{\text{SM}}\int d^4x \sqrt{-g^{\text{SM}}}-T_{\text{P}}\int d^4x \sqrt{-g^{\text{P}}} $$ である．ここで$T_{\text{SM}}$と$T_{\text{P}}$は2つのbraneのテンションである．計量は再びワープ積構造を仮定する： $$ ds^2=e^{-2A(x_5)}\eta_{\mu\nu}dx^{\mu}dx^{\nu}+dx_5^2 $$ 区間$0 \leq x_5 \leq r$で定義される．

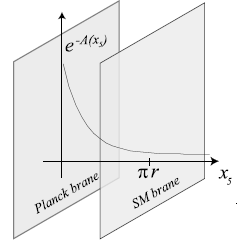
運動方程式は，ワープ因子 $$ A(x_5)=\sqrt{-\Lambda}|x_5| $$ によって解かれ， $$ T_{\text{P}}=-T_{\text{SM}}=12\sqrt{-\Lambda} $$ となる．負のテンションは一見不自然に思えるかもしれないが，負テンションブレーンはオリエンティフォールド模型やF理論コンパクト化で実現可能である．この解では，計量はプランクブレーン上で $$ g_{\mu\nu}^{\text{P}}=\eta_{\mu\nu} $$ となるように規格化されている．ワープ因子のため，SMブレーン上の計量は $$ g_{\mu\nu}^{\text{SM}}=e^{-2\pi r\sqrt{-\Lambda}}\eta_{\mu\nu} $$ となる．

このスケール因子は，プランク・ブレーン上でエネルギー $E$ を持つ物体が，SMブレーン上では赤方偏移して $e^{-r\pi\sqrt{-\Lambda}}E$ のエネルギーを持つ物体として観測されることを意味する．分離スケール $r$ を適切に選ぶことで，この因子を $10^{-16}$ 程度に調整し，プランク・ブレーン上の物理をSMブレーン上でTeVスケールの物理として実現できる．この提案（Randall-Sundrumによる）は，ゲージ階層問題の解決策として興味深いものである．このシナリオには多くの顕著な帰結がある．従来は超高エネルギースケールに限定されていた現象が，加速器エネルギーで観測可能になる可能性が生じる．したがって，Kaluza-Kleinモード，基本弦，ブラックホール，重力波などが全て観測可能となる．LHC実験では，これら全ての可能性を探索する準備が進められている．多くの人が発見される可能性が高いと考えている超対称性も，これと比べると平凡に見える．予想通り，これらのアイデアは大きな注目を集めており，関連する文献は急速に増加している．以下では，このシナリオが弦理論でどのように実現されるかについて簡単に概説する．

上記の階層問題の解決アプローチが弦理論に自然に現れるのは興味深いことである[15]．この目的に最も適していると思われるブレーンは，type IIBオリエンティフォールドやF理論構成におけるD3-braneである．コンパクトな内部多様体上の点にD3-braneを配置することが考えられる．大きな階層を得るには，2組のD3-braneを距離rだけ離して配置する必要があり，この距離rが階層の大きさを決定する．しかし，rは4次元理論ではモジュライであり，D3-braneの座標にはポテンシャルがない．以下では，このセクションの冒頭で議論したフラックス背景を用いることで，大きくかつ安定した階層を生み出すワープした背景が得られることを示す．

具体的には，変形コニフォールド幾何学を考えることができる．円錐の先端付近の局所的なフラックス解は，前節で説明したものと類似している．しかし，大域的には，背景解は変更する必要がある．ここではコンパクトな解に関心があるためである．前節で示したコニフォールド解は非コンパクトであり，rは無限大まで広がっている．これは，コンパクト多様体の特異な極限として解釈でき，その場合，サイクルの一つが無限大の大きさに退化する．

ここでは，$A$サイクルを貫く$F_3$フラックスが$M$単位，$B$サイクルを貫く$H_3$フラックスが$-K$単位であると仮定する．すなわち， $$ \frac{1}{2\pi\alpha'}\int_A F_3 =2\pi M \quad \text{and} \quad \frac{1}{2\pi\alpha'}\int_B H_3 = -2\pi K $$ ポアンカレ双対性を用いると，スーパー・ポテンシャルは $$ W=\int G_3\wedge\Omega=(2\pi)^2\alpha'\left( M\int_B\Omega-K\tau\int_A \Omega \right) $$ コニフォールドの先端で縮退するサイクルを記述する複素座標は $$ z=\int_A \Omega $$ 前に議論した特殊幾何学によれば，$B$サイクルの周期を定義する座標（$A$サイクルの周期の関数）は，$A$サイクルの周期の関数である．より具体的には，コニフォールド特異点を記述しているので，前に導出した結果を用いると $$ \int_B \Omega=\frac{z}{2\pi i}\log z+\text{holomorphic} $$ これらの結果を用いると，スーパー・ポテンシャルのKähler共変微分は $$ \mathcal{D}_zW \simeq (2\pi)^2\alpha'\left( \frac{M}{2\pi i}\log z-i\frac{K}{g_s}+\cdots \right) $$ となる（$K/g_s$が大きい極限）[16]．このとき，$\mathcal{D}_zW=0$の解は $$ z \simeq e^{-2\pi K/Mg_s} $$ となる．例えば$M=1$，$K/g_s=5$とすると，大きな階層が得られる．この解ではディラトンは固定されていると仮定している．

ワープ因子の解は次のように見積もることができる．後で詳しく議論されるように，$N$個のD3-braneの近傍では，時空計量は $$ ds^2=\left( \frac{r}{R} \right)^2|d\vec{x}|^2 +\left( \frac{R}{r} \right)^2(dr^2+r^2d\Omega_5^2)\quad \text{with} \quad R^4=4\pi g_sN(\alpha')^2 $$ の形をとる．ここで $r$ はD3-braneからの距離であり，D3-braneは $r \simeq 0$ に位置している．D3-brane近傍でのワープ因子を見積もりたい．背景が変形コニフォールドであるため，$r$ の最小値は変形パラメータ $z$ によって $$ r_{\text{min}}\simeq\rho_{\text{min}}^{2/3}=z^{1/3}\simeq e^{-2\pi K/3Mg_s} $$ で決まる．これは，D3-brane近傍でワープ因子が小さく正の値に近づくことを示している．

モジュライ安定化

フラックスを伴うコンパクト化における重要な事実は，モジュライ場に対して非自明なスカラー・ポテンシャルが存在することである．これは驚くべきことではない，背景フラックスが幾何学を決定する方程式を修正するからである．モジュライ場の完全なスカラー・ポテンシャル $V$ は，前述したように標準的な超重力の公式からスーパー・ポテンシャルとKählerポテンシャルを用いて得られるか，あるいはここで行っているように直接の Kaluza–Klein 縮約によって得られる．

M理論のスカラー・ポテンシャル

以下では，Calabi-Yau four-fold上でのM理論のフラックスコンパクト化に対するスカラー・ポテンシャルを，式(10.3)の作用を式(10.5)で記述されるワープした幾何学上で低エネルギー展開することで導出する．これにより，式(10.62)から導かれる$W^{3,1}$に由来する制約が複素構造モジュライを安定化し，式(10.68)から導かれる$W^{1,1}$に由来する方程式がKählerモジュライを安定化することがさらに示される．

演習10.18で確認するように，フラックスはモジュライ場のスカラー・ポテンシャルを生成する． $$ V(T,K)=\frac{1}{4\mathcal{V}^3}\left( \int_M F\wedge\star F-\frac{1}{6}T_{M2}\chi \right) $$ ここで，節10.1と同様に$\kappa_{11}=1$と置く．ポテンシャルに寄与する項はフラックスの内部成分に由来する．$f_m$項は大きな体積極限で下位項を与えるため省略している．

$F$は4形式なので，Calabi-Yau four-foldの中間次元コホモロジーに属する．式(10.44)によれば，4形式の$(2,2)$成分はLefschetz分解を持つ： $$ F^{2,2}=F_o^{2,2}+J\wedge F_o^{1,1}+J\wedge JF_o^{0,0} $$ ここで添字$o$はフラックスがプリミティブであることを示す．式(10.67)で示したように，超対称解ではプリミティブ項，すなわち第1項のみが非ゼロである．しかしここでは超対称性破れの可能性を許すために全ての項を含める．第1項と第3項は自己双対，第2項は反自己双対であるため， $$ \star F^{2,2}=F^{2,2}-2J\wedge F_o^{1,1} $$ ここで$\star$は内部多様体上のHodge双対を表す．Exercise 10.4から $$ \star F^{4,0}=F^{4,0},\quad \star F^{3,1}=-F^{3,1} $$ が従い，$F$が実であることから$(0,4)$と$(1,3)$成分についても同様である．これらを合わせると，全体の4形式フラックスは次を満たす： $$ \star F=F-2F^{3,1}-2F^{1,3}-2J\wedge F_o^{1,1} $$ したがって$F$との外積をとるとき，式(10.168)に現れるフラックスの運動項は次の形に書き換えられる： $$ \int_MF\wedge\star F=\int_M F\wedge F-4\int_MF^{3,1}\wedge F^{1,3}-2\int_M J\wedge F_o^{1,1}\wedge J\wedge F_o^{1,1} $$ その他の項はHodge分解とLefschetz分解による直交性のため消える．これをスカラー・ポテンシャル式(10.168)に代入すると，式(10.173)右辺の第1項は，$N=0$のタッドポールキャンセル条件(10.60)により打ち消されることが分かる．結果としてスカラー・ポテンシャルに寄与するのは$F$の反自己双対成分のみである．

超対称性を破る解

上の解析から，運動方程式を満たす超対称性を破る解が存在することが導かれる．実際，次を満たす任意のフラックス $$ F=\star F,\quad F\notin H_{\text{primitive}}^{(2,2)} $$ は運動方程式の解となり，超対称性を破る． $$ F\sim \Omega, \quad F\sim J\wedge J $$ のようなフラックスがその例である．さらに，これらのフラックス成分はスカラー・ポテンシャルに現れないため，宇宙定数を生成しない．

スカラー・ポテンシャル

式(10.173)右辺の第2項は次のように書き換えられる． $$ \int_M F^{3,1}\wedge F^{1,3}=-e^{\mathcal{K}^{3,1}}G^{IJ}\mathcal{D}_{I}W^{3,1}\mathcal{D}_J\bar{W}^{3,1} $$ したがってこれは複素構造モジュライに対するスカラー・ポテンシャルを与える．この結果は $F^{3,1}$ を $(3,1)$ 型形式の基底に展開することで得られる．明示的な計算は演習10.5とかなり類似している．同様に，式(10.173)右辺の最後の項はKähler構造モジュライに対するポテンシャルを生成する． $$ \int_M J\wedge F_o^{1,1}\wedge J\wedge F_o^{1,1}=-\mathcal{V}^{-1}G^{AB}\mathcal{D}_AW^{1,1}\mathcal{D}_BW^{1,1} $$ ここで $$ \mathcal{D}_A=\partial_A-\frac{1}{2}\partial_{A}\mathcal{K}^{1,1},\quad \mathcal{K}^{1,1}=-3\log\mathcal{V} $$ かつ $G^{AB}$ は計量 $G_{AB}$ の逆行列である． $$ G_{AB}=-\frac{1}{2}\partial_A\partial_B\log\mathcal{V} $$ ここで $\mathcal{V}=\frac{1}{24}\int J^4$ は Calabi-Yau の体積である．以上より，スカラー・ポテンシャルは次の形をとる． $$ V(T,K)=e^{\mathcal{K}}G^{IJ}\mathcal{D}_IW^{3,1}\mathcal{D}_J\bar{W}^{3,1}+\frac{1}{2}\mathcal{V}^{-4}G^{AB}\mathcal{D}_AW^{1,1}\mathcal{D}_BW^{1,1} $$ ここで $\mathcal{K}=\mathcal{K}^{3,1}+\mathcal{K}^{1,1}$．このポテンシャルは明らかに非負であり，したがってこの方法では AdS$_3$ 空間へのコンパクト化は得られないことが示される．

radial modulus

式(10.180)のポテンシャルに全てのモジュライが寄与する必要はないことに注意せよ．例えば，コンパクト多様体$M$の全体体積を特徴づけるラジアルモジュラスはこのポテンシャルに依存しない．したがってこのモジュラスは安定化されない．その理由は，未破れ超対称性の条件式(10.65)，(10.66)，(10.67)や超対称性を破る解の存在条件式(10.174)が体積を定数倍する再スケーリングに対して不変であるためである．一見残念に思えるかもしれないが，これは好都合でもある．この自由度により，行った近似が正当化されるように体積を十分大きく選べる．体積が十分大きければ，M理論の高次導関数項の多くは無視できる．もちろん，非摂動的効果を含めると状況は変わる．そのような効果がラジアルモジュラスを安定化し，フラックス量子が大きい場合には行った計算が有効なままであると期待される．これは本節で議論したM理論のコンパクト化に特有の話ではなく，文献で議論される多くのフラックスコンパクト化にも当てはまる．非摂動的効果なしで全てのモジュライが安定化されるモデルは非常に少ない．

IIB型のスカラー・ポテンシャル