弦の幾何学
参考文献:K. Becker, M. Becker, J. Schwarz, "String Theory and M-Theory", Cambridge University Press, 2007.
超弦理論は10次元,M理論は11次元であるため,日常経験の4次元時空幾何学と接続するには何らかの工夫が必要となる.現在,主に2つのアプローチで研究されている[1].
Kaluza-Klein コンパクト化
より長い歴史を持つアプローチは,Kaluza-Kleinコンパクト化である.この方法では,余剰次元がサイズ $l_c$ のコンパクト多様体を形成する.このような次元は,エネルギー $E \ll 1/l_c$ で行われる観測では基本的に不可視である.しかし,そのトポロジーの詳細は,低エネルギーでの有効な4次元理論に現れるスペクトルや対称性に深い影響を与える.ここでは,これらの余剰次元の有望な幾何学について探究したい.主な焦点はCalabi-Yau多様体であるが,特殊ホロノミーを持つ他の多様体についても議論する.コンパクトなCalabi-Yau多様体は最も直接的な可能性であるが,非摂動的弦理論の最近の発展により,非コンパクトなCalabi-Yau多様体も重要であることが示されている.非コンパクトなCalabi-Yau多様体の例として,特にconifoldについて,説明したい.
brane-worldシナリオ
余剰次元を扱う第2の方法は,brane-worldシナリオである.このアプローチでは,日常経験する4次元は高次元時空に埋め込まれた「欠陥」として同定される.この欠陥は,通常,複数のbraneが一致または交差して形成される.この方法が有望である理由は,標準模型のようなYang-Millsゲージ場が開弦のゼロモードに対応し,それらはD-braneの世界体積上に存在する,という観察にある.
Kaluza-Kleinのアイデアの変種として,brane-worldシナリオでよく用いられるものがある.それは,余剰次元の幾何学が適切に「ワープ」していれば,余剰次元のサイズが従来の予想よりもはるかに大きくなり得る,という観察に基づいている.ワープしたコンパクト化では,4次元Minkowski時空の全体的なスケールが,コンパクト次元の座標に依存する.ここでは,より伝統的なKaluza-Kleinアプローチ,すなわち幾何学が内部多様体と外部多様体の直積である場合に焦点を当てる.ワープした幾何学とそれを用いたbrane-world構成については別で議論する.
動機
これまで余剰次元を記述する多様体として議論されてきたのは,円や円の積(トーラス)だけである.また,円の $\mathbb{Z}_2$ orbifold も何度か登場した.いずれかの10次元超弦理論を6次元トーラス上で4次元にコンパクト化した場合,得られる理論は現象論的には全く受け入れがたい.なぜなら,超対称性が全く破れないからである.つまり,どの10次元理論をコンパクト化するかによって,4次元では $\mathcal{N}=4$ または $\mathcal{N}=8$ 超対称性が残ることになる.ここでは,より現象論的に魅力的な可能性,すなわちorbifolds,Calabi-Yau多様体,特殊ホロノミー多様体などを探究する.これらの空間でのコンパクト化は,4次元でより少ない超対称性を持つ真空を導く.
現象論と接続するためには,4次元理論に次のような性質が求められる:
- 標準模型のゲージ群である $SU(3) \times SU(2) \times U(1)$ のYang-Millsゲージ群が現れること.
- 標準模型の超対称的な拡張として興味深いクラスの4次元理論は,高エネルギーで $\mathcal{N}=1$ 超対称性を持つ.この超対称性は,低エネルギーで観測される物理と接続するために,あるスケール(例えばTeV程度)で破れる必要がある.$\mathcal{N}=1$ 超対称性は,理論に計算上の制約を与えるが,$\mathcal{N}\geq2$ の場合のように理論を非現実的にするほど強い制約ではない. 10次元または11次元では,十分高いエネルギーでは超対称性が顕在化しているはずである.ここで検討されている問題は,コンパクト化のスケールと比べて低いエネルギー,すなわち有効な四次元理論が現れるエネルギー領域で,$\mathcal{N}=1$ 超対称性が存在するべきかどうかである.この点について興味深い証拠の一つは,超対称性が標準模型の三つのゲージ結合定数を約 $10^{16}$ GeV で統一させることであり,これはこのエネルギーで超対称的な大統一理論が実現されることを示唆している. 超対称性の技術的な利点は,双対性の議論やブラックホールの物理の文脈で利用されているように,弱結合から強結合への結果の転用が可能となり,強結合理論についての情報を得られる点にある.超対称的理論は,非超対称的な理論よりも解きやすい.超対称性による拘束条件は一次方程式を導き,運動方程式のような二次方程式よりも解きやすい.ここで考える背景のタイプでは,3形式場の強さに対するBianchi恒等式を満たす超対称性の拘束条件の解は,常に運動方程式の解となるが,逆は必ずしも成り立たない.
10次元ヘテロティック弦理論を内部多様体 $M$ 上でコンパクト化した場合,4次元で $\mathcal{N}=1$ 超対称性が得られる条件だが,ある仮定のもとで,内部多様体はCalabi-Yau three-foldでなければならないことが証明されている.
Calabi-Yau多様体
Calabi-Yau多様体は複素多様体であり,任意の偶数次元で存在する.より厳密には,Calabi-Yau $n$-foldとは,$n$次元の複素Kähler多様体で,$SU(n)$のホロノミーを持つものである.実2次元での例は,複素平面 $\mathbb{C}$ とトーラス $T^2$ だけである.トーラス以外のRiemann面はCalabi-Yauではない.4次元では,コンパクトな例としてK3多様体とトーラス $T^4$ があり,非コンパクトな例として $\mathbb{C}^2$ や $\mathbb{C} \times T^2$ などがある.最も重要なのはCalabi-Yau three-foldで,これは実6次元(または複素3次元)を持つ.低次元の場合と異なり,Calabi-Yau three-foldは何千種類も知られており,その数が有限かどうかも未解決である.Calabi-Yau three-foldへのコンパクト化は,元の超対称性の$3/4$を破る.したがって,ヘテロティック弦理論をCalabi-Yau three-foldでコンパクト化すると,4次元で $\mathcal{N}=1$ 超対称性が得られ,type II超弦理論の場合は $\mathcal{N}=2$ が得られる.
conifold転移と超対称サイクル
Calabi-Yauコンパクト化によって得られる4次元低エネルギー理論が一貫性を持つためには,結合定数に関する非摂動的効果を考慮する必要がある.例えば,超対称サイクルを巻くbraneから生じるmasslessの状態を,低エネルギー有効作用に含めなければならない.これらを考慮しない場合,計量が特異的になり,作用が矛盾することになる.
ミラー対称性
Calabi-Yau多様体へのコンパクト化には,T-双対性に関連した興味深い性質がある.これは,トーラスコンパクト化の特徴的な性質である.ここでは,特定のトーラスコンパクト化が,トーラスの形状とサイズの入れ替えに対して不変であるという,もう1つの顕著な性質を持つことを示す.これは,ミラー対称性と呼ばれる対称性の最も単純な例であり,より一般的なCalabi-Yau多様体にも現れる性質である.この性質は通常は異なるトポロジーを持つ2つの異なるCalabi-Yau多様体が物理的に等価となり得ることを意味する.より正確には,Calabi-Yau多様体$M$上でコンパクト化したtype IIA超弦理論は,ミラーCalabi-Yau多様体$W$上でコンパクト化したtype IIB超弦理論と等価である[2].ミラー対称性の証明に向けた進展についても議論したい.
特殊ホロノミー多様体
Calabi-Yau多様体は1985年以降盛んに議論されてきたが,近年では,弦理論の他の一貫した背景も研究されている.これは弦の双対性に動機づけられた部分もある.最も重要な例は,$G_2$および$Spin(7)$ホロノミーを持つ多様体である.$G_2$多様体は7次元であり,超対称性の$7/8$を破る.一方,$Spin(7)$多様体は8次元で,超対称性の$15/16$を破る.Calabi-Yau four-foldも8次元で,超対称性の$7/8$を破る.これらはフラックスコンパクト化の文脈で議論される.
目次
- Orbifolds
- Calabi-Yau多様体:定義と性質
- Calabi-Yau多様体の例
- ヘテロティック弦のCalabi-Yauコンパクト化
- Calabi-Yau three-fold上のtype IIA/IIB
- 補遺:幾何学とトポロジー
Orbifolds
Calabi-Yau多様体について議論する前に,より数学的に単純なコンパクト化空間のクラスであるorbifoldについて考える.内部空間の計量の明示的な形が分かっていると便利な場合があるが,ほとんどすべてのCalabi-Yau多様体についてはその計量は知られていない[3].これは4次元多様体K3についても同様である.orbifoldは,計量が明示的に分かっているCalabi-Yau多様体の特異な極限を含んでいる.
$X$ を滑らかな多様体,$G$ をその離散等長変換群とする.このとき,商空間 $X/G$ を構成できる.商空間の各点は,$X$ 上のある点と,その等長変換群によるすべての像からなる軌道に対応する.$G$ の非自明な元が $X$ の点を不変に保つ場合,商空間には特異点が生じる.一般相対論はこのような特異空間上では定義が困難である.しかし,弦理論では,いわゆる「twisted sectors」を考慮すれば,orbifold特異点を持つ空間上でも弦の伝播が一貫して定義できることが分かっている.非特異点では,orbifold $X/G$ は局所的には元の多様体 $X$ と区別がつかない.したがって,計量などの局所的な構造は,orbifoldの非特異領域に自然に誘導できる.ここでは,orbifold群の作用は空間次元のみに及ぶと仮定する.時間方向に作用させると,閉じた時間的曲線など新たな現象が現れる可能性がある.
いくつかの単純な例
コンパクトな例:円は実直線上の点を $x \sim x+2\pi R$ のように同一視することで得られる.最も単純なorbifoldの例は,円周座標 $x$ に対して $x \to -x$ という同一視を行った後に得られる区間 $S^1/\mathbb{Z}_2$ である.この同一視により,円は図に示すように区間へと変換される.このorbifoldは,$E_8 \times E_8$ ヘテロティック弦の強結合極限と関連して重要な役割を果たす.
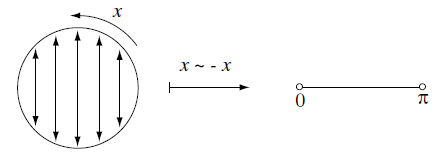
非コンパクトな例:非コンパクトなorbifoldの単純な例として,複素平面 $\mathbb{C}$ を考え,通常通り局所座標 $z$ で記述する.ここで,等長変換として $$ z \to -z $$ という操作を考える.この操作は2回適用すると元に戻るため,2元群 $\mathbb{Z}_2$ を生成する.orbifold $\mathbb{C}/\mathbb{Z}_2$ は,群作用による同じ軌道上の点,すなわち $z$ と $-z$ を同一視することで定義される.大まかに言えば,この操作は複素平面を2つの半平面に分割することに対応する.より正確には,このorbifoldは上半平面を取り,境界(実軸)の左半分と右半分を群作用に従って同一視することに対応する.図に示すように,この結果得られる空間は円錐となる.
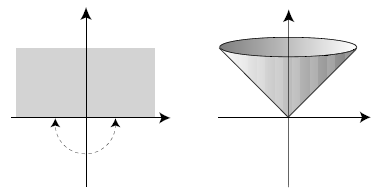
このorbifoldは,群作用の不動点である原点$(0, 0)$に円錐特異点を持つことを除けば滑らかである.円錐特異点の帰結の一つは,原点を中心とする半径 $R$ の円周の長さが $\pi R$ となり,円錐の欠損角も $\pi$ となることである.明らかな一般化として,群が $2\pi/N$ の回転で生成される $\mathbb{C}/\mathbb{Z}_N$ というorbifoldがある.この場合も原点に特異点があり,円錐の欠損角は $2\pi(N-1)/N$ となる.この種の特異点は $A_N$ 特異点と呼ばれる.これは,より一般的なADE分類に含まれ,その詳細は後に議論される.
この例は,次の一般的な事実を示している:ある非自明な群元で不変(固定)となる点は,商空間の特異点に写る.特異点が存在するため,これらの商空間は(定義により滑らかである)多様体ではなく,代わりに「orbifold」と呼ばれる.すべての離散群作用が固定点を持つとは限らない.例えば,$z \to z + a$ という並進で生成される群による商空間 $\mathbb{C}/\mathbb{Z}$ は円筒となる.固定点が存在しないため,円筒は滑らかな多様体であり,orbifoldとは呼ばれない.2つの周期があり,その比が実数でない場合,商空間 $\mathbb{C}/(\mathbb{Z} \times \mathbb{Z})$ は滑らかなトーラスとなる.
状態のスペクトル
orbifold背景に存在する自由弦のスペクトルには,どのような物理的状態が現れるだろうか?一般に,2種類の状態が存在する.
- 最も明白なクラスの状態は「untwisted state」と呼ばれ,これは $X$ 上に存在し,群 $G$ に対して不変な状態である.すなわち,$X$ 上の弦状態のHilbert空間を $G$ 不変な部分空間に射影することができる.$X$ 上の弦状態 $\Psi$ がorbifold $X/G$ 上の弦状態に対応するためには, $$ g\Psi=\Psi \quad\text{for all}\quad g\in G $$ を満たす必要がある.有限群 $G$ の場合,任意の $X$ 上の状態 $\Psi_0$ から,そのすべての像 $g\Psi_0$ を重ね合わせることで $G$ 不変な状態 $\Psi$ を構成できる.
- orbifold上の物理的弦状態にはもう一つのクラスがあり,これは弦が拡がった(extended)対象であることに由来する.これらの状態は「twisted state」と呼ばれ,次のようにして得られる.ここでは閉弦理論を仮定しているので,弦は同じ点から始まり同じ点で終わらなければならない,すなわち $X^{\mu}(\sigma+2\pi)=X^{\mu}(\sigma)$ である.$X$ 上のある点とその $G$ による像を結ぶ弦は $X$ 上では許されないが,$X/G$ 上では許される閉弦配置に写る.数学的には, $$ X^{\mu}(\sigma+2\pi)=gX^{\mu}(\sigma) $$ を満たす $g\in G$ が存在する.untwisted stateでは $g=1$ に対応する.twisted stateは,orbifold化によって新たに現れる閉弦状態である.一般に,twisted sectorは $G$ の共役類によってラベル付けされる.$G$ が非可換群の場合のみ,この区別が重要となる. 例えば $\mathbb{C}/\mathbb{Z}_2$ の場合,twisted stateはorbifoldの特異点を囲むことが明らかである.これはorbifoldに共通する特徴である.量子スペクトルでは,twisted sectorの個々の量子状態は,古典的配置が囲むorbifold特異点に局在する.少なくとも低い励起については,弦が小さなサイズに縮むため,このことが明確である.
orbifoldと超対称性の破れ
一般に,orbifold $X/G$ 上の弦理論は,元の空間 $X$ 上よりも超対称性が少なくなるため,現象論的により魅力的となる.この仕組みがどのように働くかを,上で述べた例を一般化した,非コンパクトなorbifold,すなわち $$ \mathbb{C}^n/\mathbb{Z}_N $$ 型のorbifoldについて考察する.ここで得られる超対称性の破れに関する結論は,コンパクトな $$ T^{2n}/\mathbb{Z}_N $$ 型のorbifoldにも適用できる.
$\mathbb{C}^n$ を座標 $(z_1, \ldots, z_n)$ でパラメータ化し,$\mathbb{Z}_N$ の生成元 $g$ を各平面の同時回転として定義する: $$ g: z^a \to e^{i\phi^a}z^a,\quad a=1,\ldots,n $$ ここで $\phi^a$ は $2\pi/N$ の整数倍であり,$g^N=1$ となる.円錐の例は $n=1, N=2, \phi^1=\pi$ に対応する.
破れない超対称性は,元の超電荷 $Q_{\alpha}$ のうち群作用で不変な成分である.この例では群作用が回転なので,超電荷がスピノルであることを考慮し,スピノルがこの回転でどのように変換されるかを調べる必要がある.$2n$ 次元における回転生成子のスピノル表現のウェイトは $(\pm\frac{1}{2}, \pm\frac{1}{2}, \ldots, \pm\frac{1}{2})$ の形をしており,全部で $2^n$ 個の状態がある.これは上式の指数を2で割ることに対応し,スピノルが $2\pi$ 回転で符号が反転するというよく知られた事実を説明する.$Spin(2n)$ の既約スピノル表現の次元は $2^{n-1}$ である.負のウェイトの個数が偶数のものが一方のスピノル表現,奇数のものがもう一方のスピノル表現となる.上記と同じ回転の下で $$ g:Q_\alpha \to \exp\left( i\sum_{a=1}^{n}\varepsilon_\alpha^a\phi^a \right)Q_\alpha $$ となる.ただし $\varepsilon$ はスピノルのウェイトである.例えば $\phi_a$ が $$ \frac{1}{2\pi}\sum_{a=1}^{n}\phi^a=0\quad\text{mod $N$} $$ を満たすとする.このとき一般には,$g$ の下で不変となる $Q_\alpha$ の成分は,すべての $n$ 成分についてウェイトが同じ符号を持つものだけである.すなわち $\sum_a \varepsilon_\alpha^a \phi^a = 0$ となる場合である.特別な場合には他の成分も不変となることがある.不変でないウェイトごとに,破れない超対称性の量は半分に減る.したがって,たった1つのウェイトだけが不変な場合,破れない超対称性の割合は $2^{1-n}$ となる.ここでは,Calabi-Yau $n$-fold へのコンパクト化でも同じ割合の超対称性が保存されることを示す.実際,この型のいくつかの orbifold は,滑らかな Calabi-Yau 多様体の特異極限となっている.
Calabi-Yau多様体:定義と性質
定義によれば,Calabi-Yau $n$-fold とは,$n$ 次元の複素Kähler多様体であり,第1Chern類が消えているものを指す: $$ c_1 = \frac{1}{2\pi}[\mathcal{R}] = 0 $$ Calabiによって予想されYauによって証明された定理によれば,$c_1=0$ を持つ任意のコンパクトKähler多様体は,$SU(n)$ ホロノミーを持つKähler計量を持つ.この後述べるように,$SU(n)$ ホロノミーを持つ多様体は,共変的に定数なスピノル場を持ち,その結果として必ずRicci平坦となる.この定理はコンパクト多様体の場合にのみ成り立つ.非コンパクトの場合には,無限遠で追加の境界条件を課す必要がある.そのため,$SU(n)$ ホロノミーを持つ計量は,ちょうど第1Chern類が消えるKähler多様体に対応する.
上記の定理を動機づけるために,共変的に定数なスピノルが存在すると背景がKählerかつ$c_1=0$となることを示す.基本定理として,コンパクトなKähler多様体は,$c_1=0$ であることと,消えない正則な$n$-形式を持つことが同値である.局所座標で書くと, $$ \Omega(z^1,z^2,\ldots,z^n)=f(z^1,z^2,\ldots,z^n)dz^1\wedge dz^2\wedge\cdots\wedge dz^n $$ となる.後で,$SU(n)$ホロノミーを持つ背景でこのような$\Omega$を明示的に構成することで,$c_1$が消えることを示す.
Calabi-Yau $n$-foldのHodge数
Betti数は多様体に付随する基本的な位相不変量である.Betti数 $b_p$ は多様体 $M$ の $p$ 次de Rhamコホモロジー $H^p(M)$ の次元であり,その定義は補遺で述べる.多様体に計量が与えられている場合,Betti数は多様体上の線形独立な調和$p$-形式の個数を数える.Kähler多様体の場合,Betti数はHodge数 $h^{p,q}$ に分解でき,これは多様体上の調和$(p,q)$-形式の個数を数える: $$ b_k = \sum_{p=0}^{k} h^{p, k-p} $$
Hodgeダイヤモンド
Calabi-Yau $n$-fold は,その Hodge 数の値によって特徴づけられる.ただし,これは完全な特徴づけではなく,異なる Calabi-Yau 多様体が同じ Hodge 数を持つ場合もある.Hodge 数の間には対称性や双対性があり,独立なものはごく一部である.Calabi-Yau $n$-fold の Hodge 数は次の関係式を満たす: $$ h^{p,0}=h^{n-p,0} $$ これは,空間 $H^p(M)$ と $H^{n-p}(M)$ が同型であることから導かれる.これは,閉じた $(p,0)$-形式と,正則な $(n,0)$-形式の複素共役を計量で縮約し,閉じた $(0, n-p)$-形式を作ることで証明できる.複素共役により次の関係も成り立つ: $$ h^{p,q}=h^{n-q,n-p} $$ 任意のコンパクト連結Kähler複素多様体では $h^{0,0}=1$ であり,これは定数関数に対応する.単連結多様体では基本群(第1ホモトピー群)が消え,したがって第1ホモロジー群も消える.その結果[5], $$ h^{1,0}=h^{0,1}=0 $$
重要な場合として $n=3$ のとき,Calabi-Yau 多様体のコホモロジー的な特徴づけは $h^{1,1}$ と $h^{2,1}$ を指定するだけで十分である.全ての Hodge 数は Hodge ダイヤモンドで表すことができる.
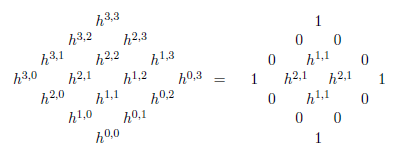
上述の関係式を用いると,Calabi-Yau 3-fold の Euler標数は次のように与えられる: $$ \chi=\sum_{p=0}^{6}(-1)^p b_p=2(h^{1,1}-h^{2,1}) $$
後で,M理論のCalabi-Yau four-foldへのコンパクト化について議論する.これは $n=4$ の場合に対応する.これらの多様体は,3つの独立なHodge数 $h^{1,1}$,$h^{1,3}$,$h^{1,2}$ によって特徴づけられる.Hodgeダイヤモンドは次のような形をしている.
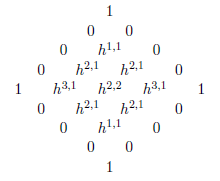
Calabi-Yau four-foldでは,Hodge数の間に追加の関係式が存在する(ここでは導出しない): $$ h^{2,2}=2(22+2h^{1,1}+2h^{1,3}-h^{1,2}) $$ その結果,Hodge数のうち独立に変化させられるのは3つだけである. Euler標数は次のように書ける: $$ \chi=\sum_{p=0}^{8}(-1)^pb_p=6(8+h^{1,1}+h^{3,1}-h^{2,1}) $$
Calabi-Yau多様体の例
Calabi-Yau one-fold
最も単純なCalabi-Yau多様体の例は,1つの複素次元を持つものである.
非コンパクトな例($\mathbb{C}$):非コンパクトな最も単純な例は複素平面である.複素座標 $(z, \bar{z})$ で記述され,平坦な計量 $$ ds^2=|dz|^2 $$ を持つ.このとき,正則な1-形式は $$ \Omega=dz $$ である.
コンパクトな例($T^2$):唯一のコンパクトなCalabi-Yau one-foldは2次元トーラス $T^2$ である.これは平坦な計量を持ち,向かい合う辺を同一視した平行四辺形として考えることができる.この単純な例は,ミラー対称性など高次元にも一般化できる概念を導入するために,後で議論されている.
Calabi-Yau two-fold
非コンパクトな例:非コンパクトなCalabi-Yau two-fold(複素2次元Calabi-Yau多様体)の簡単な例は,前節で挙げた多様体の直積として構成できる: $$ \mathbb{C}^2 = \mathbb{C} \times \mathbb{C}, \quad \mathbb{C} \times T^2 $$
コンパクトな例($T^4$, K3):共変的に定数なスピノルが存在するという条件は,実4次元では非常に制限的である.実際,K3と$T^4$だけが,4次元のコンパクトKähler多様体でこの条件を満たす例である.その結果,これらの多様体のみがCalabi-Yau two-fold(複素2次元Calabi-Yau多様体)の例となる.ホロノミーが$SU(2)$(その部分群ではなく)であることを要求すると,K3だけが残る.対照的に,Calabi-Yau three-fold(複素3次元Calabi-Yau多様体)は非常に多く(おそらく無限に)存在する.K3と$T^4$はいずれもCalabi-Yau多様体なので,Ricci平坦なKähler計量を持つ.さらに,$SU(2) = Sp(1)$ であることから,これらはハイパーKähler多様体でもある[6].滑らかなK3のRicci平坦計量の明示的な形は知られていないが,K3はorbifold極限でより詳細に記述できる.次にその説明を行う.
K3多様体の特異極限として,しばしば弦理論で用いられるのが $T^4$ の orbifold である.この構成は計量などを完全に明示的に書けるという利点がある.具体的には,正方形型の $T^4$ を $$ z^a \sim z^a + 1,\quad z^a \sim z^a + i,\quad a=1,2 $$ という4つの離散的な同一視を課すことで構成する.この空間には $$ \mathcal{I}:(z^1, z^2) \to (-z^1, -z^2) $$ という $\mathbb{Z}_2$ 等長変換群が作用している.この $\mathbb{Z}_2$ の作用には16個の不動点があり,それぞれの $z^a$ が $$ 0,\quad \frac{1}{2},\quad \frac{i}{2},\quad \frac{1+i}{2} $$ のいずれかの値を取る場合に対応する.したがって,orbifold $T^4/\mathbb{Z}_2$ には16個の特異点が存在する.これらの特異点は,orbifold の特異点を「解消」する「blow-up」という数学的操作によって滑らかにすることができる.
上述の orbifold の特異点は,Eguchi-Hanson 空間を挿入することで「解消」することができる.具体的には,各不動点のまわりに半径 $a$ の小さな球を切り取る.その球の境界は $S^3/\mathbb{Z}_2$ となる(球面上の対蹠点を同一視するため).各球を切り取り,その代わりに境界が $S^3/\mathbb{Z}_2$ であり,かつ滑らかで非コンパクトなRicci平坦Kähler多様体を挿入する.16個の切り取った球それぞれに挿入できる,これらの条件を満たす唯一の多様体が Eguchi-Hanson 空間である.Eguchi-Hanson 空間の計量は次のように与えられる: $$ ds^2 = \Delta^{-1} dr^2 + \frac{1}{4} r^2 \Delta (d\psi + \cos\theta\, d\phi)^2 + \frac{1}{4} r^2 d\Omega_2^2 $$ ここで $\Delta = 1 - (a/r)^4$,$d\Omega_2^2 = d\theta^2 + \sin^2\theta\, d\phi^2$ である.動径座標 $r$ の範囲は $a \leq r < \infty$ であり,$\psi$ の周期は $2\pi$ である.
このように特異点を修復することで,所望のトポロジーを持つ多様体が得られるが,真のCalabi-Yau幾何学とするためには計量を滑らかにする必要がある.orbifoldは $a \to 0$ の極限に対応する.Eguchi-Hanson空間の非自明なHodge数は $h^{0,0}=h^{1,1}=h^{2,2}=1$ である. さらに,(1,1)-形式は反自己双対であり,次式で与えられる: $$ J=\frac{1}{2}rdr\wedge(d\psi+\cos\theta\, d\phi)-\frac{1}{4}r^2\sin\theta\, d\theta\wedge d\phi $$ 複素座標 $$ z_1=r\cos(\theta/2)\exp\left[ \frac{i}{2}(\psi+\phi) \right],\quad z_2=r\sin(\theta/2)\exp\left[ \frac{i}{2}(\psi-\phi) \right] $$ を用いると,この計量はKählerであり,Kählerポテンシャルは $$ \mathcal{K}=\log\left[ \frac{r^2\exp\left((r^4+a^4)^{1/2}\right)}{a^2+(r^4+a^4)^{1/2}} \right] $$ で与えられる.
K3のコホモロジーは,$T^4$とEguchi-Hanson空間の寄与を組み合わせることで計算できる.この方法で得られる結果は,計量を滑らかにした後も正しいままである.
Eguchi-Hanson空間は,それぞれの特異点を解消するために用いられる16個の空間ごとに,$H^{1,1}$の生成元を1つずつ,合計16個寄与する.さらに,$T^4$上では,次の4つの$H^{1,1}$コホモロジー類の代表が$\mathbb{Z}_2$同一視の下で残る: $$ dz^1\wedge d\bar{z}^1,\quad dz^2\wedge d\bar{z}^2,\quad dz^1\wedge d\bar{z}^2,\quad dz^2\wedge d\bar{z}^1 $$ これにより,$h^{1,1}=20$となる.加えて,$dz^1\wedge dz^2$で表される$H^{2,0}$クラスが1つ,$d\bar{z}^1\wedge d\bar{z}^2$で表される$H^{0,2}$クラスが1つ存在する.結果として,K3のHodge数はHodgeダイヤモンドで与えられる.
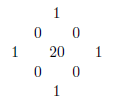
したがって,K3の非自明なBetti数は $b_0 = b_4 = 1,\, b_2 = 22$ であり,Euler標数は $\chi = 24$ となる.22個の非自明な調和2-形式は,3つの自己双対形式($b_2^+ = 3$)と19個の反自己双対形式($b_2^- = 19$)から構成される.
Calabi-Yau $n$-fold
Calabi-Yau $n$-fold($n>2$)の完全な分類は未解決の問題であり,特にコンパクトなCalabi-Yau three-foldの個数が有限かどうかすら分かっていない.多くの例が構成されているが,ここではそのいくつかを紹介する.
Calabi-Yau $n$-fold の例は,$n > 1$ のすべての場合において,射影空間 $\mathbb{C}P}^{n+1}$ の部分多様体として構成することができる.複素射影空間 $\mathbb{C}\mathbb{P}^n$(単に $\mathbb{P}^n$ とも書かれる)は,$n$ 複素次元のコンパクト多様体である.これは,$n+1$ 次元複素ベクトル空間 $\mathbb{C}^{n+1}/\{0\}$ から,すべての成分がゼロでない点の集合(すなわち $(z^1, z^2, \ldots, z^{n+1})$ で $z^i$ がすべてゼロでないもの)を取り,次の同一視を課すことで構成される: $$ (z^1, z^2, \ldots, z^{n+1}) \sim (\lambda z^1, \lambda z^2, \ldots, \lambda z^{n+1}) $$ ここで $\lambda$ はゼロでない任意の複素数である.したがって,$\mathbb{C}^{n+1}$ の直線が $\mathbb{C}P^n$ の点に対応する.
$\mathbb{C}P^n$(複素射影空間)はKähler多様体だが,Calabi-Yau多様体ではない.最も単純な例は $\mathbb{C}P^1$ であり,これは位相的には2次元球面 $S^2$ に対応する.明らかに,これはRicci平坦な計量を持たない.$\mathbb{C}P^n$ の標準的な計量は「Fubini-Study計量」と呼ばれ,次のように構成される.まず,多様体を $z^a \neq 0$ で定義される $n+1$ 個の開集合で被覆する.それぞれの開集合上で局所座標を導入する.例えば $z^{n+1} \neq 0$ の開集合では,$w^a = z^a / z^{n+1}$($a=1,\ldots,n$)と定義する.この開集合上でのKählerポテンシャルは $$ K = \log\left( 1 + \sum_{a=1}^{n} |w^a|^2 \right) $$ で与えられる.このKählerポテンシャルから,付録で与えられる公式に従って計量が決まる.重要な要件として,他の開集合でのKählerポテンシャルも同様の形で定義されるが,これらはKähler変換によって互いに異なることが必要である.
Calabi-Yau多様体の例は,複素射影空間の部分多様体として構成できる.具体的には,$z^a$ を $\mathbb{C}^{n+2}$ の座標とし,次数 $k$ の斉次多項式 $G$ を考えると, $$ G(\lambda z^1,\ldots,\lambda z^{n+2})=\lambda^k G(z^1,\ldots,z^{n+2}) $$ となる.$G(z^1,\ldots,z^{n+2})=0$ で定義される部分多様体は,$n$ 複素次元のコンパクトKähler多様体となる.この部分多様体の第1Chern類は $k=n+2$ のとき消える.これを示す一つの方法は,$X$ がKähler多様体であることから体積形式を用いて $c_1(X)$ を明示的に計算することである.体積形式としては,$\mathbb{C}P^{n+1}$ のKähler形式の$(n-1)$乗の引き戻しを用いることができる.もう一つの方法は,代数幾何学の随伴公式を用いることであり,これによれば $$ c_1(X) \sim [k-(n+2)]c_1(\mathbb{C}P^{n+1}) $$ となり,$k = n + 2$ のとき消える.
- $n=2$($\mathbb{C}P^3$ 内の4次多項式)の場合,K3多様体が得られる.例えば, $$ \sum_{a=1}^{4}(z^a)^4=0 $$ という4次方程式はK3を表す.4次多項式の選び方を変えることで,異なる複素構造を持つが微分同相なK3多様体が得られる.Calabi-Yau多様体の変形,特に複素構造の変形については後述する.
- $n=3$ の場合,この構成は $\mathbb{C}P^4$ 内の5次超曲面(quintic)を与える.この多様体は $$ \sum_{a=1}^{5}(z^a)^5=0 $$ または5変数のより一般的な5次多項式で表される.この多様体のHodge数は $$ h^{1,1}=1,\quad h^{2,1}=101 $$ であり,Euler標数は $\chi = -200$ となる.quintic多項式の係数を変えることは,やはり複素構造の変形に対応する. この多様体は,$z^a \neq 0$($a=1,\ldots,5$)で定義される5つの開集合で被覆できる.例えば,最初の開集合上では,局所座標 $w^a = z^a/z^1$($a=2,3,4,5$)を導入できる.これらは $$ \sum_{a=2}^5(w^a)^4dw^a=0 $$ を満たす.この座標で,正則な3-形式は $$ \Omega=\frac{dw^2\wedge dw^3 \wedge dw^4}{(w^5)^4} $$ で与えられる.上式は一つの座標を特別扱いしているように見えるが,一つ前の式を考慮すると,4つの座標 $w^a$($a=2,\ldots,5$)は対等に扱われていることが分かる.
一般化の一つは,射影空間 $\mathbb{C}P^n$ を加重複素射影空間 $W\mathbb{C}P^n_{k_1\cdots k_{n+1}}$ に置き換えることである.この$n$次元複素空間は,$\mathbb{C}^{n+1}$ から始めて,次の同一視を課すことで定義される: $$ (\lambda^{k_1}z^1,\lambda^{k_2}z^2,\ldots,\lambda^{k_{n+1}}z^{n+1})\sim (z^1,z^2,\ldots,z^{n+1}) $$ ここで $k_1,\ldots,k_{n+1}$ は正の整数であり,$\lambda$ は任意の非零複素数である.$N$ はこれらの最小公倍数である. さらに一般化として,次元 $n_i$ のこのような空間の直積を考えることもできる.座標のスケーリング性を保つような $m$ 個の多項式制約方程式を課すことができる.一般には,これにより$\sum n_i - m$複素次元の空間が得られる.その後,第1Chern類を計算する必要があるが,これは一般には容易ではない.それでもこの手法は自動化されており,数千種類の非同値なCalabi-Yau three-foldが得られている.さらに,トーリック幾何学(ここでは扱わない)に基づく強力な手法によっても多くの例が構成されている.これだけの努力にもかかわらず,Calabi-Yau three-foldの分類はまだ完成していない.
ヘテロティック弦のCalabi-Yauコンパクト化
10次元ヘテロティック弦理論のCalabi-Yauコンパクト化は,4次元時空において$\mathcal{N}=1$超対称性を持つ理論を与える.言い換えれば,元々の16個の超対称性のうち3/4が破れることになる.序論で述べたように,この動機は,現実の世界でもこの程度の超対称性がTeVスケールまで拡張されているという魅力的だが未証明の可能性にある.これらのコンパクト化を考えるもう一つの動機は,標準模型のゲージ群や大統一ゲージ群を,$E_8 \times E_8$ヘテロティック弦理論の2つの$E_8$群のうちの1つに比較的容易に埋め込むことができる点である.
10次元時空幾何のためのansatz
10次元時空$M_{10}$が非コンパクトな4次元時空$M_4$と小さくコンパクトな6次元内部多様体$M$の直積として分解されると仮定する. $$ M_{10}=M_4 \times M $$ これまで,10次元座標はギリシャ文字添字で表記し$ x^{\mu} $とした.ここでは,$ x^{M} $が$M_{10}$の座標を,$ x^{\mu} $が$M_4$の座標を,$ y^{m} $が6次元空間$M$の座標をそれぞれ表すという記法を用いる.この添字規則は$M=(\mu; m)$と要約される.式(9.41)の仮定の一般化はChapter 10で論じる.
最大対称解
$M_4$が最大対称,すなわち同次で等方的な4次元時空である解を考える.対称性だけから$M_4$のRiemannテンソルはその計量を用いて次のように表される: $$ R_{\mu\nu\rho\lambda}=\frac{R}{12}(g_{\mu\rho}g_{\nu\lambda}-g_{\mu\lambda}g_{\nu\rho}) $$ ここでスカラー曲率 $R = g^{\mu\nu}R_{\mu\nu}$ は定数である.これは4次元の宇宙定数に比例する.最大対称性は時空$M_4$をMinkowski($R=0$),AdS($R< 0$),またはdS($R>0$)のいずれかに制限する.$M_4$に沿った最大対称性の仮定は,NS-NS三形式場強度$H$およびYang-Mills場強度の以下の成分が消えることも要求する: $$ H_{\mu\nu\rho}=H_{\mu\nu\rho}=H_{\mu np}=0,\quad F_{\mu\nu}=F_{\mu n}=0 $$ 本章ではさらに,内部の三形式場強度 $H_{mnp}$ を零とし,ディラトン$\Phi$を定数と仮定する.これらの仮定は簡略化のためのものであり,これにより本章で記述する背景が得られる.内部で非零のH場や非定数のディラトンを持つ背景はChapter 10で議論する.
超対称性の破れない条件
保存された $N=1$ 超対称性が真空に課す拘束は次のように現れる.各超対称生成子 $Q$ は全ての場に対する無限小変換を生成し,それに対応する無限小パラメータを $\varepsilon$ とする.不変な超対称性は特定の背景を不変に保つ.これは真空状態が生成子によって消されるという量子的主張の古典版である.ボソン場の不変性は自明である,なぜならボソン場の超対称変分の各項は少なくとも一つのフェルミオン場を含み,古典背景ではフェルミオン場は消えるからである.したがって,非自明な条件はフェルミオンの変分からのみ生じる. $$ \delta_{\varepsilon}(\text{fermionic fields})=0 $$ 実際この理由のために,Chapter 8 ではフェルミオンの超対称変換のボソニック成分のみが示された.フェルミオンの期待値が超対称変分を行った後も依然として零であるならば,そのとき得られる解はここで考えている型の背景に対して超対称性を保存するボソニック運動方程式の解となる.実際,Exercise 9.4 が示すように,超対称性拘束の解は常に運動方程式の解であるが,その逆は必ずしも成り立たない.ここでは局所超対称性を持つ理論に対してこの結果を適用している.これは三形式 $H$ が満たす Bianchi 恒等式を追加の拘束として課せば可能である.不変な $N=1$ 超対称性を得るためには,Eq. (9.44) が4つの線形独立な選択の $\varepsilon$ について成り立ち,これらが4成分の Majorana スピノル(あるいは同等に2成分の Weyl スピノルとその複素共役)を構成する必要がある.
ヘテロティック弦理論の超重力近似はSection 8.1で記述されている.特に,10次元作用のボソン部が示されている.完全な超重力近似にはフェルミオン場に関わる項も含まれ,理論が$N=1$の局所超対称性(フェルミオンに対する16の対称性)を持つように組み込まれている.Section 8.1で述べたように,フェルミオン場の超対称変換のボソン項は次の形に書ける. \begin{align*} \delta\Psi_{M} =& \nabla_M\varspilon-\frac{1}{4}\bm{H}_M\varepsilon \\ \delta\lambda =& -\frac{1}{2} \slashed{\partial} \Phi\varepsilon+\frac{1}{4}\varepsilon \\ \delta\chi =& -\frac{1}{2}\bm{F}\varepsilon \end{align*} 文字列フレームにおける.さらに,三形式場強度 $H$ は次を満たす. $$ dH=\frac{\alpha'}{4}[\mathrm{tr}(R\wedge R)-\mathrm{tr}(F\wedge F)] $$ 左辺は完全形式である.したがって,$\mathrm{tr}(R\wedge R)$ と $\mathrm{tr}(F\wedge F)$ のコホモロジー類は一致していなければならない.ブレーンを含むコンパクト化では,この条件は追加寄与によって修正され得る.
フラックス $H$ が零と仮定すると,グラビティーノの超対称変換は簡約化され, $$ \delta\Psi_M=\nabla_M\varepsilon $$ 未破れの超対称性ではこれが零でなければならず,したがって Killing spinor 方程式の非自明な解が存在する必要がある, $$ \nabla_M\varepsilon=0 $$ この方程式は,$\varepsilon$ が共変的に定数なスピノルであることを意味する.
$N=1$ 超対称性は,そのようなスピノルが1つ存在することを意味する.内部多様体 $M_{10}$ が直積であるため,共変的に定数なスピノルは次のような直積構造に分解できる $$ \varepilon(x,y)=\zeta(x)\otimes\eta(y) $$ またはそのような項の和として表されることがある.反交換(Grassmann-odd)スピノルをこのように分解する場合,時空側の成分 $\zeta(x)$ は反交換(Grassmann-odd),内部側の成分 $\eta(y)$ は可換(Grassmann-even)であると常に理解される.
外部空間の性質
式 (9.48) の外部成分で,添字が値 $M=\mu$ を取る場合を考える.$M_4$ 上に共変的に定数なスピノル $\zeta(x)$ が存在し,次を満たすと仮定する: $$ \nabla_{\mu}\zeta=0 $$ すると式 (9.42) に現れる曲率スカラー $R$ は消え,ゆえに $M_4$ は Minkowski 時空となる.これは $$ [\nabla_{\mu},\nabla_{\nu}]\zeta=\frac{1}{4}R_{\mu\nu\rho\sigma}\Gamma^{\rho\sigma}\zeta=0 $$ と最大対称性の仮定 (9.42) から従う.詳細は Exercises 9.6 および 9.7 に示されている. このとき $\zeta$ は共変的に定数であるだけでなく実際に定数となり,4次元における未破れの大域的超対称性の無限小変換パラメータとなる.これは自明でない結果である.というのは,未破れの超対称性だけでは必ずしも宇宙定数が零になることを意味しないからである.AdS 空間も超対称的になり得る点は Chapter 12 で重要な役割を果たす.しかしながらこの結果は宇宙定数問題を解くものではない.現実と接続するために答えるべき問いは,超対称性が破れる場合に宇宙定数が零になり得るか,あるいは少なくとも極めて小さくなり得るかどうかである.本結果は未破れの超対称性を要求して導かれているため,この点については何も述べていない. 要約すると,超対称性は外部空間を4次元の Minkowski 時空に制約する.
内部多様体の性質
式 (9.48) の内部成分 $M=m$ から生じる拘束を考える.内部上で共変的に定数なスピノル $$ \nabla_{m}\eta=0 $$ が存在することは,可積分性条件 $$ [\nabla_m,\nabla_n]\eta=\frac{1}{4}R_{mnpq}\Gamma^{pq}\eta=0 $$ を導く.これにより内部多様体 $M$ の計量が Ricci 平坦であることが従い(Exercises 9.6 および 9.7 を参照), $$ R_{mn}=0 $$ が成り立つ.しかし,最大対称性を仮定した外部時空とは対照的に,これは $M$ が平坦であることを意味しない.なぜなら Riemann テンソルは依然として非零であり得るからである.
ホロノミーと破れない超対称性
向き付け可能な6次元スピン多様体,ここで主に関心のあるケースでは,スピノルを閉曲線に沿って平行移動すると,一般に $Spin(6)=SU(4)$ の行列による回転が生じる.これが一般的なホロノミー群である.このような多様体上の実スピノルは8成分を持つが,その8成分は2つの既約 $SU(4)$ 表現に分解できる. $$ \bm{8}=\bm{4}\oplus\bar{\bm{4}} $$ ここで $\bm{4}$ と $\bar{\bm{4}}$ は互いに複素共役であり,反対のチャイラリティを持つスピノルを表す.したがって,定まったチャイラリティを持つスピノルは $4$ 個の複素成分を持つ.
共変的に定数なスピノルは,閉曲線に沿って平行移動されても変化しない.このようなスピノルの存在は,何らかの超対称性が破れずに残るために必要である.式(9.48)を参照.$SU(4)$ のうち,定まったチャイラリティを持つスピノルが不変となり得る最大の部分群は $SU(3)$ である.理由は,$\bm{4}$ が $SU(3)$ に対して次の分解を持ち, $$ \bm{4}=\bm{3}\oplus\bm{1} $$ であり,そのシングレット(単位表現)は $SU(3)$ 変換に対して不変であるからである.四次元での未破れの超対称性 $N=1$ が存在する条件は,内部の六次元多様体上に共変的に定数なスピノルが存在することと同値であるため,内部多様体のホロノミーは $SU(3)$ でなければならない.
10次元ヘテロティック弦の超対称性生成子は16個の実成分を持つMajorana–Weylスピノルであり,これらは$Spin(9,1)$の既約表現を成す.群論的には,$SL(2,\mathbb{C})\times SU(4)$の部分群に関して次のように分解される. $$ \bm{16}=(\bm{2},\bm{4})\oplus(\bar{\bm{2}},\bar{\bm{4}}) $$ ここで$SL(2,\mathbb{C})$は4次元のLorentz群に対応するため,$\bm{2}$と$\bar{\bm{2}}$はそれぞれ正・負チャイラリティのWeylスピノルに対応する.内部多様体のホロノミーが$SU(3)$である場合,式(9.56)の$\bm{4}$および$\bar{\bm{4}}$のうち単位表現の成分のみが共変的に定数なスピノルを与える.これらの内部成分を$\eta(y)$などで表すと,共変的に定数なスピノル$\varepsilon$は次のように分解できる. $$ \varepsilon(x,y)=\zeta_+\oplus\eta_+(y)+\zeta_-\oplus\eta_-(y) $$ ここで$\zeta_{\pm}$は$M_4$上の2成分の定数Weylスピノルである.また $$ \eta_-\eta_+^*,\quad \zeta_-=\zeta_+^* $$ が成り立つ.これは$\varepsilon$がMajorana基底であると仮定しているためである.
この $10=4+6$ の分割に都合の良いガンマ行列の表現は $$ \Gamma_{\mu}=\gamma_{\mu}\otimes 1,\quad \Gamma_m=\gamma_5\otimes \gamma_m $$ である.ここで $\gamma_{\mu}$ と $\gamma_m$ はそれぞれ $M_4$ と $M$ のガンマ行列であり,$\gamma_5$ は通常の4次元チャイラリティ演算子 $$ \gamma_5=-i\gamma_0\gamma_1\gamma_2\gamma_3 $$ である.$\gamma_5$ は $\gamma_5^2=1$ を満たし,他の4つの $\gamma$ と反交換する.
内部Dirac行列
内部空間$M$上の$8\times8$ Dirac行列は反対称に選べる.6個の反対称行列で $\{\gamma_i,\gamma_j\}=2\delta_{ij}$ を満たす一例は次の通りである. $$ \sigma_2\otimes 1\otimes \sigma_1,\quad \sigma_2\otimes 1\otimes \sigma_3,\quad \sigma_1\otimes\sigma_2\otimes 1,\quad \sigma_3\otimes\sigma_2\otimes 1,\quad 1\otimes\sigma_1\otimes\sigma_2,\quad 1\otimes\sigma_3\otimes\sigma_2 $$ これら6個すべてと反交換する7番目の反対称行列は $i\gamma_1\gamma_2\cdots\gamma_6$ と定義でき,具体的には $$ \gamma_7=\sigma_2\otimes\sigma_2\otimes\sigma_2 $$ と書ける.チャイラリティ射影演算子は $$ P_{\pm}=(1\pm\gamma_7)/2 $$ である.上で定義した行列を用いて,実基底では $\gamma_m=e^i{}_m\gamma_i$ を定義し,複素基底では $\gamma_a$ と $\gamma_{\bar a}$ を定義する.
Kähler形式と複素構造
ここで,$\eta_+$および$\eta_-$から構成されるフェルミオン二重項を考える. これらのスピノルは共変的に定数であるため,次のように規格化できる. $$ \eta_+^{\dagger}\eta_+=\eta_-^{\dagger}\eta_-=1 $$ 次にテンソルを定義する. $$ J_m{}^n=i\eta_+^{\dagger}\gamma_m{}^n\eta_+=-i\eta_-^{\dagger}\gamma_m{}^n\eta_- $$ これは Fierz transformation formula (given in the appendix of Chapter 10) を用いると次を満たす. $$ J_m{}^nJ_n{}^p=-\delta_m{}^p $$ 結果として,多様体は概複素(almost complex)であり,$J$は概複素構造である.
スピノルと計量が共変的に定数であるため,概複素構造も共変的に定数である.つまり $$ \nabla_mJ_n{}^p=0 $$ これにより,概複素構造は複素構造であるための条件を満たす.具体的には $$ N^p{}_{mn}=0 $$ ここで $N^p{}_{mn}$ は Nijenhuis tensor である(付録および Exercise A.4 参照).したがって,局所複素座標 $z^a$ と $\bar z^{\bar a}$ を導入でき,これらの座標に対して $$ J_a{}^b=i\delta_a{}^b,\quad J_{\bar a}{}^{\bar b}=-i\delta_{\bar a}{}^{\bar b},\quad J_a{}^{\bar b}=J_{\bar a}{}^b=0 $$ と書ける.
注意: $$ g_{mn}=J_m{}^kJ_n{}^lg_{kn} $$ であり,これは式(9.70)と合わせると計量が概複素構造に関してヘルミートであることを意味する.さらに式(9.71)は $$ J_{mn}=J_m{}^kg_{kn} $$ が反対称であることを示し,その結果として二形式を定義する: $$ J=\frac{1}{2}J_{mn}dx^m\wedge dx^n $$ Jの成分は計量と次のように対応する: $$ J_{a\bar b}=ig_{a\bar b} $$ Jの重要な性質の一つは閉形式であることであり,実際に $$ dJ=\partial J+\bar{\partial}J=i\partial_ag_{b\bar c}dz^a\wedge dz^b\wedge dz^{\bar c}+i\partial_{\bar a}g_{\bar b\bar c}dz^{\bar a}\wedge dz^{b} \wedge dz^{\bar c}=0 $$ である.これは計量が共変的に定数であり,捩れのない接続を用いていることを考慮すれば明らかである.したがって背景はKählerであり,$J$はKähler形式である.
正則3-形式
ここでまず $\eta_-$ に関するフェルミオン二重項を考える.$\eta$ は Grassmann 偶数であることを思い出すと,対称性により $\eta_-^{T}\gamma_a\eta_-$ や $\eta_-^{T}\gamma_{ab}\eta_-$ は消える.またチャイラリティにより $\eta_-^{T}\eta_-$ も消える.チャイラリティと対称性の両方と整合する唯一の非零な可能性は $$ \Omega_{abc}=\eta_-^{T}\gamma_{abc}\eta_- $$ である.これを用いて,零点を持たない $(3,0)$-形式を定義できる: $$ \Omega=\frac{1}{6}\Omega_{abc}dz^a\wedge dz^b\wedge dz^c $$
- まず $\Omega$ が閉であることを示す.$\eta$ と計量が共変的に定数であるため,$\nabla_d\Omega_{abc}=0$ を満たす.Kähler 多様体では接続項が消えるため,$\bar{\partial}\Omega=0$ が従う.ホロモルフィック次元が3しかないため $\partial\Omega=0$ であることも明らかであり,したがって $d\Omega=(\partial+\bar{\partial})\Omega=0$ となる.$\bar{\partial}\Omega=0$ であることは係数 $\Omega_{abc}$ がホロモルフィックであることを意味する.
- 一方で $\Omega$ は完全形式ではない.これは $\Omega\wedge\bar{\Omega}$ が体積形式に比例し,その積分が多様体 $M$ 上で非零となるため理解できる(Exercise 9.8 参照).したがって $\Omega\wedge\bar{\Omega}$ は完全形式ではなく,ゆえに $\Omega$ 自身も完全形式ではない.Calabi–Yau 多様体では $h^{3,0}=1$ であり,$\Omega$ は一意的な $(3,0)$ コホモロジー類の代表元である.他の代表元は非零の乗法定数で異なるだけである.
正則な$(3,0)$-形式の存在は,その多様体の第1Chern類が消えることを意味する.実際,正則インデックスは3つの値を取り得るため,$\Omega_{abc}$ は Levi-Civita 記号 $\varepsilon_{abc}$ に比例する. $$ \Omega_{abc}=f(z)\varepsilon_{abc} $$ ここで $f(z)$ は $z^1, z^2, z^3$ に関するどこでも零にならない正則関数である.これにより,ノルムを次のように定義すると $$ ||\Omega||^2=\frac{1}{3!}\Omega_{abc}\bar{\Omega}^{abc} $$ 次が成り立つ. $$ \sqrt{g}=\frac{|f|^2}{||\Omega||^2} $$ ここで $g$ は計量の行列式である.したがってリッチ形式は $$ \mathcal{R}=i\partial\bar{\partial}\log\sqrt{g}=-i\partial\bar{\partial}\log||\Omega||^2 $$ と書ける.$\log||\Omega||^2$ は座標スカラーであり大域的に定義されるため,$\mathcal{R}$ は完全形式となり $c_1=0$ が従う.内部空間はKähler多様体でかつ第1Chern類が消えるので,定義により Calabi-Yau 多様体である.
要約すると,$H=0$ かつディラトンが定数であると仮定すると,ヘテロティック弦を四次元にコンパクト化した際に未破れの $N=1$ 超対称性を要求する条件は,内部多様体が Kähler で第1Chern類が消えることである.言い換えれば,それは Calabi-Yau three-fold である.そのような多様体は一意的な Ricci 平坦計量を持つ.Ricci 平坦計量は一般に本稿で解析した超重力近似の下で選ばれるが,stringy な補正により Ricci 平坦でない計量に変形され得る. この定式化の利点は,第1Chern類が消える Kähler 多様体が様々な方法で構成可能である点にある(そのいくつかは Section 9.3 に示す).しかしながら,ホロノミーのみが指定される背景,今回の例では $SU(n)$ は扱うのが極めて困難である.
Calabi-Yau多様体の変形
特定のHodge数を持つCalabi-Yau多様体は一意ではない.形状や大きさを特徴づけるパラメータ(モジュライ)を変形することで滑らかに結びつくものがあり,しばしば多様体の全モジュライ空間が単一のCalabi-Yau空間として扱われるが,実際には連続的に無限個の多様体の族である.この解釈は,Calabi-Yau多様体の個数が有限かどうかという問いを提起した際に暗黙に想定されていた. Hodge数(例えば $h^{p,q}$)だけでは位相を完全に特徴づけられないため,同じHodge数を持ちながら位相的に異なり,モジュライ空間が互いに分離している複数のCalabi-Yau多様体が存在し得る. 他方で,超重力近似を越えた議論においては,Section 9.8で述べられているconifold 転移のように,Hodge数さえ変えるような滑らかな位相変化(topology-changing transition)を識別できる場合がある.
この節および次の節では,モジュライが4次元における質量ゼロスカラー場の期待値の取り得る未決定な選択肢の空間をどのようにパラメータ化するかを説明する.これらの期待値が未決定であるのは,少なくとも主たる超重力近似において有効ポテンシャルがそれらに依存しないからである.Calabi-Yau three-fold のモジュライ空間の極めて重要な性質は,それが2つの因子の直積になっていることであり,1つは複素構造モジュライを記述し,もう1つは Kähler 構造モジュライを記述する.
ここで,固定されたHodge数を持つ与えられたCalabi-Yau多様体の周りのゆらぎのスペクトルを考える.これらのゆらぎのうちいくつかは計量の変形に由来し,残りは反対称テンソル場の変形から生じる.
反対称テンソル場の変形
Chapter 8で述べたように,低エネルギーのeffective actionは様々な$p$-form場を含み,その運動項は $$ \int d^{10}x\sqrt{-g}|F_p|^2 $$ に比例する.ここで$F_p=dA_{p-1}$である.例えばこの種の場の例としてtype IIAやtype IIBの三形式$H_3=dB_2$がある.この場の方程式は $$ \Delta B_{p-1}=d\star dB_{p-1}=0 $$ である.
直積空間 $M_4 \times M$ 上で4次元にコンパクト化すると,$M$ が Calabi-Yau three-fold の場合,時空の計量は4次元成分と6次元成分の和になる.したがってラプラシアンも2つの項の和となり, $$ \Delta=\Delta_4+\Delta_6 $$ 内部ラプラシアン $\Delta_6$ の零モードの個数が,質量ゼロの4次元場の個数を与える.これらの零モードは Betti 数 $b_p$ によって数えられる.例えば10次元場 $B_2$ は,4次元では2形式,1形式,0形式の場に対応し得る.これらの場の個数は次の表にまとめられている.
| $B_{MN}$ | $p$-form in 4D | $\sharp$ of fields in 4D |
|---|---|---|
| $B_{\mu\nu}$ | $p=2$ | $b_0=1$ |
| $B_{\mu n}$ | $p=1$ | $b_1=0$ |
| $B_{mn}$ | $p=0$ | $b_0=h^{1,1}$ |
この例における $b_2$ のスカラー場は,$B$-場に由来するモジュライである.一般に,$p$-form 場は $b_p$ 個のモジュライ場を生じる.
計量の変形
10次元計量(あるいはグラビトン場)の零モードは,4次元の計量 $g_{\mu\nu}$ と,内部成分 $g_{mn}$ に由来する一連の質量ゼロスカラー場を生じさせる.Calabi-Yau コンパクト化では $b_1 = 0$ であるため,計量から質量ゼロのベクトル場は生成されない.これと密接に関連する事実として,Calabi-Yau three-fold は連続的な等長群を持たない.
内部空間の計量のゆらぎは,小さな変分を施して解析する.すなわち $$ g_{mn} \to g_{mn}+\delta g_{mn} $$ とし,新しい背景が引き続きCalabi-Yau条件を満たすことを要求する.特に $$ R_{mn}(g+\delta g)=0 $$ を満たすことが必要である.これにより $\delta g$ に対する微分方程式が導かれ,その解の個数が超対称性と位相を保ちながら計量を変形できる独立な方法の数を与える.これら独立解の係数がモジュライであり,質量ゼロのスカラー場であるモジュライ場の期待値に対応する.これらのモジュライは内部のCalabi-Yau多様体の大きさや形状の変化をパラメータ化し,位相は変えない.
単純な例:トーラス
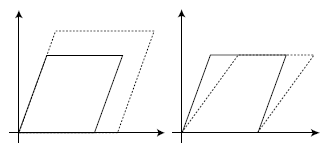
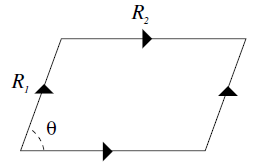
図9.4に示す長方形トーラス $T^2 = S^1 \times S^1$ を考える.このトーラスは平坦計量で記述される.Exercise 9.9 で述べたように,トーラスは2つの複素パラメータ $ \tau $ と $ \rho $ を用いて表すのが便利であり,本例ではこれらは2つの半径と次のように関係する: $$ \tau=i\frac{R_2}{R_1},\quad \rho=iR_1R_2 $$ トーラスの形状,すなわち複素構造は $ \tau $ によって表され,サイズは $ \rho $ によって表される.結果として,トーラスをトーラスのまま保つ変換が2種類存在する.複素構造の変形は $ \tau $ を変え,Kähler構造の変形は $ \rho $ を変える.これらの変形は図9.5に示されている.
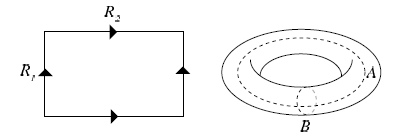
トーラス上の正則1形式は次で与えられる. $$ \Omega=dz $$ 複素構造パラメータ$\tau$は2つの周期の商として表される. $$ \tau=\frac{\int_{A}\Omega}{\int_B\Omega} $$ ここで$A$と$B$は図9.4に示したサイクルである.この定義は次節でCalabi-Yau three-foldへ一般化される. 長方形トーラスは最も一般的なトーラスではない.図9.6に示すように角度が存在し得る. もし$\tau$が実部を持つ場合,mirror symmetry[17]が意味を持つためには$\rho$も実部を持つ必要がある. $\rho$の虚部は体積を記述し,実部は$B$-場に由来する.これはExercise 7.8で説明されている.
Calabi-Yau three-foldsの変形
Calabi-Yau three-fold の計量変形を解析するために,この節序論で概説した戦略を用い,$g_{mn}$ と $g_{mn} + \delta g_{mn}$ がともに Calabi-Yau 条件を満たすことを要求する.特に,これらは Ricci-flat な背景を記述するため,次が成り立つ. $$ R_{mn}(g)=0,\quad R_{mn}(g+\delta g)=0 $$ 一部の計量変形は座標変換を記述しているにすぎず,物理的に興味がない.これらを除くためにゲージを固定する. $$ \nabla^m\delta g_{mn}=\frac{1}{2}\nabla_n\delta g_m{}^m $$ ここで $\delta g_m{}^m = g^{mp}\delta g_{mp}$ である.(9.90) の第二式を $\delta g$ の一次の項で展開し,$g$ の Ricci-flat 性を用いると次が得られる. $$ \nabla^k\nabla_k\delta g_{mn}+2R_m{}^{p}{}_n{}^q\delta g_{pq}=0 $$ この方程式は Lichnerowicz 方程式として知られており,Problem 9.7 で確かめよとある.Kähler 多様体の計量と Riemann テンソルの添字構造の性質を用いると,混成成分 $\delta g_{a\bar b}$ に対する方程式と純成分 $\delta g_{ab}$ に対する方程式とがデカップルすることが分かる.
無限小な$(1,1)$型微分形式 $$ \delta g_{a\bar b}dz^a\wedge d\bar{z}^{\bar b} $$ は,式(9.92)を満たすとき調和である.これは問題9.8で確かめるよう求められている.変分後の$g+\delta g$が古典幾何学において正定値であるべきKähler計量になると仮定する.Kähler計量はKähler形式$J = i g_{a\bar b}dz^a\wedge d\bar{z}^{\bar b}$を定義し,計量の正定性は次と同値である. $$ \int_{M_r}\overbrace{J\wedge\cdots\wedge J}_{r-times}>0,\quad r=1,2,3 $$ ここで$M_r$はCalabi-Yau three-foldの任意の複素$r$次元部分多様体である.式(9.94)を満たすKähler形式を与える計量変形の部分集合をKählerコーンと呼ぶ.この空間はコーンである.なぜなら$J$が式(9.94)を満たすならば,任意の正の数$r$に対して$rJ$もまた満たすからである.図9.7に示す通り.
5つの10次元超弦理論はいずれもNS-NS二形式$B$を含む.Calabi-Yau three-fold上でコンパクト化すると,内部の$(1,1)$型成分$B_{a\bar b}$は$h^{1,1}$個の零モードを持ち,その数だけ追加の質量ゼロスカラー場が4次元に現れる.実閉二形式$B$はKähler形式$J$と結合して複素化されたKähler形式を与える. $$ \mathcal{J}=B+iJ $$ この形式の変動は4次元で$h^{1,1}$個の質量ゼロ複素スカラー場を生じる.したがって,幾何学的にはKähler形式は実であるが,弦理論の文脈では事実上複素化され,トーラスの$\theta$パラメータの複素化を一般化している.この手続きはKählerコーンの複素化と呼ばれる.後で議論するM-theoryのコンパクト化の場合は二形式$B$が存在しないため,Kähler形式および対応するモジュライ空間は複素化されない.
純粋に正則な計量成分 $g_{ab}$ と反正則な成分 $g_{\bar a\bar b}$ は零である.しかし,これらを非零に変化させることで複素構造を変化させることができる.そのような各変分に対して,次の複素$(2,1)$型の形式を対応させることができる. $$ \Omega_{abc}g^{c\bar d}\delta g_{\bar d\bar e}dz^a\wedge dz^b\wedge d\bar z^{\bar e} $$ この形式は式(9.90)が満たされていれば調和形式となる.複素構造変形との厳密な関係は Section 9.6 で説明する.
特殊幾何学
Calabi-Yauのモジュライ空間を記述するために必要な数学は,special geometryとして知られる.本節でその内容を説明する.
モジュライ空間上の計量
モジュライ空間には自然に定まる計量が存在する,それは2つの項の和として与えられる.最初の項は複素構造の変形に対応し,2番目の項は複素化されたKähler形式の変形に対応する. $$ ds^2=\frac{1}{2V}\int g^{a\bar b}g^{c\bar d}[\delta g_{ac}\delta g_{\bar{b}\bar{d}}+(\delta g_{a\bar{d}}\delta g_{c\bar{b}}-\delta B_{a\bar{d}}\delta B_{c\bar{b}})]\sqrt{g}d^6x $$ ここで $V$ は Calabi-Yau 多様体 $M$ の体積である.このように計量が2つの項に分かれることは,少なくとも局所的にはモジュライ空間の幾何が直積構造を持つことを意味する. $$ \mathcal{M}(M)=\mathcal{M}^{2,1}(M)\times\mathcal{M}^{1,1}(M) $$ これらの各因子は,以下で述べるようにそれぞれ興味深い幾何構造を持つ.
複素構造モジュライ空間
Kählerポテンシャル
まず計量の複素構造変形空間から始める. 最初に$(2,1)$型の形式の族を次のように定義する. $$ \chi_{\alpha}=\frac{1}{2}(\chi_{\alpha})_{ab\bar{c}}dz^a\wedge dz^b\wedge d\bar{z}^{\bar{c}},\quad (\chi_{\alpha})_{ab\bar{c}}=-\frac{1}{2}\Omega_{ab}{}^{\bar{d}}\frac{\partial g_{\bar{c}\bar{d}}}{\partial t^{\alpha}} $$ ここで $t^{\alpha}$($\alpha=1,\ldots,h^{2,1}$)は複素構造モジュライ空間の局所座標である. 添字はエルミート計量で上下されるため,例えば $\Omega_{ab}{}^{\bar{d}}=g^{c\bar{d}}\Omega_{abc}$ のようになる. 式(9.96)と同様にこれらの形式は調和である. これらの関係は反転でき,複素構造の変形に伴って計量成分が次のように変わることを示す. $$ \delta g_{\bar{a}\bar{b}}=-\frac{1}{||\Omega||^2}\bar{\Omega}_{\bar{a}}{}^{cd}(\chi_{\alpha})_{cd\bar{b}}\delta t^{\alpha},\quad ||\Omega||^2=\frac{1}{6}\Omega_{abc}\bar{\Omega}^{abc} $$ モジュライ空間上の計量を $$ ds^2=2G_{\alpha\bar{\beta}}\delta t^{\alpha}\delta\bar{t}^{\bar{\beta}} $$ と書き,式(9.97)および式(9.100)から $\delta g_{a\bar b}$ を用いると,モジュライ空間の計量は次のようになる. $$ G_{\alpha\bar{\beta}}\delta t^{\alpha}\delta\bar{t}^{\bar{\beta}}=-\left( \frac{i\int\chi_{\alpha}\wedge\bar{\chi}_{\bar{\beta}}}{i\int\Omega\wedge\bar{\Omega}} \right)\delta t^{\alpha}\delta\bar{t}^{\bar{\beta}} $$
複素構造の変化の下では,正則な$(3,0)$-形式$\Omega$は,$dz$が$dz$と$d\bar{z}$の線形結合になるため,$(3,0)$型と$(2,1)$型の形式の線形結合になる.より正確には, $$ \partial_{\alpha}\Omega=K_{\alpha}\Omega+\chi_{\alpha} $$ ここで$\partial_{\alpha}=\partial/\partial t^{\alpha}$であり,$K_{\alpha}$は局所座標$t^{\alpha}$に依存するがCalabi-Yau多様体$M$上の座標には依存しない.$K_{\alpha}$の具体的な形は以下で決定される.さらに,$\chi_{\alpha}$はまさに(9.99)で定義された$(2,1)$型の形式である.Exercise 9.10は式(9.103)を検証する.
式(9.102)と式(9.103)を組み合わせ,$G_{\alpha\bar{\beta}}=\partial_\alpha\partial_{\bar{\beta}}K$ を思い出すと,複素構造モジュライ空間上の計量がKähler計量であり,そのKählerポテンシャルが次式で与えられることがわかる. $$ \mathcal{K}^{2,1}=-\log\left( i\int\Omega\wedge\bar{\Omega} \right) $$ Exercise 9.9では,2次元トーラスの単純な例を考え,$\Omega=dz$ の場合にKählerポテンシャルが式(9.104)で与えられることを示す.
特殊な座標系
複素構造モジュライ空間をより詳しく記述するため,三次元サイクルの基底 $A_I, B_J$ を導入する.ここで $I,J=0,\ldots,h^{2,1}$ とする.これらの交差数は次を満たすように選ぶ. $$ A^I\cap B_J=-B_J\cap A^I=\delta^I_J,\quad A^I\cap A^J=B_I\cap B_J=0 $$ 双対コホモロジー基底は $(\alpha_I,\beta^I)$ と表す.このとき $$ \int_{A^J}\alpha_I=\int \alpha_I\wedge \beta^J=\delta^J_I,\quad \int_{B_J}\beta^I=\int \beta^I\wedge \alpha_J=-\delta^I_J $$ これらの性質を保存する変換群はシンプレクティックモジュラー群 $Sp(2h^{2,1}+2,\mathbb{Z})$ である.
トーラスの例に類推して,正則な3形式のA周期を用いてモジュライ空間の座標$X^I$を定義できる. $$ X^I=\int_{A^I}\Omega,\quad I=0,\ldots,h^{2,1} $$ このように定義される座標の個数はモジュライ場の個数より1つ多い.しかし,正則な3形式は全体的な複素スケーリングについて一意でないため,座標$X^I$は複素スケーリングに対してのみ定まる.この因子を取り除くために,商 $$ t^{\alpha}=\frac{X^{\alpha}}{X^0},\quad \alpha=1,\ldots,h^{2,1} $$ を考える.ここで添字$\alpha$は0を除く.これにより複素構造モジュライを記述するのに必要な正しい個数の座標が得られる. $X^I$がモジュライ空間を張るのに必要な座標数を与えるので,B周期 $$ F_I=\int_{B_I}\Omega $$ は$X$の関数でなければならない,すなわち$F_I=F_I(X)$である.従って $$ \Omega=X^I\alpha_I-F_I(X)\beta^I $$ が成り立つ.式(9.103)の単純な帰結として $$ \int\Omega\wedge\partial_{I}\Omega=0 $$ があり,これより $$ F_I=X^J\frac{\partial F_J}{\partial X^I}=\frac{1}{2}\frac{\partial}{\partial X^I}(X^JF_J) $$ または同値に $$ F_I=\frac{\partial F}{\partial X^I},\quad F=\frac{1}{2}X^IF_I $$ が得られる.したがって,全てのB周期は一つの関数$F$(プレポテンシャル)の導関数として表される.さらに $$ 2F=X^I\frac{\partial F}{\partial X^I} $$ から$F$は次数2の同次関数であり,座標を係数$\lambda$で拡大すると $$ F(\lambda X)=\lambda^2F(X) $$ が成り立つ.prepotentialは全体的なスケーリングでしか定まらないため,厳密には関数というよりモジュライ空間上の線束の切断である.
プレポテンシャルはモジュライ空間上の計量を決定する.閉じた3形式間の一般的な規則 $$ \int_{M}\alpha\wedge\beta=-\sum_{I}\left( \int_{A^I}\alpha\int_{B_I}\beta-\int_{A^I}\beta\int_{B_I}\alpha \right) $$ を用いると,Kählerポテンシャル(9.104)は次の形に書き直せる. $$ e^{-\mathcal{K}^{2,1}}=-i\sum_{I=0}^{h^{2,1}}(X^I\bar{F}_I-\bar{X}^IF_I) $$ (演習問題でこれを確かめよとある).したがってKählerポテンシャルは,2次同次の正則関数であるプレポテンシャル$F$によって完全に決定される.この型の幾何学は特殊幾何学と呼ばれる.
モジュライ空間の直積構造(9.98)の重要な帰結の一つは,複素構造プレポテンシャル$F$が弦結合定数の零次(ツリー準位)で厳密であることである.実際,その零次展開はCalabi–Yauの体積$V$に関する展開であり,$V$は$\mathcal{M}^{1,1}(M)$に属し,$\mathcal{M}^{2,1}(M)$すなわち複素構造上の位置には依存しない.鏡像対称性と組み合わせると,この重要な事実は複素構造モジュライ空間のみを用いた古典的な幾何学的計算から,Kähler構造モジュライに関わる弦による$\alpha'$補正の無限級数への洞察を与える.
Kähler変換
正則な$(3,0)$-形式$\Omega$は関数$f$によってのみ定まる.この$f$はモジュライ空間の座標$X^I$に依存してもよいが,Calabi-Yauの座標には依存してはならない.すなわち変換 $$ \Omega \to e^{f(X)}\Omega $$ は新たな物理をもたらさない.この変換はKähler計量を変えない.式(9.118)の下で $$ \mathcal{K}^{2,1}\to\mathcal{K}^{2,1}-f(X)-\bar{f}(\bar{X}) $$ となり,これはKähler変換であってKähler計量を不変に保つ.
式(9.103)と(9.104)から$K_{\alpha}$は次のように定まる. $$ K_{\alpha}=-\partial_{\alpha}\mathcal{K}^{2,1} $$ これにより共変微分を導入できる. $$ \mathcal{D}_{\alpha}=\partial_{\alpha}+\partial_{\alpha}\mathcal{K}^{2,1} $$ そして $$ \chi_{\alpha}=\mathcal{D}_{\alpha}\Omega $$ と書ける.この$\chi_{\alpha}$は$\Omega\to e^{f(X)}\Omega$の下で同じ因子$e^{f(X)}$のもとで変換する.
Kähler構造モジュライ空間
Kählerポテンシャル
(1,1) コホモロジー類の空間上の内積は次で定義される. $$ G(\rho,\sigma)=\frac{1}{2V}\int_M\rho_{a\bar{d}}\sigma_{\bar{b}c}g^{a\bar{b}}g^{c\bar{d}}\sqrt{g}\,d^6x=\frac{1}{2V}\int_M\rho\wedge\star\sigma $$ ここで $\star$ は Calabi-Yau 上の Hodge スター作用素を表し,$\rho$ と $\sigma$ は実の $(1,1)$ 型形式である.次に三次形式を定義する. $$ \kappa(\rho,\sigma,\tau)=\int_M\rho\wedge\sigma\wedge\tau $$ Exercise 9.1 から $\kappa(J,J,J)=6V$ であることを思い出せ.恒等式 $$ \star\sigma=-J\wedge\sigma+\frac{1}{4V}\kappa(\sigma,J,J)J\wedge J $$ を用いると,計量は次の形に書き換えられる. $$ G(\rho,\sigma)=-\frac{1}{2V}\kappa(\rho,\sigma,J)+\frac{1}{8V^2}\kappa(\rho,J,J)\kappa(\sigma,J,J) $$
実の調和$(1,1)$型形式の基底を$e_{\alpha}$と表すと,次のように展開できる. $$ \mathcal{J}=B+iJ=w^{\alpha}e_{\alpha},\quad \alpha=1,\ldots,h^{1,1} $$ モジュライ空間上の計量は次のようになる. $$ G_{\alpha\bar{\beta}}=\frac{1}{2}G(e_{\alpha},e_{\beta})=\frac{\partial}{\partial w^{\alpha}}\frac{\partial}{\partial \bar{w}^{\bar{\beta}}}\mathcal{K}^{1,1} $$ ここで $$ e^{-\mathcal{K}^{1,1}}=\frac{4}{3}\int J\wedge J\wedge J=8V $$ 右辺の正規化を変えることは,Kählerポテンシャルを取るに足らない定数だけ平行移動させることに対応する.これらの式は,$w^{\alpha}$によって張られる空間がKähler多様体であることを示し,KählerポテンシャルがCalabi-Yauの体積の対数で与えられることを示す.
交差数を次のように定義する. $$ \kappa_{\alpha\beta\gamma}=\kappa(e_{\alpha},e_{\beta},e_{\gamma})=\int e_{\alpha}\wedge e_{\beta}\wedge e_{\gamma} $$ これらを用いて次を定義する. $$ G(w)=\frac{1}{6}\frac{\kappa_{\alpha\beta\gamma}w^{\alpha}w^{\beta}w^{\gamma}}{w^0}=\frac{1}{6w^0}\int \mathcal{J}\wedge\mathcal{J}\wedge\mathcal{J} $$ これは複素構造モジュライ空間のプレポテンシャルに類似している.ここで $G(w)$ を2次の同次関数にするために,追加の座標すなわち $w^0$ を導入した.すると次が得られる. $$ e^{-\mathcal{K}^{1,1}}=i\sum_{A=0}^{h^{1,1}}\left( w^A\frac{\partial\bar{G}}{\partial \bar{w}^A}-\bar{w}^A\frac{\partial G}{\partial w^A} \right) $$ ここで新しい座標 $w^0$ も和に含まれている.式(9.132)では右辺が $w^0 = 1$ で評価されることが了解されている.演習問題として式(9.132)が式(9.129)と一致することを確かめよ.
プレポテンシャルの形式
先の順でプレポテンシャルは式(9.131)で与えられる.しかし,Calabi-Yauの大きさは$\mathcal{M}^{1,1}(M)$に属するため,$\alpha'$補正が生じ得る.したがって式(9.131)はあくまで先導的な結果に過ぎない.とはいえ補正は完全に任意ではなく,対称性によって制約される.まず$w^{\alpha}$の実部はゲージ変換を持つ$B$によって決定されることに注意せよ.これは場の定数シフトによるPeccei-Quinn対称性を導く.すなわち $$ \delta w^{\alpha}=\varepsilon^{\alpha} $$ である.また$G(w)$が2次同次であることと合わせると,摂動的補正は次の形を取ることが示される. $$ G(w)=\frac{\kappa_{ABC}w^Aw^Bw^C}{w^0}+i\mathcal{Y}(w^0)^2 $$ ここで$\mathcal{Y}$は定数である.$(w^0)^2$の係数は純虚数とみなされる.実数成分はKählerポテンシャルに影響を与えないため自明である.この結果はmirror symmetryを用いて導かれ, $$ \mathcal{Y}=\frac{\zeta(3)}{2(2\pi)^3}\chi(M) $$ となる.ここで$\chi(M)=2(h^{1,1}-h^{2,1})$は多様体のEuler標数である.
非摂動的には状況が変わる,Peccei–Quinn対称性が破れ,$w^\alpha$に依存する補正が可能になる. その結果,次の形の指数関数的に抑圧された寄与の和が生成されることが分かる. $$ \exp\left( -\frac{c_{\alpha}w^{\alpha}}{\alpha'w^0} \right) $$ ここで$c_\alpha$は定数である.これらの補正はインスタントンによって生じる.詳細はSection 9.8で議論している.
Calabi-Yau three-fold上のtype IIA/IIB
type IIAまたはtype IIB超弦理論をCalabi-Yau three-fold $M$上でコンパクト化すると,4次元理論では$\mathcal{N}=2$超対称性が得られる. 計量摂動や他のスカラーゼロモードは,$\mathcal{N}=2$超対称性を持つモジュライ場となる. これらの超対称性を持つモジュライ場は,ベクトル多重項またはハイパー多重項に属する. なぜなら,スカラー場を含む質量のない$\mathcal{N}=2$超対称性の多重項は,この2種類しか存在しないからである.
$D=4$,$\mathcal{N}=2$超多重項
質量のない4次元超多重項は,超代数から容易に導出できる構造を持つ.これは,質量のある場合の解析の質量ゼロ版に対応する.物理状態はヘリシティでラベル付けされ,これは質量のない状態に対してLorentz不変量となる.$\mathcal{N}$拡張超対称性の場合,多重項は最大ヘリシティによって決まり,他の状態の縮重度は二項係数で与えられる.多重項がTCP自己共役でない場合は,共役多重項も加える必要がある[21].
$\mathcal{N}=2$の場合,最大ヘリシティ2の超多重項はヘリシティ3/2の状態が2つ,ヘリシティ1の状態が1つ含まれることになる.TCP共役多重項(ヘリシティが逆のもの)を加えると,$\mathcal{N}=2$超重力多重項となり,1つのグラビトン,2つのグラビティーノ,1つのグラビフォトンが含まれる.最大ヘリシティが1の場合もTCP共役を加えると,同様の議論から$\mathcal{N}=2$ベクトル多重項となり,1つのベクトル,2つのゲージノ,2つのスカラーが含まれる.最後に,最大ヘリシティ1/2の多重項(ハイパー多重項)は,2つのスピン1/2場と4つのスカラーを含む.これら3つのケースはいずれも,ボソン自由度4つとフェルミオン自由度4つを持つ.
type IIA
type IIA理論をCalabi-Yau three-fold $M$上でコンパクト化すると,得られる4次元理論には $h^{1,1}$ 個のアーベルベクトル多重項と $h^{2,1}+1$ 個のハイパー多重項が含まれる.これらの多重項に含まれるスカラー場はモジュライ空間をパラメータ化する.2つのモジュライ空間は混ざり合うことがなく,モジュライ空間は次の直積として表される: $$ \mathcal{M}^{1,1}(M) \times \mathcal{M}^{2,1}(M) $$ 各ベクトル多重項は2つの実スカラー場を含むため,$\mathcal{M}^{1,1}(M)$ の次元は $2h^{1,1}$ となる.この空間には自然に特殊Kähler多様体(正則プレポテンシャルを持つ)としての幾何学が誘導される.各ハイパー多重項は4つの実スカラー場を含むため,$\mathcal{M}^{2,1}(M)$ の次元は $4(h^{2,1}+1)$ となる.この空間は「4元数Kähler多様体」と呼ばれる特殊なタイプとなる[22].これらの幾何学的性質は,$\mathcal{N}=2$超重力とベクトル多重項・ハイパー多重項の相互作用構造から必然的に導かれる.
type IIB
Type IIB理論をCalabi-Yau three-fold $W$上でコンパクト化すると,$h^{2,1}$個のアーベルベクトル多重項と$h^{1,1}+1$個のハイパー多重項が得られる.対応するモジュライ空間は $$ \mathcal{M}^{1,1}(W) \times \mathcal{M}^{2,1}(W) $$ の形となる.この場合,type IIAとは逆で,$\mathcal{M}^{2,1}(W)$が特殊Kähler多様体,$\mathcal{M}^{1,1}(W)$が4元数Kähler多様体となる.
それぞれのtype II理論において,ディラトンは「ユニバーサルハイパー多重項」に属しており,これが各場合で余分なハイパー多重項が現れる理由である.このスカラー場は複素である.なぜなら,もう一つのスカラー場(アクシオン$a$)が存在し,これは4次元で2形式$B_{\mu\nu}$の双対となるからである($dB = \star da$).複素構造モジュライは複素$(2,1)$-形式に対応するため,もともと複素である.$h^{1,1}$個のKählerモジュライも,ヘテロティック弦の場合と同様に,複素化されたKähler形式($J_{ab} + iB_{a\bar{b}}$)の$B$場の寄与によって複素となる.
Calabi-Yauコンパクト化における非摂動的効果
これまで,本稿では第二次超弦革命以前に理解されていたCalabi-Yauコンパクト化の摂動論的側面を議論してきた.本節および続く節では,第二次超弦革命の最中および以後に発見されたCalabi-Yauコンパクト化の非摂動的側面のいくつかを論じる.
コニフォールド特異点
非一意性に加え,Calabi-Yauコンパクト化の主要な問題の一つはモジュライ空間に特異点が含まれることである.すなわち古典的記述が破綻する点が存在するということである.そのような特異点の具体例である conifold singularity を解析することで,古典的な低エネルギー有効作用の記述が破綻することが明らかになった.消失(または縮退)するサイクルに巻かれた brane による非摂動的効果を考慮する必要がある.
具体的には,Type IIB 理論を Calabi-Yau three-fold 上でコンパクト化した場合を考える.前節で示したように,モジュライ空間 $ \mathcal{M}^{2,1}(M) $ は同次特殊座標 $X^I$ で記述できる.conifold 特異点は,ある座標,例えば $$ X^1=\int_{A^1}\Omega $$ が零になると現れる.$A^1$ 上の周期がゼロに近づくため,$A^1$ は消失サイクル(vanishing cycle)と呼ばれる.これらの点では一般にモジュライ空間上の計量が特異になる.実際,部分空間 $X^1=0$ は複素共次元1を持ち,$h^{2,1}=1$ の場合は点に対応するため,閉ループで囲むことができる.そのようなループの周りを解析接続すると,3-サイクルの基底は $Sp(2,\mathbb{Z})$ のモノドロミー変換のもとでしか元に戻らない.一般にモノドロミーは $$ X^1\to X^1,\quad F_1\to F_1+X^1 $$ の形を取る.このことは,conifold 特異点付近で次が成り立つことを示唆する. $$ F_1(X^1)=\text{const}+\frac{1}{2\pi i}X^1\log X^1 $$ 最も単純な場合には他の周期は自明に変換すると仮定できる.この結果は,conifold 特異点付近でKählerポテンシャルが式(9.117)のもとで $$ \mathcal{K}^{2,1}\sim \log(|X^1|^2\log |X^1|^2) $$ の形を取ることを意味する.したがって $$ G_{1\bar{1}}=\partial_{1}\partial_{\bar{1}}\mathcal{K}^{2,1} $$ は $X^1=0$ で特異となる.これは単なる座標特異ではなく実際の特異であり,スカラー曲率が発散することから確認できる.これは課題問題で検証するよう指示されている.
モジュライ空間の特異点は次の理由で生じる.Calabi-Yauコンパクト化は,質量を持つ場を積分除去した低エネルギー有効作用による記述である.conifold特異点では,ある種のもともと質量を持っていた状態が質量ゼロとなり,そのような場を積分除去した仮定と矛盾が生じる.特に,特異点で質量を失う状態は,D3-braneが特定の3次元サイクルを巻くことで生じる.これらのサイクルは special Lagrangian cycles(特殊ラグランジュサイクル)と呼ばれ,次節で説明する.conifold特異点付近ではこれらの状態は軽くなり,低エネルギー有効作用から除外することはもはや整合的でない.
超対称サイクル
この節では,超対称サイクルを巻くユークリッド化ブレーンによる非摂動効果をどのように計算するかを説明する.ユークリッド化された$p$-braneの世界体積は$p+1$次元の空間を持ち,物理的Minkowski時空の時間ではなく世界体積の時間がユークリッド化される点に注意せよ.ユークリッド化された$p$-braneが,ある超対称性を保存するように$(p+1)$-サイクルを巻けるとき,そのサイクルは超対称サイクルと呼ばれる.このとき経路積分に対して非摂動的なインスタントン補正として寄与する.より正確には,fundamental-stringのインスタントンは$\alpha'$に対して非摂動的な寄与を与え,D-braneやNS5-braneは$g_s$に対しても非摂動的な寄与を与える.23 Calabi–Yau three-foldが内部多様体である場合に非自明な$(p+1)$-サイクルが存在し得る$p$の値は $p=-1,1,2,3,5$ である.
Chapter 6で述べたように,type IIA superstring theoryは偶数次元のBPS D-braneを含み,type IIB theoryは奇数次元のBPS D-braneを含む.各D-braneは保存される$R$-$R$電荷を担う.したがって,基礎弦が$2$-cycleを巻く場合やNS5-braneが多様体全体を巻く場合に加え,IIAではD2-braneを$3$-cycleに巻くことが考えられる.同様にIIBではD1,D3,D5-braneやD-instantonを巻くことができる.これらの構成はモジュライ空間の幾何に非摂動的なインスタントン寄与を与え,弦理論が一貫するためにはこれらを含める必要がある.Section 9.9で述べたように,これらの効果はmirror symmetryのような弦理論の基本的性質を理解する上で重要である.Calabi-Yau compactificationsの文脈では,超対称性を保存するサイクルにはいくつかの種類があり,以下で議論する.
特殊Lagrangian部分多様体
M-theoryのCalabi-Yauコンパクト化は低エネルギーで$5$次元の理論を与えるため,考え得るインスタントン構成はM2-braneが$3$-サイクルを巻くものとM5-braneがCalabi-Yau全体を巻くものに限られる.まず,世界体積が3次元であるユークリッド化されたM2-braneを考える.目的は,ユークリッド化された膜がCalabi-Yau上の$3$-サイクルを巻く配置が経路積分の定常点に対応し,かつ超対称性を保存するための条件を解析することである.これが確認できれば,次にその配置が低エネルギーの$5$次元有効作用に与える対応する非摂動的寄与を決定する.
11次元のM2-braneは世界体積上の作用を持ち,global supersymmetryと局所的なkappa対称性を備え,その形式はChapters 5および6で述べたfundamental superstringsやD-branesの作用に類似する.他の例と同様に,この作用は時空において次のglobal supersymmetryの下で不変である. $$ \delta_{\varepsilon}\Theta=\varepsilon,\quad \delta_{\varepsilon}X^M=i\bar{\varepsilon}\Gamma^M\Theta $$ ここで$X^M$($M=0,\ldots,10$)は時空における膜の配置を記述する座標である.$\Theta$は$32$成分のMajoranaスピノルであり,$\varepsilon$は定数の無限小Majoranaスピノルである.しかし,ユークリッド化したM2-braneがコンパクト化空間の3周期を巻いた場合にどの程度の超対称性が残るかという問題が生じる.M2-braneはフェルミオンの局所的なkappa対称性の下でも不変であり,この対称性は場に対して次のように作用する. $$ \delta_{\kappa}\Theta=2P_+\kappa(\sigma),\quad \delta_{\kappa}X^M=2i\bar{\Theta}\Gamma^MP_+\kappa(\sigma) $$ ここで$\kappa(\sigma)$は無限小の$32$成分Majoranaスピノルであり,$P_{\pm}$は直交する射影作用素で次のように定義される. $$ P_{\pm}=\frac{1}{2}\left( 1\pm\frac{i}{6}\varepsilon^{\alpha\beta\gamma}\partial_{\alpha}X^M\partial_{\beta}X^N\partial_{\gamma}X^P\Gamma_{MNP} \right) $$
解析の鍵は,特定の配置 $X^M(\sigma)$(および $\Theta=0$)が,ある $\varepsilon$ に対応する超対称性を保存するのはその変換が $\kappa$ 変換で打ち消せる場合であるという観察にある.言い換えれば,ある $\kappa(\sigma)$ が存在して $$ \delta_{\varepsilon}\Theta+\delta_{\kappa}\Theta=\varepsilon+2P_+\kappa(\sigma)=0 $$ が成り立つ必要がある.ここで $P_+$ に作用させると次が従う. $$ P_-\varepsilon=0 $$ この方程式は次の2つの条件と同値である.
- 11次元座標 $X^M$ は Calabi–Yau の座標を表す $X^a$ と $X^{\bar a}$,および五次元時空の座標 $X^{\mu}$ から構成される.超対称インスタントン解では $X^{\mu}=X^{\mu}_0$ は定数であり,非自明な埋め込みは他の座標に関わる.第一の条件は $$ \partial_{[\alpha}X^a\partial_{\beta]}X^{\bar{b}}J_{a\bar{b}}=0 $$ であり,これは Calabi–Yau three-fold の Kähler 形式の膜世界体積への引き戻しがゼロであることを意味する.
- 第二の条件は $$ \partial_{\alpha}X^a\partial_{\beta}X^b\partial_{\gamma}X^c\Omega_{abc}=e^{-i\varphi}e^{\mathcal{K}}\varepsilon_{\alpha\beta\gamma} $$ である.これは Calabi–Yau 多様体の正則 $(3,0)$ 形式 $\Omega$ の膜世界体積への引き戻しが膜の体積要素に比例することを意味する.その複素共役の式は反正則 $(0,3)$ 形式について同様の条件を与える.位相 $\varphi$ は $\eta$ の定義における任意性を反映する定数である.因子 $e^{\mathcal{K}}$ は便宜的な正規化因子であり, $$ \mathcal{K}=\frac{1}{2}(\mathcal{K}^{1,1}-\mathcal{K}^{2,1}) $$ で与えられる.ここで $\mathcal{K}^{2,1}$ は $h^{2,1}$ 個のハイパー多重項に属する複素モジュライの関数であり,$\mathcal{K}^{1,1}$ は $h^{1,1}$ 個のベクトル超多重項に属する実モジュライの関数である.
式(9.149)および(9.150)で与えられる超対称性を満たす3次元サイクルの条件は,special Lagrangian部分多様体を定義する.これらの条件が満たされると,形 $ \varepsilon = P_+\eta $ の非零の共変的に定数なスピノルが存在する.したがって,Calabi–Yau three-fold の special Lagrangian部分多様体を巻くユークリッド化された M2-brane は,5次元低エネルギー有効理論に超対称性を保つインスタントン寄与を与える.
条件(9.149)および(9.150)は膜が体積を最小化していることを示す.膜の体積に対する下限を導くために,次を考える. $$ \int_{\Sigma}\varepsilon^{\dagger}P_-^{\dagger}P_-\varepsilon d^3\sigma \geq 0 $$ ここで$\Sigma$は膜の世界体積である. $$ P_-^{\dagger}P_-=P_-P_-=P_- $$ よって不等式は次の形となる. $$ 2\mathcal{V}\geq e^{-\mathcal{K}}\left( e^{i\varphi}\int_{\Sigma}\Omega+e^{-i\varphi}\int_{\Sigma}\bar{\Omega} \right) $$ ここで$\varphi$は調整可能な位相であり,これを適切に選ぶと次が得られる. $$ \mathcal{V} \geq e^{-\mathcal{K}}\left| \int_{\Sigma}\Omega \right| $$ この下限は膜が超対称サイクル$\mathcal{C}$を巻くときに飽和し,その場合 $$ \mathcal{V} = e^{-\mathcal{K}}\left| \int_{\mathcal{C}}\Omega \right| $$ となる.
Type IIAまたはType IIBの超弦理論をCalabi-Yau three-fold上でコンパクト化した場合も,同様に超対称サイクルが存在し,それらは同様の方法で決定できる.M-theoryの場合と同様,Type IIA理論はspecial Lagrangian部分多様体を巻くD2-braneに対応するインスタントン寄与を受ける.これらの寄与は結合定数に対して$e^{-1/g_s}$の形で依存する.なぜならD2-braneの張力は$1/g_s$に比例するからである.
ブラックホール質量公式
Type IIB理論をCalabi-Yau three-fold上でコンパクト化すると,特殊ラグランジュ3-サイクルにD3-braneを巻くことで4次元の超対称ブラックホールが実現できる.今回のケースでブラックホールの質量の下界は次の形をとる. $$ M \geq e^{\mathcal{K}{2,1}/2}\left| \int_{\mathcal{C}}\Omega \right|=e^{\mathcal{K}^{2,1}/2}\left| \int_M\Omega\wedge\Gamma \right| $$ ここで$\Gamma$はサイクル$\mathcal{C}$にポアンカレ双対な3-形式である.ここではD3-brane上の質量分布が一様であると仮定している. $$ \Gamma=q^I\alpha_I-p_I\beta^I $$ とおくと,特殊座標を導入し展開(9.110)を用いることでBPS境界 $$ M \geq e^{\mathcal{K}^{2,1}/2}|p_IX^I-q^IF_I| $$ が得られる.BPS状態では不等式は飽和し,質量は超対称代数における中心荷$Z$の絶対値に等しい.したがって式(9.157)は$|Z|$の式ともなる.結果として,あるサイクルが縮んでゼロサイズになるとBPS状態は質量ゼロとなる.中心荷と特殊座標を結ぶ上記の関係式は,Chapter 11で述べるブラックホールのアトラクタ機構の議論で重要な役割を果たす.
正則サイクル
Type II 理論の場合,その他の超対称サイクルも寄与し得る.たとえば,ユークリッド化した Type IIA の世界面がホロモルフィックなサイクルを巻くと,一部の超対称性が保存される.これは埋め込みが $$ \bar{\partial}X^a=0,\quad \partial X^{\bar{a}}=0 $$ に加えて $X = X_0$ を満たすことを意味する.したがってユークリッド化した世界面の複素構造は Calabi-Yau 多様体の複素構造と整合している.この場合,埋め込みはホロモルフィックに埋め込まれていると呼ばれる.Type IIA 理論が円上に compactified された M-theory に対応することを思い出せ.したがって M-theory の観点からは,この例は M4×S1×M 上の解に対応し,ユークリッド化された M2-brane が円と Calabi-Yau のホロモルフィックな2-サイクルを巻いている構成に相当する.
ミラー対称性
T-dualityが示す通り,点粒子が探る幾何学は弦が探る幾何学と異なる.弦幾何学では半径$R$の円が半径$\alpha'/R$の円と同等になり得る.これは弦幾何学の驚くべき性質の簡単な例を示す.Calabi-Yau three-foldsに対する同様の現象はmirror symmetryと呼ばれ,本節で扱う.
脚注
- 末尾の付録に数学的な基礎事項がまとめられている.位相幾何学や幾何学の基礎に慣れていない人は,まずそちらを学習することをおすすめする.▲
- 「対称性」と呼ばれてはいるが,ミラー対称性は実際には双対性であり,Calabi-Yau多様体のペアを関係づけるものである.▲
- 例外として,トーラスや複素平面などがある.▲
- トーラスを除き,ここで考えるCalabi-Yau多様体は単連結である.単連結でないCalabi-Yau多様体は,離散的かつ自由に作用する等長変換群で割ることで構成できる.興味のあるすべての場合,これらの群は有限であり,そのため得られるCalabi-Yau多様体もこの式を満たす.▲
- 一般に,$Sp(n)$ホロノミーを持つ$4n$次元多様体はハイパーKähler多様体と呼ばれる.$USp(2n)$という記法も,コンパクト型を強調したい場合に同じ群に対して使われる.本書では両方の記法を用いる.▲
- 4次元で自己共役な超多重項は,$\mathcal{N}=4$ベクトル多重項と$\mathcal{N}=8$超重力多重項のみである.▲
- 4元数Kähler多様体はKähler多様体ではないことに注意.定義は補遺に記載されている.▲