ベクトル束
本稿は主に Lee の教科書 [Lee02] に基づいている.また日本語の文献として主に[松本88,中原18]を参考にしている.
滑らかな多様体の接束は,それ自体が自然な滑らかな多様体構造を持つ.接束$TM$上に構成した自然座標系は,局所的に$M$の開部分集合と$\mathbb{R}^n$との直積のように見える.この種の構造は非常によく現れる.すなわち,$M$の各点ごとにベクトル空間が割り当てられ,それらが$M$と$\mathbb{R}^n$の直積のように局所的には貼り合わされているが,大域的には「ねじれている」かもしれないという構造である.このような構造を「ベクトル束」と呼ぶ.
ベクトル束(やファイバー束)に関する理論は非常に深く広範であり,ここではその全貌に触れることはしない.本稿でこれらを導入する主な理由は,接束やそれに類する構造について議論する際に便利な言語を得るためである.滑らかな多様体上にはこのような構造が豊富に存在する.
目次
ベクトル束
ベクトル束
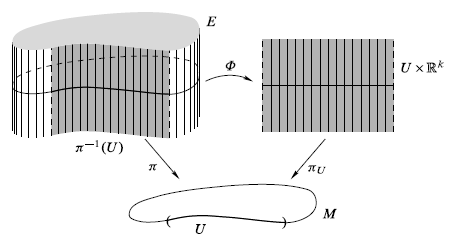
$M$を位相空間とする.$M$上の階数$k$の(実)ベクトル束(vector bundle)とは,位相空間$E$と,$E$から$M$への全射連続写像$\pi: E \to M$の組$(E, \pi)$で,次の条件を満たすものである:
- 各$p \in M$に対し,ファイバー(fiber)$E_p = \pi^{-1}(p)$ には$k$次元実ベクトル空間の構造が入っている.
-
各$p \in M$に対し,$p$の近傍$U \subset M$と,$\pi^{-1}(U)$から$U \times \mathbb{R}^k$への全単射な連続写像$\Phi: \pi^{-1}(U) \to U \times \mathbb{R}^k$($E$の$U$上の局所自明化(local trivialization)と呼ぶ)が存在し,次を満たす(下図参照):
- $\pi_U \circ \Phi = \pi$(ここで$\pi_U: U \times \mathbb{R}^k \to U$は射影)である.
- 各$q \in U$について,$\Phi$の$E_q$への制限は$E_q$から$\{q\} \times \mathbb{R}^k \cong \mathbb{R}^k$へのベクトル空間同型である.
滑らかなベクトル束
$M$および$E$が(境界の有無を問わない)滑らかな多様体であり,$\pi$が滑らかな写像で,局所自明化が微分同相写像として選べるとき(滑らかな局所自明化(smooth local trivialization)と呼ぶ.),$E$を滑らかなベクトル束(smooth vector bundle)という.
特に階数$1$のベクトル束を線束(line bundle)という.
複素ベクトル束(complex vector bundle)も同様に定義されるが,「実ベクトル空間」を「複素ベクトル空間」に,「$\mathbb{R}^k$」を「$\mathbb{C}^k$」に置き換えるだけである.
本稿では複素ベクトル束を扱わないため,特に断りがない限り,すべてのベクトル束は実ベクトル束とする.
ベクトル束の定義において,
- 位相空間$E$をベクトル束の全空間(total space)という.
- 位相空間$M$を底空間(base space)という.
- 写像$\pi: E \to M$を射影(projection)という.
強調したい内容によっては,記法の中でいくつかの要素を省略して「位相空間$E$は位相空間$M$上のベクトル束である」や「写像$E \to M$はベクトル束である」,あるいは「射影$\pi: E \to M$はベクトル束である」などと書くこともある.
自明束
底空間$E$全体にわたる局所自明化(大域自明化(global trivialization)という)が存在する場合,$E$は自明束(trivial bundle)であるという.特に$E \to M$が滑らかなベクトル束であり,滑らかな大域自明化を持つ場合,$E$は滑らかに自明(smoothly trivial)であるという.
(滑らかな)自明束の底空間$E$は直積空間$M \times \mathbb{R}^k$と(微分)同相になる.
簡単のため,本稿で「滑らかな束が自明である」と言うときは,常に「滑らかに自明である」ことを意味し,位相的な意味での自明ではないことに注意する.
階数$k$のベクトル束の特に単純な例として,任意の空間$M$上の直積空間$E = M \times \mathbb{R}^k$を考えることができる.射影$\pi: M \times \mathbb{R}^k \to M$を用いる.このような束は直積束(product bundle)と呼ばれ,自明束である(恒等写像が大域自明化となる).$M$が(境界の有無を問わない)滑らかな多様体であれば,$M \times \mathbb{R}^k$は滑らかに自明である.//
自明でないベクトル束は多数存在するが,視覚的に理解しやすい唯一の例は次のものである.
$\mathbb{R}^2$上に次の同値関係を定める:$(x, y) \sim (x', y')$であるとは,ある$n \in \mathbb{Z}$が存在して$(x', y') = (x + n, (-1)^n y)$となることをいう.$E = \mathbb{R}^2 / \sim$をこの同値関係による商空間とし,$q: \mathbb{R}^2 \to E$を商写像とする.
商空間$E$を視覚化するために,$S$を帯$[0,1] \times \mathbb{R}\subset\mathbb{R}^2$とする.$q$の$S$への制限は全射かつ閉写像なので,これは商写像である.$q|_S$による唯一の非自明な同一視は,2つの境界線上で行われるため,$E$は,右端に半回転を加えて上下を逆にし,左端と貼り合わせることで得られる空間と考えることができる(下図参照).任意の$r > 0$に対して,矩形$[0,1] \times [-r, r]$の商写像$q$の像は,境界を持つ滑らかなコンパクト多様体であり,これをMöbiusの帯(Möbius band)と呼ぶ.紙の帯の両端を半回転させて貼り合わせることで,この空間の模型を作ることができる.
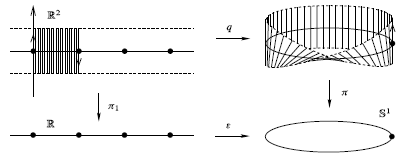
次の可換図式を考える: $$ \begin{CD} \mathbb{R}^2 @>q>> E \\ @V{\pi_1}VV @VV{\pi}V \\ \mathbb{R} @>>{\varepsilon}> \mathbb{S}^1 \end{CD} $$ ここで$\pi_1$は第1成分への射影,$\varepsilon: \mathbb{R} \to \mathbb{S}^1$は滑らかな被覆写像$\varepsilon(x) = e^{2\pi ix}$である.$\varepsilon \circ \pi_1$は各同値類上で定数なので,$E$への連続写像$\varepsilon: E \to \mathbb{S}^1$に降下する.直接計算(少し面倒だが)により,$E$には$q$が滑らかな被覆写像となり,$\varepsilon: E \to \mathbb{S}^1$が$\mathbb{S}^1$上の滑らかな実線束(Möbius束という)となるような一意な滑らかな多様体構造が入ることが分かる.//
最も重要なベクトル束の例は接束である:
ベクトル束としての接束
$M$を(境界の有無を問わない)滑らかな$n$次元多様体とし,$TM$をその接束とする.自然な射影写像,各ファイバー上の自然なベクトル空間構造,および以前の命題で構成された位相と滑らかな構造を備えることで,$TM$は$M$上の階数$n$の滑らかなベクトル束となる.
自明でない束は必ず2つ以上の局所自明化が必要となる.次の補題は,2つの滑らかな局所自明化の合成が,重なり合う部分では単純な形になることを示している:
$E \to M$を階数$k$の滑らかなベクトル束とする.$E$の2つの滑らかな局所自明化$\Phi: \pi^{-1}(U) \to U \times \mathbb{R}^k$,$\Psi: \pi^{-1}(V) \to V \times \mathbb{R}^k$があり,$U \cap V \neq \varnothing$とする.このとき,滑らかな写像$\tau: U \cap V \to \mathrm{GL}(k, \mathbb{R})$が存在して,合成$\Phi \circ \Psi^{-1}: (U \cap V) \times \mathbb{R}^k \to (U \cap V) \times \mathbb{R}^k$は $$ \Phi \circ \Psi^{-1}(p, v) = (p, \tau(p) v) $$ の形になる.ここで,$\tau(p) v$は$k \times k$行列$\tau(p)$による通常のベクトル$v \in \mathbb{R}^k$への作用を表す.
変換関数
上の補題で現れる$U \cap V \to \mathrm{GL}(k, \mathbb{R})$の滑らかな写像を,局所自明化$\Phi$と$\Psi$の間の変換関数(transition function)と呼ぶ.
この定義は滑らかな多様体論で「関数」という用語が,値域が$\mathbb{R}$や$\mathbb{R}^k$でない場合に使われる数少ない例の一つである.慣習的にこの用語が使われる.
$M$が滑らかな多様体で,$\Phi$および$\Psi$が$TM$の2つの異なる滑らかなチャートに対応する局所自明化であるとき,それらの間の変換関数は,座標変換写像のJacobi行列になる.//
接束と同様に,ベクトル束も,底多様体の各点ごとにベクトル空間を割り当てる集合として記述するのが最も簡単な場合が多い.このような集合を滑らかなベクトル束にするには,まずすべてのベクトル空間の互いに素な和集合に多様体のための位相と滑らかな構造を入れ,さらに局所自明化を構成し,それらが必要な性質を満たすことを示さなければならない.次の補題はその近道を与えるものであり,あとは局所自明化を構成し,それらが滑らかな変換関数で重なり合うことさえ示せば十分であることを示している:
ベクトル束のチャート補題
$M$を(境界の有無を問わない)滑らかな多様体とし,各$p \in M$に対して,ある固定された次元$k$の実ベクトル空間$E_p$が与えられているとする.$E = \bigsqcup_{p \in M} E_p$とし,$\pi: E \to M$を,各$E_p$の元を点$p$へ写す写像とする.さらに,次のデータが与えられているとする:
- $M$の開被覆$\{U_\alpha\}_{\alpha \in A}$
- 全単射写像$\Phi_\alpha: \pi^{-1}(U_\alpha) \to U_\alpha \times \mathbb{R}^k$で,各$E_p$への制限が$E_p$から$\{p\} \times \mathbb{R}^k \cong \mathbb{R}^k$へのベクトル空間同型となるもの
- $U_\alpha \cap U_\beta \neq \varnothing$となる任意の$\alpha, \beta \in A$について,$U_\alpha \cap U_\beta \to \mathrm{GL}(k, \mathbb{R})$の滑らかな写像$\tau_{\alpha\beta}$で,$\Phi_\alpha \circ \Phi_\beta^{-1}: (U_\alpha \cap U_\beta) \times \mathbb{R}^k \to (U_\alpha \cap U_\beta) \times \mathbb{R}^k$が $$ \Phi_{\alpha} \circ \Phi_{\beta}^{-1}(p,v)=(p,\tau_{\alpha\beta}(p)v) $$ の形になるもの
以下に,チャート補題を用いて新しいベクトル束を構成する例を示す:
滑らかな多様体$M$と,その上の階数$k'$および$k''$の滑らかなベクトル束$E'$,$E''$が与えられたとする.$E'$と$E''$から新しいベクトル束を構成することができ,これを$E' \oplus E''$のWhitney和(Whitney sum)と呼ぶ.各点$p \in M$におけるファイバーは$E'_p \oplus E''_p$(直和)となる.全空間は$E' \oplus E'' = \bigsqcup_{p \in M} (E'_p \oplus E''_p)$であり,自然な射影$\pi: E' \oplus E'' \to M$が定まる.各点$p \in M$について,十分小さい近傍$U$を選び,$E'$および$E''$の局所自明化$(U, \Phi')$および$(U, \Phi'')$を取る.$E' \oplus E''$の局所自明化$\Phi: \pi^{-1}(U) \to U \times \mathbb{R}^{k'+k''}$を $$ \Phi(v', v'') = (\pi'(v'), (\pi_{\mathbb{R}^{k'}} \circ \Phi'(v'), \pi_{\mathbb{R}^{k''}} \circ \Phi''(v''))) $$ で定める.さらに,別の局所自明化の組$(\tilde{U}, \tilde{\Phi}')$, $(\tilde{U}, \tilde{\Phi}'')$を考える.対応する変換関数を$\tau': U \cap \tilde{U} \to \mathrm{GL}(k', \mathbb{R})$,$\tau'': U \cap \tilde{U} \to \mathrm{GL}(k'', \mathbb{R})$とすると,$E' \oplus E''$の変換関数は $$ \tilde{\Phi} \circ \Phi^{-1}(p, (v', v'')) = (p, \tau(p)(v', v'')) $$ となり,ここで $$ \tau(p) = \tau'(p) \oplus \tau''(p) \in \mathrm{GL}(k'+k'', \mathbb{R}) $$ は次のブロック対角行列で与えられる: $$ \begin{pmatrix} \tau'(p) & 0 \\ 0 & \tau''(p) \end{pmatrix} $$ この変換関数は$p$に関して滑らかに依存するので,チャート補題より$E' \oplus E''$は$M$上の滑らかなベクトル束となる.//
ベクトル束の局所切断と大域切断
切断
$\pi:E \to M$をベクトル束とする.$E$の切断(section)とは,射影写像$\pi$の切断,すなわち連続写像$\sigma: M \to E$であって,$\pi \circ \sigma = \mathrm{Id}_M$を満たすものである.
これは,任意の$p \in M$に対して$\sigma(p)$がファイバー$E_p$の元となることを意味する.
局所切断と大域切断
ベクトル束$E$の局所切断(local section)とは,$M$の開部分集合$U$上で定義された連続写像$\sigma: U \to E$であって,$\pi \circ \sigma = \mathrm{Id}_U$を満たすものである.この区別を強調するため,$M$全体で定義された切断を大域切断(global section)と呼ぶことがある.
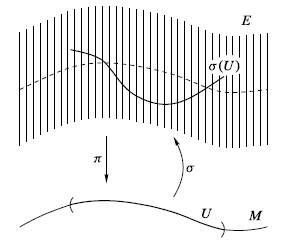
$U \subset M$上の$E$の局所切断は,$E|_U$($E$の$U$への制限束)の大域切断と同じ意味である.
滑らかな切断
$M$が(境界の有無を問わない)滑らかな多様体で$E$が滑らかなベクトル束である場合,滑らかな切断(smooth section)とは,$U \subset M$上の滑らかな写像$\sigma: U \to E$で,$\pi \circ \sigma = \mathrm{Id}_U$を満たすものである.
ベクトル場の場合と同様に,場合によっては「連続性」は仮定せずに,切断の条件を満たす写像を考えることが有用なことがある:
粗い切断
ベクトル束$E$の粗い切断(rough section)とは,$U \subset M$上の写像$\sigma: U \to E$で,必ずしも連続である必要はなく,$\pi \circ \sigma = \mathrm{Id}_U$を満たすものである.
特に断りがない限り,「切断」と言った場合は常に連続な切断を意味するものとする.
ゼロ切断
ベクトル束$E$のゼロ切断(zero section)とは,$M$上の大域切断 $\zeta: M \to E$で,各$p \in M$に対して $$ \zeta(p) = 0 \in E_p $$ で定義されるものである.
切断の台
切断$\sigma$の台(support)とは,$\sigma(p) \neq 0$となる点全体の集合の閉包である.
$M$が(境界の有無を問わない)滑らかな多様体であるとする.ベクトル束の切断の例としては
- $TM$の切断は$M$上のベクトル場である.
- 境界の有無を問わず,$M$の埋め込み部分多様体$S$が与えられたとき,$TM|_S \to S$の切断は$S$に沿ったベクトル場(vector field along $S$)と呼ばれる.これは連続写像$X: S \to TM$で,各点$p \in S$に対して$X_p \in T_pM$となるものである.これは$S$上のベクトル場(各点$p$で$X_p \in T_pS$)とは異なる.
- $E = M \times \mathbb{R}^k$が直積束の場合,$E$の切断と$M$から$\mathbb{R}^k$への連続関数は自然に一対一対応する.すなわち,連続関数$F: M \to \mathbb{R}^k$は切断$\tilde{F}: M \to M \times \mathbb{R}^k$を$\tilde{F}(x) = (x, F(x))$で定め,逆も同様である.$M$が滑らかな多様体なら,切断$\tilde{F}$が滑らかであることと$F$が滑らかであることは同値である.
- 上記の対応により,空間$C^\infty(M)$($M$上の滑らかな関数)と自明線束$M \times \mathbb{R} \to M$の滑らかな切断空間は自然に同一視できる.
$E \to M$が滑らかなベクトル束であるとき,$E$の滑らかな大域切断全体の集合は,点ごとの加法とスカラー倍によってベクトル空間となる: $$ (c_1\sigma_1 + c_2 \sigma_2)(p) \equiv c_1 \sigma_1(p) + c_2 \sigma_2(p) $$ このベクトル空間は通常$\Gamma(E)$で表される.
特定のベクトル束については,その切断空間に特別な記号を導入することも多い.例えば,接束$TM$の滑らかな切断全体の空間には,$\mathfrak{X}(M)$という記号が使われる.
滑らかなベクトル場と同様に,滑らかなベクトル束$E \to M$の滑らかな切断も,滑らかな実数値関数を掛けることができる.すなわち,$f \in C^\infty(M)$,$\sigma \in \Gamma(E)$のとき,新たな切断$f\sigma$ を $$ (f\sigma)(p) \equiv f(p)\sigma(p) $$ で定める.
ベクトル束の拡張補題
$E \to M$を(境界の有無を問わない)滑らかなベクトル束とする.$A \subset M$を閉集合とし,$\sigma: A \to E$を$E|_A$上の切断で,各点の近傍で滑らかな局所切断に拡張できる(すなわち,$\sigma$は$A$上で滑らか)とする.任意の$A$を含む開集合$U \subset M$に対して,$E$の滑らかな大域切断$\tilde{\sigma} \in \Gamma(E)$が存在し,$\tilde{\sigma}|_A = \sigma$かつ$\mathrm{supp}\,\tilde{\sigma} \subset U$となる.
局所枠と大域枠
局所枠の概念は,ベクトル束にも自然に拡張される:
線形独立な切断
$E \to M$をベクトル束とする.$U \subset M$を開集合とし,$E$の$U$上の局所切断の$k$組$\sigma_1, \ldots, \sigma_k$を考える.このとき,各点$p \in U$で,$\sigma_1(p), \ldots, \sigma_k(p)$がファイバー $E_p$で線形独立ならば,$\sigma_1, \ldots, \sigma_k$は$U$上で線形独立(linearly independent)であるという.同様に,各点$p \in U$で$\sigma_1(p), \ldots, \sigma_k(p)$が$E_p$を張るとき,$\sigma_1, \ldots, \sigma_k$は$U$上で$E$を張る(span)という.
局所枠と大域枠
ベクトル束$E$の$U$上の局所枠(local frame)とは,$U$上の局所切断の順序付き$k$組$(\sigma_1, \ldots, \sigma_k)$で,各点$p\in U$について$\sigma_1(p), \ldots, \sigma_k(p)$がファイバー$E_p$の基底となる(すなわち線形独立で$E_p$を張る)ものをいう.$U = M$のとき,大域枠(global frame)と呼ぶ.$E \to M$が滑らかなベクトル束である場合,すべての$\sigma_i$が滑らかな切断であるとき,その枠を滑らかな枠(smooth frame)という.枠$(\sigma_1, \ldots, \sigma_k)$は,しばしば$(\sigma_i)$のように表記する.
以前ベクトル場の稿で定義した$M$の(局所または大域)枠は,この新しい定義では接束の枠である.文脈に応じて両方の用語を使い分ける:「$M$の枠」と「$TM$の枠」は同じ意味である.
次の命題は,ベクトル場の稿で述べた命題のベクトル束版である:
局所枠の完備化
$E \to M$を階数$k$の滑らかなベクトル束とする.
- $U \subset M$上の滑らかな局所切断の$m$組$(\sigma_1, \ldots, \sigma_m)$が線形独立で,$1 \leq m < k$とする.このとき,任意の$p \in U$ に対して,$p$の近傍$V$と,$E$上の滑らかな切断$\sigma_{m+1}, \ldots, \sigma_k$が存在して,$(\sigma_1, \ldots, \sigma_k)$が$U \cap V$上の滑らかな局所枠となる.
- $p \in M$に対し,$E_p$の元$v_1, \ldots, v_m$が線形独立で,$1 \leq m \leq k$とする.このとき,$p$の近傍で定義された滑らかな局所枠$(\sigma_i)$が存在して,$\sigma_i(p) = v_i$($i=1,\ldots,m$)となる.
- $A \subset M$を閉集合とし,$E|_A$上の切断$(\tau_1, \ldots, \tau_k)$が線形独立かつ滑らかであるとする.このとき,$A$の近傍で定義された滑らかな局所枠$(\sigma_1, \ldots, \sigma_k)$が存在して,$\sigma_i|_A = \tau_i$($i=1,\ldots,k$)となる.
ベクトル束の局所枠は局所自明化と密接に関係しており,次の2つの例がそれを示している.
$E = M \times \mathbb{R}^k \to M$が直積束である場合,$\mathbb{R}^k$の基底$(e_1, \ldots, e_k)$から$E$の大域枠$(\tilde{e_i})$が得られる.ここで,$\tilde{e_i}(p) = (p, e_i)$で定める.$M$が(境界の有無を問わない)滑らかな多様体であれば,この大域枠は滑らかである.//
$E \to M$を滑らかなベクトル束とする.$\Phi: \pi^{-1}(U) \to U \times \mathbb{R}^k$が$E$の滑らかな局所自明化であるとき,前の例と同様の方法で$U$上の局所枠を構成できる.$U$上の写像$\sigma_1, \ldots, \sigma_k: U \to E$を $$ \sigma_i(p) = \Phi^{-1}(p, e_i)=\Phi^{-1}\circ\tilde{e}_i(p) $$ で定める: $$ \begin{CD} \pi^{-1}(U) @>{\Phi}>> U \times \mathbb{R}^k \\ @AA{\sigma_i}A @AA{\tilde{e}_i}A \\ U @= U \end{CD} $$ $\sigma_i$は$\Phi$が微分同相写像であるため滑らかであり,$\pi_1 \circ \sigma_i(p) = \pi \circ \Phi^{-1}(p, e_i) = \pi_1(p, e_i) = p$となるので,$\sigma_i$は切断である.また,$\Phi$は$E_p$から$\{p\} \times \mathbb{R}^k$への同型写像なので,$\sigma_i(p)$は$E_p$の基底となる.この局所枠$(\sigma_i)$を$\Phi$に対応する局所枠という.//
滑らかなベクトル束の任意の滑らかな局所枠は,上の例にあるような滑らかな局所自明化に対応する.
滑らかなベクトル束が滑らかに自明であることと,滑らかな大域枠を持つことは同値である.
この系を滑らかな多様体$M$の接束に適用すると,$TM$が自明束であることと,$M$が平行化可能であることは同値であることが分かる(以前,平行化可能多様体(parallelizable manifold)とはその接束に滑らかな大域枠を持つ多様体であると定義したことを思い出そう).
$E \to M$を階数$k$の滑らかなベクトル束とし,$(V, \varphi)$を$M$上の滑らかなチャート(座標関数は$x^i$)とする.$E$の$V$上に滑らかな局所枠$(\sigma_i)$が存在すると仮定する.写像$\tilde{\varphi}: \pi^{-1}(V) \to \varphi(V) \times \mathbb{R}^k$を $$ \tilde{\varphi}\left(v^i \sigma_i(p)\right) = (x^1(p), \ldots, x^n(p), v^1, \ldots, v^k) $$ で定めると,$(\pi^{-1}(V), \tilde{\varphi})$は$E$の滑らかな座標チャートとなる.
ベクトル場の滑らかさが任意の滑らかなチャートにおける成分関数によって特徴付けられるのと同様に,ベクトル束の切断の滑らかさも局所枠によって特徴付けられる.たとえば,$E$のある開集合$U \subset M$上に滑らかな局所枠 $(\sigma_i)$ が与えられているとする.$\tau: M \to E$が粗い切断であれば,任意の$p \in U$における$\tau$の値は,$\tau(p) = \tau^i(p)\sigma_i(p)$の形で一意的に表せる.このようにして定まる$k$個の関数$\tau^i: U \to \mathbb{R}$を,与えられた局所枠に関する$\tau$の成分関数(component functions)と呼ぶ.
局所枠による滑らかさの特徴付け
$E \to M$を滑らかなベクトル束とし,$\tau: M \to E$を粗い切断とする.$(\sigma_i)$が$E$の開集合$U \subset M$上の滑らかな局所枠であるとき,$\tau$が$U$上で滑らかであることと,その局所枠$(\sigma_i)$に関する成分関数が滑らかであることは同値である.
この命題は局所切断にも同様に適用できる.なぜなら,$E$の開部分集合$V \subset M$上の局所切断は,制限束$E|_V$の大域切断と同じ意味だからである.
局所枠と局所自明化の対応から,滑らかな多様体の接束の滑らかな構造を特徴付ける次の一意性の結果が導かれる.
接束の滑らかな構造の存在と一意性
$M$を(境界の有無を問わない)滑らかな$n$次元多様体とする.以前の命題で構成された$TM$上の位相と滑らかな構造は,次の条件を満たすものとして一意である:$\pi: TM \to M$が各ファイバーに与えられたベクトル空間構造のもとで滑らかなベクトル束となり,すべての座標ベクトル場が滑らかな局所切断となる.
束準同型
束準同型
$E \to M$および$E' \to M'$をベクトル束とする.連続写像$F: E \to E'$が,ある写像$f: M \to M'$に対して $$ \pi' \circ F = f \circ \pi $$ を満たす,すなわち図式 $$ \begin{CD} E @>F>> E' \\ @V\pi VV @V\pi'VV \\ M @>f>> M' \end{CD} $$ が可換なとき,$F$を束準同型(bundle homomorphism)という.
このとき,任意の$p \in M$について,$F$のファイバーへの制限$F|_{E_p}: E_p \to E'_{f(p)}$は線形写像である.この関係は「$F$は$f$を被覆する」と表現される.
$E \to M$および$E' \to M'$をベクトル束とし,$F: E \to E'$を$f: M \to M'$を被覆する束準同型とする.このとき,$f$は連続写像であり,$F$によって一意的に定まる.もし両方の束と$F$が滑らかであれば,$f$も滑らかである.
(滑らかな)束同型
全射な束準同型$F: E \to E'$ で,逆写像も束準同型であるものを束同型(bundle isomorphism)という.$F$がさらに微分同相写像である場合,滑らかな束同型(smooth bundle isomorphism)という.$E$と$E'$の間に(滑らかな)束同型が存在するとき,$E$と$E'$は(滑らかに)同型((smoothly) isomorphic)であるという.
特に$E$と$E'$の両方が同じ底空間$M$上のベクトル束である場合,より制限された「束準同型」の概念が有用となる.$M$上の束準同型とは,$M$の恒等写像を被覆する束準同型,すなわち$\pi' \circ F = \pi$を満たす,すなわち図式 $$ \begin{CD} E @>F>> E' \\ @V\pi VV @V\pi'VV \\ M @= M \end{CD} $$ が可換図式となる連続写像$F: E \to E'$のことであり,各ファイバーへの制限が線形写像となる. さらに,$M$上の(滑らかな)束同型$F: E \to E'$が存在するとき,$E$と$E'$は$M$上で(滑らかに)同型であるという.
次の命題は,逆写像の滑らかさを確認する必要がないことを示している:
$E$および$E'$を(境界の有無を問わない)滑らかな多様体$M$上の滑らかなベクトル束とし,$F: E \to E'$を$M$上の全単射な滑らかな束準同型とする.このとき,$F$は滑らかな束同型である.
$F: M \to N$が滑らかな写像であるならば,その全微分$dF: TM \to TN$は$F$を被覆する滑らかな束準同型である.//
$E \to M$および$E' \to M$を(境界の有無を問わない)滑らかな多様体$M$上の滑らかなベクトル束とし,$\Gamma(E)$, $\Gamma(E')$をそれぞれの滑らかな大域切断全体の空間とする.$F: E \to E'$が$M$上の滑らかな束準同型であるとき,$F$との合成によって$\Gamma(E) \to \Gamma(E')$への写像$\tilde{F}$が誘導される: $$ \tilde{F}(\sigma)(p) = (F \circ \sigma)(p) = F(\sigma(p)) $$ $\tilde{F}(\sigma)$は$E'$の切断であり,合成の滑らかさから滑らかであることは容易に分かる.
束準同型は各ファイバー上で線形であるため,誘導される切断上の写像$\tilde{F}$も$\mathbb{R}$上線形となる.実際には,さらに強い線形性の性質を満たす.
$C^{\infty}$上線形
写像 $$ \mathfrak{F}: \Gamma(E) \to \Gamma(E') $$ が$C^\infty(M)$ 上線形(linear over $C^\infty(M)$)であるとは,任意の滑らかな関数$u_1, u_2 \in C^\infty(M)$と滑らかな切断$\sigma_1, \sigma_2 \in \Gamma(E)$に対して $$ \mathfrak{F}(u_1 \sigma_1 + u_2 \sigma_2) = u_1 \mathfrak{F}(\sigma_1) + u_2 \mathfrak{F}(\sigma_2) $$ を満たすことをいう.
定義から,滑らかな束準同型が誘導する切断上の写像は$C^\infty(M)$上線形であることは容易に分かる.次の補題は,その逆も成り立つことを示している:
束準同型の特徴付け
$M$を(境界の有無を問わない)滑らかな多様体とし,$E \to M$,$E' \to M$を$M$上の滑らかなベクトル束とする.$\Gamma(E)$,$\Gamma(E')$をそれぞれの滑らかな大域切断全体の空間とする.写像$\mathfrak{F}: \Gamma(E) \to \Gamma(E')$が$C^\infty(M)$上線形であることと,$M$上の滑らかな束準同型$F: E \to E'$が存在して,任意の$\sigma \in \Gamma(E)$について$\mathfrak{F}(\sigma) = F \circ \sigma$となることは同値である.
後でさらに多くの道具を整えた後に,滑らかな束準同型の多くの例を見ていく.ここではまず,いくつかの基本的な例を示す.
$M$を滑らかな多様体とし,$f \in C^\infty(M)$とする.$\mathfrak{X}$から自身への写像$X \mapsto fX$は$C^\infty(M)$上線形である.実際,任意の$u_1,u_2 \in C^\infty(M)$とベクトル場$X_1,X_2$に対して $$ f(u_1X_1+u_2X_2)=u_1fX_1+u_2fX_2 $$ が成り立つ.したがってこれは$TM$から自身への滑らかな$M$上の束準同型を定める.//
$Z$を$\mathbb{R}^3$上の滑らかなベクトル場とすると,$Z$との外積により 写像$X \mapsto X \times Z$が$\mathfrak{X}$から自身への写像として定まる.この写像は$X$に関して$C^\infty(\mathbb{R}^3)$上線型であるため,$T\mathbb{R}^3$から$T\mathbb{R}^3$への$\mathbb{R}^3$上の滑らかな束準同型を定める.//
$Z$を$\mathbb{R}^n$上の滑らかなベクトル場とすると,Euclid内積により写像 $X \mapsto X\cdot Z$が切断空間$\mathfrak{X}(\mathbb{R}^n)$から$C^\infty(\mathbb{R}^n)$への写像として定まり,これは$C^\infty(\mathbb{R}^n)$上線形である.したがって,$T\mathbb{R}^n$から自明線束$\mathbb{R}^n \times \mathbb{R}$への滑らかな束準同型を定める.//
この補題のおかげで,通常は$\tilde{F}$という記法を省略し,$M$上の束準同型$F: E \to E'$と,それが切断上に誘導する線形写像$F: \Gamma(E) \to \Gamma(E')$の両方に同じ記号を使い,どちらの型の写像も「束準同型」と呼ぶことにしている.切断上の作用は,単に各点ごとに束準同型を適用するだけで得られるので,混乱は生じないはずである.実際,私たちはこれまでにも,特定の場合には同じことをしてきた.例えば,$a \in \mathbb{R}$のとき,$X \mapsto aX$という記法は,各接空間 $T_pM$のベクトルを$a$倍する操作と,ベクトル場全体を$a$倍する操作の両方を表すのに使われる.$a$倍写像は$TM$から自身への束準同型なので,どちらの意味でも曖昧さは生じない.
微分を含む多くの写像は,束準同型にはならないことに注意が必要である.例えば,$M$上の滑らかなベクトル場$X$に対し,Lie微分作用素$\mathcal{L}_X : \mathfrak{X}(M) \to \mathfrak{X}(M)$は,接束から自身への束準同型ではない.なぜなら,$C^\infty(M)$上線形ではないからである.経験則として,滑らかな切断から滑らかな切断への線形写像が各点ごとに作用する場合は束準同型である可能性が高いが,微分を含む場合はそうでないことが多い.
部分束
ベクトル束の部分束
$E \to M$をベクトル束とする.その部分束(subbundle)とは,$E$の部分空間$D$と,$D$から$M$への射影$\pi_D:D \to M$の組$(D, \pi_D)$であって,$D$は$E$の位相的部分空間であり,$\pi_D$は$\pi_E$の$D$への制限であり,さらに各$p \in M$について$D_p = D \cap E_p$が$E_p$の線形部分空間となり,そのベクトル空間構造は$E_p$から誘導されるものである.
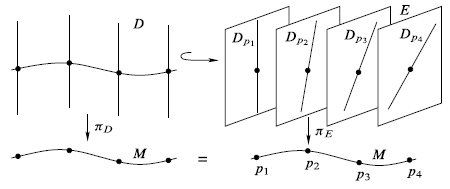
部分束$D$が$M$上のベクトル束となるためには,すべてのファイバー$D_p$が空でなく,かつ同じ次元を持つことが必要であることに注意する.
滑らかな部分束
$E \to M$が滑らかなベクトル束であるとき,その部分束$E$が滑らかな部分束(smooth subbundle)であるとは,$E$が滑らかなベクトル束であり,かつ$E$の部分多様体(境界の有無を問わない)として埋め込みになっている場合をいう.
次の補題は,部分空間の族$\{D_p \subset E_p \mid p \in M\}$の合併が滑らかな部分束となることを判定する便利な条件を与える:
部分束の局所枠による特徴付け
$E \to M$を滑らかなベクトル束とし,各$p \in M$に対して$E_p$の$m$次元線形部分空間$D_p \subset E_p$が与えられているとする.このとき,$D = \bigcup_{p \in M} D_p \subset E$が$E$の滑らかな部分束となるのは,次の条件が成り立つ場合に限る:
$M$の各点ごとに,その近傍$U$が存在して,$E$の滑らかな局所切断$\sigma_1, \ldots, \sigma_m: U \to E$があり,任意の$q \in U$で$\sigma_1(q), \ldots, \sigma_m(q)$が$D_q$の基底となる.
$M$を滑らかな多様体,$V$を$M$上のゼロ化されない(nowhere-vanishing)滑らかなベクトル場とする.各点$p\in M$におけるファイバーを$V_p$の線形結合とする集合$D \subset TM$は,$TM$の滑らかな階数$1$の部分束である.//
$E \to M$を任意の自明束とし,$(E_1,\ldots, E_k)$を$E$の滑らかな大域枠とする.$0 \leq m \leq k$のとき,各$p \in M$に対して$D_p = \mathrm{span}\{E_1|_p, \ldots, E_m|_p\}$ と定めることで得られる部分集合$D \subset E$は,$E$の滑らかな部分束である.//
(定)階数
$E \to M$および$E' \to M$をベクトル束とし,$F: E \to E'$を$M$上の束準同型とする.各 $p \in M$に対して,線形写像$F|_{E_p}$の階数を$F$の$p$における階数(rank)という.すべての$p \in M$で階数が一定であるとき,$F$は定階数(constant rank)であるという.
次の定理は,さらに多くの部分束を得る方法を示している:
$E \to M$,$E' \to M$を滑らかな多様体$M$上の滑らかなベクトル束とし,$F: E \to E'$を$M$上の滑らかな束準同型とする.各$p \in M$に対し,部分空間 $$ \mathrm{Ker} F = \bigcup_{p \in M} \mathrm{Ker} F|_{E_p}, \quad \mathrm{Im} F = \bigcup_{p \in M} \mathrm{Im} F|_{E_p} $$ を定める.このとき,$\mathrm{Ker} F$および$\mathrm{Im} F$がそれぞれ$E$,$E'$の滑らかな部分束となるのは,$F$が定階数である場合に限る.
次の命題は,$\mathbb{R}^n$の部分多様体上の接束の興味深い部分束を構成する別の方法を示している:
直交補束
$M$を$\mathbb{R}^n$の(境界の有無を問わない)埋め込み部分多様体とし,$D$を$T\mathbb{R}^n|_M$の滑らかな階数$k$の部分束とする.各$p \in M$に対し,$D_p^\perp$をEuclid内積に関する$T_p\mathbb{R}^n$内の$D_p$の直交補空間とし,$D^\perp \subset T\mathbb{R}^n|_M$を $$ D^{\perp} = \{ (p, v) \in T\mathbb{R}^n \mid p \in M,\, v \in D_p^{\perp} \} $$ で定める.このとき,$D^\perp$は$T\mathbb{R}^n|_M$の滑らかな階数$n-k$の部分束となる.また,各$p \in M$の近傍で,$D^\perp$の滑らかな正規直交枠が存在する.
部分多様体の法線束
$M$を$\mathbb{R}^n$の(境界の有無を問わない)$m$次元埋め込み部分多様体とする.このとき,その法線束$NM$は$T\mathbb{R}^n|_M$の滑らかな階数$n-m$の部分束となる.各$p \in M$の近傍で,$NM$の滑らかな正規直交枠が存在する.
ファイバー束
最後に,ベクトル束の重要な一般化について簡単に紹介する.ここではファイバーがベクトル空間ではなく任意の位相空間であるような「ファイバー束」を考える.ここでは定義に触れるだけにとどめるが,ファイバー束は多様体論の多くの応用で現れるため,少なくともその定義には慣れておくことが重要である.
ファイバー束
$M$および$F$を位相空間とする.$M$上のファイバー束(fiber bundle)とは,位相空間$E$と,$E$から$M$への全射連続写像$\pi: E \to M$の組で,次の性質を満たすものである:任意の$x \in M$に対し,$x$の近傍$U \subset M$と,$\pi^{-1}(U)$から$U \times F$への同相写像$\Phi: \pi^{-1}(U) \to U \times F$($E$の$U$上の局所自明化(local trivialization)と呼ぶ)が存在し,次の図式が可換となる: $$ \begin{CD} \pi^{-1}(U) @>\Phi>> U \times F \\ @V\pi VV @VV\pi_1 V \\ U @= U \end{CD} $$ ここで,$\pi_1: U \times F \to U$ は射影写像である.$E, M, F$が(境界の有無を問わない)滑らかな多様体で,$\pi$が滑らかな写像,局所自明化が微分同相写像として選べる場合,滑らかなファイバー束(smooth fiber bundle)という.
ファイバー束の定義に関して,
- 位相空間$E$を全空間(total space)という.
- 位相空間$M$を底空間(base space)という.
- 写像$\pi$を射影(projection)という.
自明ファイバー束
自明ファイバー束(trivial fiber bundle)とは,底空間全体にわたる局所自明化(大域自明化(global trivialization)という)を持つファイバー束のことである.滑らかなファイバー束が大域自明化を持ち,その自明化が微分同相写像である場合,そのファイバー束は滑らかに自明(smoothly trivial)であるという.
任意の積空間$M \times F$は射影$\pi_1: M \times F \to M$をもつファイバー束であり,これを直積ファイバー束(product fiber bundle)と呼ぶ.恒等写像$\mathrm{Id}: M \times F \to M \times F$が大域自明化を与えるため,直積束は自明束である.//
任意の階数$k$のベクトル束は,ファイバーが$\mathbb{R}^k$であるファイバー束である.//
もし$E \to \mathbb{S}^1$がMöbius束であれば,商写像$q:\mathbb{R}^2 \to E$による$\mathbb{R}\times[-1,1]$の像は,ファイバー$[-1,1]$を持つ$S^1$上のファイバー束となる.これは自明束ではない.//
任意の被覆写像$\pi: E \to M$は,ファイバーが離散集合であるファイバー束である.局所自明化を構成するには,まず各ファイバーと同じ濃度を持つ離散空間$S$を取る.$M$の任意の同じ濃度で被覆される開集合$U \subset M$に対して,$\pi^{-1}(U)$の連結成分全体と$S$との間の全単射を選び,写像$\Phi: \pi^{-1}(U) \to U \times S$を次のように定める:各点$x\in\pi^{-1}(U)$について $\Phi(x)=(\pi(x),c(x))$とする.ここで$c(x)$は$x$を含む成分に対応する$S$の元である.//