接ベクトル
本稿は主に Lee の教科書 [Lee02] に基づいている.また日本語の文献として主に[松本88,中原18]を参考にしている.
微分の中心的な考え方は「線形近似」である.例えば,1変数関数はその接線で近似でき,$\mathbb{R}^n$内のパラメータ付き曲線はその速度ベクトルで近似でき,$\mathbb{R}^3$内の曲面はその接平面で近似でき,$\mathbb{R}^n$から$\mathbb{R}^m$への写像はその全微分で近似できる.
多様体上で微分を考えるためには,各点における多様体の「線形近似」として接空間を導入する必要がある.滑らかな多様体の定義が抽象的であるため,この接空間の定義には少し工夫が必要となる.
目次
接ベクトル
幾何的接ベクトル
まずはより具体的な対象,すなわち$\mathbb{R}^n$における幾何的な接ベクトルを考える.
幾何的接ベクトル
点$a \in \mathbb{R}^n$が与えられたとき,$\mathbb{R}^n$の$a$における幾何的接空間(geometric tangent space)$\mathbb{R}^n_a$とは,$\{a\}\times\mathbb{R}^n=\{(a, v) \mid v \in \mathbb{R}^n\}$である.$\mathbb{R}^n$における幾何的接ベクトル(geometric tangent vector)とは,ある$a \in \mathbb{R}^n$に対する$\mathbb{R}^n_a$の元である.
幾何的接ベクトル$(a, v)$を$v_a$(または,より明確にしたい場合は$v|_a$)と略記する.
$v_a$は,ベクトル$v$の始点が$a$にあるものと考える.
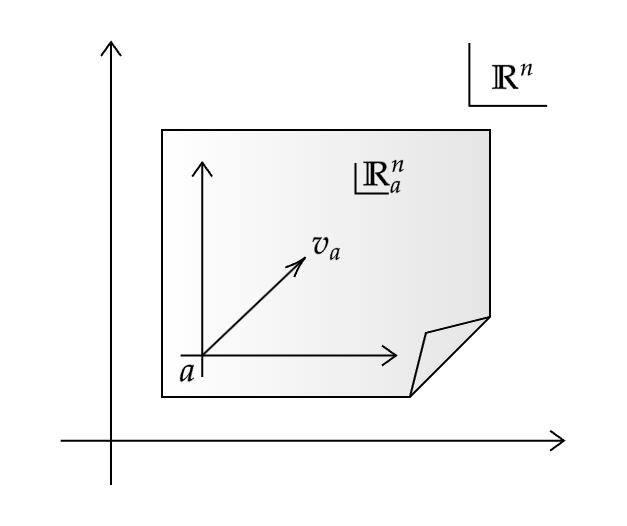
幾何的接空間$\mathbb{R}^n_a$は,自然な演算 $$ v_a + w_a \equiv (v + w)_a,\quad c(v_a) \equiv (cv)_a $$ によって実ベクトル空間となる.
ベクトル空間としては$\mathbb{R}^n_a$は$\mathbb{R}^n$そのものと本質的に同じであり,添字 $a$を付ける理由は,異なる点$a$と$b$における幾何的接空間$\mathbb{R}^n_a$と$\mathbb{R}^n_b$が互いに素な集合となるようにするためである.
この定義を用いると,$S^{n-1}$ のある点$a \in S^{n-1}$における接空間は,$\mathbb{R}^n_a$ の中で,$a$を通り,動径方向の単位ベクトルと直交するベクトル全体の部分空間として考えることができる.ここで,$\mathbb{R}^n_a$の内積は自然な同型$\mathbb{R}^n \cong \mathbb{R}^n_a$を通じて$\mathbb{R}^n$から受け継がれる.
しかし,この定義には問題がある.それは,一般の滑らかな多様体上で接ベクトルをどのように定義すればよいかの手がかりを与えてくれないことである.なぜなら,一般の多様体には周囲を囲むEuclid空間が存在しないからである.したがって,多様体上でも意味を持つような,別の接ベクトルの特徴付けを探す必要がある.
それは幾何的接ベクトルが関数の「方向微分」を与えるという特徴付けである:
任意の幾何的接ベクトル$v_a \in \mathbb{R}^n_a$は,方向$v$での$a$における方向微分作用素$D_v|_a : C^{\infty}(\mathbb{R}^n) \to \mathbb{R}$を次のように定める: $$ D_v|_a f = D_v f(a) = \frac{d}{dt}\bigg|_{t=0} f(a + t v) $$ この作用は$\mathbb{R}$上線形であり,Leibniz則を満たす: $$ D_v|_a(fg) = f(a) D_v|_a g + g(a) D_v|_a f $$ $\mathbb{R}^n_a$の基底を$e_i|_a$($i=1,\ldots,n$)で表し,$v_a=v^ie_i|_a$と表すと,連鎖律より,より具体的に $$ D_v|_a f = v^i \frac{\partial f}{\partial x^i}(a) $$ と表せる(Einsteinの和の規約を用いた).//
この構成を念頭に,一般に次のように定義する:
微分作用素
$a$を$\mathbb{R}^n$の点とする.写像$w:C^{\infty}(\mathbb{R}^n)\to\mathbb{R}$が,$\mathbb{R}^n$の$a$における微分作用素(derivation)であるとは,$w$が$\mathbb{R}$上線形であり,Leibniz則 $$ w(fg) = f(a) w(g) + g(a) w(f) $$ を満たすことをいう.$C^{\infty}(\mathbb{R}^n)$の$a$における微分作用素全体の集合を $T_a\mathbb{R}^n$と表す.
$T_a\mathbb{R}^n$は次の演算でベクトル空間となる: $$ (w_1 + w_2)(f) \equiv w_1(f) + w_2(f), \quad (cw)(f) \equiv c(wf) $$
微分作用素$w$の性質として以下のものがある:
- $f$が定数関数ならば,$w(f) = 0$である.
- $f(a) = g(a) = 0$ならば,$w(fg) = 0$である.
$T_a\mathbb{R}^n$について最も重要な事実は,$T_a\mathbb{R}^n$が$\mathbb{R}_a^n$と自然に同型になることである:
$a \in \mathbb{R}^n$とする.
- 各幾何的接ベクトル$v_a \in \mathbb{R}^n_a$に対し,方向微分作用素$D_v|_a : C^\infty(\mathbb{R}^n) \to \mathbb{R}$は,$a$における微分作用素である.
- 写像$v_a \mapsto D_v|_a$は,$\mathbb{R}^n_a$から$T_a\mathbb{R}^n$への同型写像である.
任意の$a \in \mathbb{R}^n$に対して,$n$個の微分作用素 $$ \frac{\partial}{\partial x^1}\bigg|_a, \ldots, \frac{\partial}{\partial x^n}\bigg|_a\quad\text{defined by}\quad \frac{\partial}{\partial x^i}\bigg|_a f = \frac{\partial f}{\partial x^i}(a) $$ は$T_a\mathbb{R}^n$の基底をなす.したがって,$T_a\mathbb{R}^n$の次元は$n$である.
多様体上の接ベクトル
これで,多様体および境界付き多様体上の接空間を定義する準備が整った.これまでの概念を一般化する:
接空間
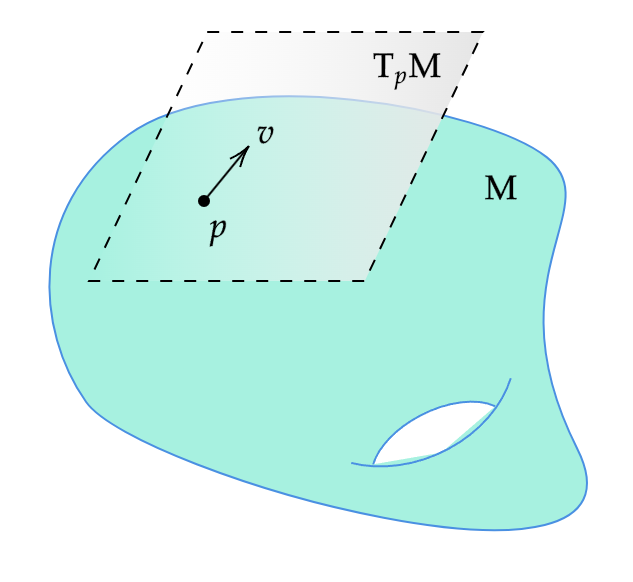
$M$を(境界の有無を問わない)滑らかな多様体,$p$を$M$の点とする.線形写像$v:C^{\infty}(M)\to\mathbb{R}$が,すべての$f, g \in C^\infty(M)$に対して $$ v(fg) = f(p) v(g) + g(p) v(f) $$ を満たすとき,$v$を$p$における微分作用素(derivation)という.
$p$におけるすべての微分作用素の集合を$M$の$p$における接空間(tangent space)といい$T_pM$と表す.$T_p M$の元を$p$における接ベクトル(tangent vector)と呼ぶ.
接ベクトルの性質は,以前述べた微分作用素の性質と同じである:$M$を(境界の有無を問わない)滑らかな多様体,$p \in M$,$v \in T_p M$,$f, g \in C^\infty(M)$とする.
- $f$が定数関数ならば,$v(f) = 0$である.
- $f(p) = g(p) = 0$ならば,$v(fg) = 0$である.
$\mathbb{R}^n$における幾何的接ベクトルを念頭に置くと,多様体$M$上の接ベクトルも「$M$に接する矢印」であり,その根元が$M$の各点に付随しているものとして視覚化するとよい(接ベクトルに関する定理の証明は,もちろん微分作用素による抽象的な定義に基づいて行う必要がある).
滑らかな写像の微分
多様体上の抽象的な接空間と,$\mathbb{R}^n$における幾何的な接空間を結びつけるためには,滑らかな写像が接ベクトルにどのような影響を与えるかを考える必要がある.Euclid空間間の滑らかな写像の場合,その点における全微分(Jacobi行列で表される)は,その点付近で写像を最もよく近似する線形写像を与える.多様体の場合も同様に線形写像が存在するが,多様体間の線形写像というものは意味をなさない.そこで,接空間同士の間の線形写像として定式化することになる.
微分
$M, N$を(境界の有無を問わない)滑らかな多様体とし,$F: M \to N$を滑らかな写像とする.各$p \in M$に対して,写像 $$ dF_p: T_p M \to T_{F(p)} N $$ を$F$の$p$における微分(differential)と呼び,次のように定義する:$v \in T_p M$に対し,$dF_p(v)$は$F(p)$における微分作用素であり,$f \in C^\infty(N)$ に対して $$ dF_p(v)(f) = v(f \circ F) $$ となる(下図参照).
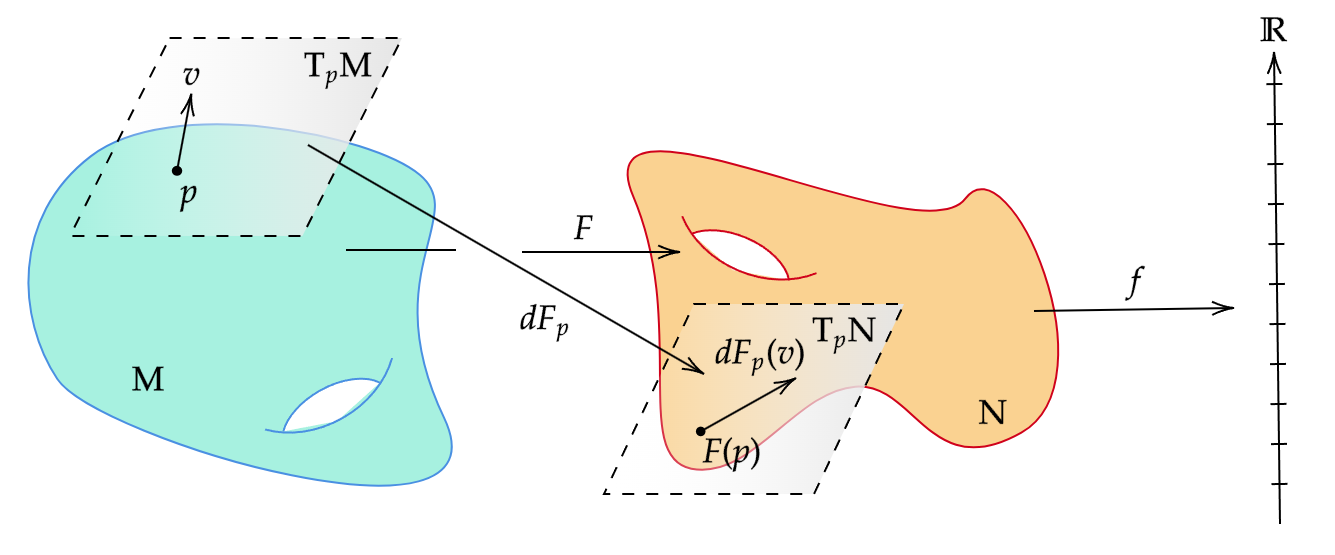
$f \in C^\infty(N)$ならば$f \circ F \in C^\infty(M)$なので,$v(f \circ F)$は意味を持つ.演算子$dF_p(v): C^\infty(N) \to \mathbb{R}$は,$v$が線形性より線形写像であり,また$F(p)$における微分作用素となる.つまり,行き先が微分作用素となるような接空間の間の写像が微分である.
微分の性質として以下のものがある:$M, N, P$を(境界の有無を問わない)滑らかな多様体とし,$F: M \to N$,$G: N \to P$を滑らかな写像,$p \in M$とする.
- $dF_p: T_p M \to T_{F(p)} N$は線形写像である.
- $d(G \circ F)_p = dG_{F(p)} \circ dF_p : T_p M \to T_{G \circ F(p)} P$である.
- $d(\mathrm{Id}_M)_p = \mathrm{Id}_{T_p M} : T_p M \to T_p M$である.
- $F$が微分同相写像ならば,$dF_p: T_p M \to T_{F(p)} N$は同型写像であり,その逆写像は$(dF_p)^{-1} = d(F^{-1})_{F(p)}$である.
微分の最初の重要な応用は,座標チャートを用いて多様体上のある点の接空間とEuclid空間の接空間を対応させることである.しかし,ここで重要な技術的問題がある:接空間は多様体全体上の滑らかな関数によって定義されるが,座標チャートは一般に開集合上でしか定義されていない.問題を解決する鍵は次の命題で述べるように,接ベクトルの作用は局所的であるという点である:
$M$を(境界の有無を問わない)滑らかな多様体,$p \in M$,$v \in T_p M$とする.$f, g \in C^\infty(M)$が$p$のある近傍で一致するならば,$vf = vg$である.
この命題を用いることで,開部分多様体上の接空間と元の多様体全体の接空間を同一視できる:
$M$を(境界の有無を問わない)滑らかな多様体,$U \subset M$を開部分集合,$\iota: U \hookrightarrow M$を包含写像とする.任意の$p \in U$に対して,微分$d\iota_p: T_p U \to T_p M$は同型写像である.
開集合$U \subset M$が与えられたとき,$T_p U$と$T_p M$の間の同型写像$d\iota_p$は,いかなる選択にも依存せず自然に定まる.そこで今後は,任意の点$p \in U$に対して$T_p U$と$T_p M$を同一視することにする.
接空間の次元
$M$が$n$次元滑らかな多様体であるとき,各点$p \in M$における接空間$T_p M$は$n$次元ベクトル空間である.
次に,境界付き多様体についても同様の結果を証明する必要がある.実際,$M$が$n$次元境界付き多様体であるとき,$M$の境界点における接空間がどのようなものになるべきかは,直感的にはすぐには明らかでない.内部点と同様に$n$次元ベクトル空間になるべきなのか,それとも境界と同じく$(n-1)$次元になるべきなのか,あるいは$M$が局所的にモデル化されている半空間$\mathbb{H}^n$のような$n$次元の半空間になるべきなのか,という疑問が生じる.
しかし,以下で示すように,我々の定義から境界点における接空間も内部点と同様に$n$次元ベクトル空間になることが分かる.この選択が幾何的に最も直感的かどうかは場合によるが,境界付き多様体上の幾何的対象の定義が,通常の多様体の場合とほとんど同じ形になるという利点がある.
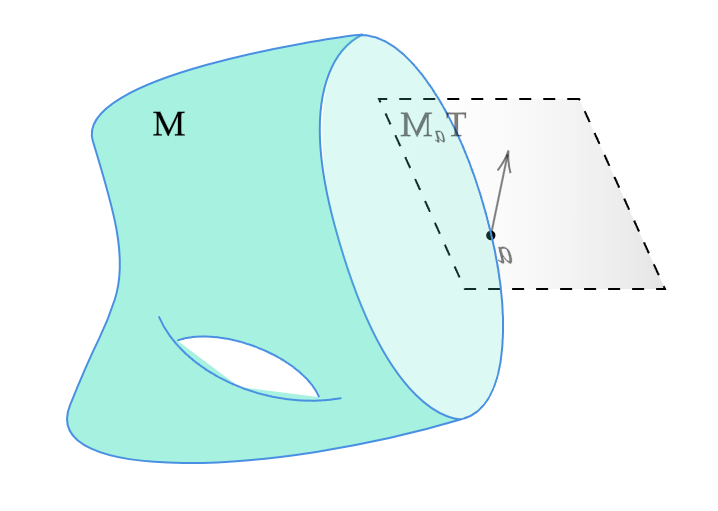
まず,$a \in \partial\mathbb{H}^n$ のとき,$\mathbb{H}^n$における接空間$T_a \mathbb{H}^n$と$\mathbb{R}^n$における接空間$T_a \mathbb{R}^n$の関係を明らかにする必要がある.
包含写像$\iota: \mathbb{H}^n \hookrightarrow \mathbb{R}^n$を考える.任意の$a \in \partial \mathbb{H}^n$に対して,微分$d\iota_a: T_a \mathbb{H}^n \to T_a \mathbb{R}^n$は同型写像である.
$U$が$M$の開部分集合であるとき$T_p U$と$T_p M$を同一視したのと同様に,この補題を用いて$a \in \partial\mathbb{H}^n$のとき$T_a \mathbb{H}^n$と$T_a \mathbb{R}^n$を同一視する.
境界付き多様体の接空間の次元
$M$を$n$次元境界付き滑らかな多様体とする.各点$p \in M$における接空間$T_p M$は$n$次元ベクトル空間である.
任意の有限次元ベクトル空間は,基底やノルムの選び方に依存しない自然な滑らかな多様体構造を持つ.次の命題は,ベクトル空間の接空間が自然にそのベクトル空間自身と同一視できることを示している:
準備として,$V$を有限次元ベクトル空間,$a \in V$とする.$\mathbb{R}^n$の場合と同様に,任意のベクトル$v \in V$に対して,写像$D_v|_a : C^\infty(V) \to \mathbb{R}$を $$ D_v|_a f = \frac{d}{dt}\bigg|_{t=0} f(a + t v) $$ により定める.
$V$を有限次元ベクトル空間とし,その自然な滑らかな多様体構造を考える.各点$a \in V$に対して,写像$v \mapsto D_v|_a$は,$V$から$T_a V$への自然な同型写像となる.また,任意の線形写像$L: V \to W$に対して,次の図式が可換となる: $$ \begin{CD} V @>{\cong}>> T_a V \\ @V{L}VV @VV{dL_a}V \\ W @>>{\cong}> T_{L(a)} W \end{CD} $$
各同型写像$V \cong T_a V$は,基底の選び方に依存せず自然に定まることに注意する.この結果により,有限次元ベクトル空間の接ベクトルは,その空間自身の元と同一視してよい.より一般に,$M$がベクトル空間$V$の開部分多様体である場合,$T_p M \leftrightarrow T_p V \leftrightarrow V$ という同型を組み合わせて,$M$の各点における接空間を$V$と自然に同一視できる.
例えば,$\mathrm{GL}(n, \mathbb{R})$はベクトル空間$M(n, \mathbb{R})$の開部分多様体なので,$\mathrm{GL}(n, \mathbb{R})$の各点$X$における接空間は$M(n, \mathbb{R})$と同一視できる(cf.Lie群とLie代数).//
積多様体の接空間については,もう一つ自然な同一視が存在する:
$M_1, \ldots, M_k$を滑らかな多様体とし,各$j$について$\pi_j: M_1 \times \cdots \times M_k \to M_j$を$M_j$成分への射影とする.任意の点$p = (p_1, \ldots, p_k) \in M_1 \times \cdots \times M_k$に対して, $$ \alpha: T_p(M_1 \times \cdots \times M_k) \to T_{p_1}M_1 \oplus \cdots \oplus T_{p_k}M_k $$ を $$ \alpha(v) = (d(\pi_1)_p(v), \ldots, d(\pi_k)_p(v)) $$ で定めると,$\alpha$は同型写像となる.同様のことは,$M_i$のうち1つが境界付き滑らかな多様体である場合にも成り立つ.
何度も強調しているが,この同型写像は座標の選び方に依存せず自然に定まるので,これを自然な同一視とみなすことができ,今後も常にそうすることにする.例えば,$T_{(p,q)}(M \times N)$を $T_p M \oplus T_q N$と同一視し,$T_p M$や$T_q N$を$T_{(p,q)}(M \times N)$の部分空間として扱える.
座標系における計算
ここまでの多様体の接空間の定義は非常に抽象的である.より具体的に理解するために,局所座標系において接ベクトルや微分の計算をどのように行うかを説明する.
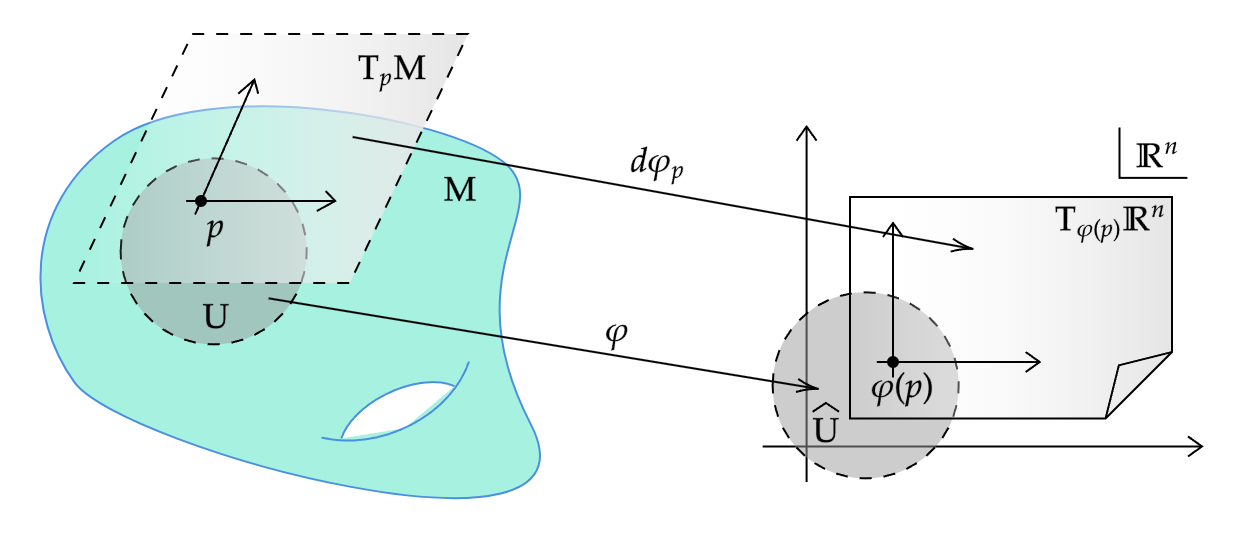
まず,$M$が滑らかな多様体であり,$(U, \varphi)$が$M$上の滑らかなチャートであるとする.このとき,$\varphi$は特に$U$から$\mathbb{R}^n$の開部分集合$\hat{U}$への微分同相写像である.以前示した命題から,$d\varphi_p: T_p M \to T_{\varphi(p)} \mathbb{R}^n$は同型写像である.
微分作用素$\frac{\partial}{\partial x^1}\big|_{\varphi(p)}, \ldots, \frac{\partial}{\partial x^n}\big|_{\varphi(p)}$は$T_{\varphi(p)}\mathbb{R}^n$の基底をなす.したがって,この同型写像$d\varphi_p$の逆像は$T_p M$の基底を与える.標準的な慣習に従い,座標写像による同一視が可能な場合には,これらのベクトルを$\frac{\partial}{\partial x^i}\big|_p$と表記する.このベクトルは,次の式で特徴付けられる: $$ \frac{\partial}{\partial x^i}\bigg|_p=(d\varphi_p)^{-1}\left(\frac{\partial}{\partial x^i}\bigg|_{\varphi(p)}\right)=d(\varphi^{-1})_{\varphi(p)}\left(\frac{\partial}{\partial x^i}\bigg|_{\varphi(p)}\right) $$ 微分の定義より,$\frac{\partial}{\partial x^i}\big|_p$は関数$f \in C^\infty(U)$に対して次のように作用する: $$ \frac{\partial}{\partial x^i}\bigg|_p f = \frac{\partial}{\partial x^i}\bigg|_{\varphi(p)} (f \circ \varphi^{-1}) = \frac{\partial \hat{f}}{\partial x^i}(\hat{p}) $$ ここで,$\hat{f} = f \circ \varphi^{-1}$は$f$の座標表示,$\hat{p}=(p^1,\ldots,p^n) = \varphi(p)$は$p$の座標表示である.言い換えると,「$\frac{\partial}{\partial x^i}\big|_p$は,$f$の座標表示の$i$番目の偏微分を$p$の座標で評価する微分作用素」である.これらのベクトル$\frac{\partial}{\partial x^i}\big|_p$を,その座標系に関する$p$での座標ベクトルと呼ぶ.
$M$が境界付き滑らかな多様体で,$p$がその内部点である場合,これまでの議論はそのまま適用できる.一方で$p \in \partial M$の場合,唯一必要な変更は$\mathbb{R}^n$を$\mathbb{H}^n$に置き換えることであり,記法$\frac{\partial}{\partial x^i}\big|_p$は$T_{\varphi(p)} \mathbb{R}^n$の元としても$T_{\varphi(p)} \mathbb{H}^n$ の元としても同じように用いることができる(これは先の$d\iota_{\varphi(p)}: T_{\varphi(p)} \mathbb{H}^n \to T_{\varphi(p)} \mathbb{R}^n$による同一視の結果である).特に$n$番目の座標ベクトル$\frac{\partial}{\partial x^n}\big|_p$は,この場合「片側微分」として解釈される.
以上の議論をまとめると,次の命題が得られる:
$M$を(境界の有無を問わない)滑らかな$n$次元多様体,$p \in M$とする.このとき$T_p M$は$n$次元のベクトル空間であり,$p$を含む任意の滑らかなチャート$(U, (x^i))$に対して,座標ベクトル $$ \frac{\partial}{\partial x^1}\bigg|_p, \ldots, \frac{\partial}{\partial x^n}\bigg|_p $$ は$T_p M$の基底をなす.
したがって,任意の接ベクトル$v \in T_p M$は,座標ベクトルの線形結合として一意的に $$ v = v^i \frac{\partial}{\partial x^i}\bigg|_p $$ と表せる.
座標基底
順序付き基底$\left( \frac{\partial}{\partial x^i}\big|_p \right)$を$T_p M$の座標基底(coordinate basis)と呼び,$v^1, \ldots, v^n$をその座標基底に関する$v$の成分(component)という.
$v$が与えられたとき,その成分は座標関数への作用から簡単に計算できる(ここで$x^j$は$U$上の滑らかな実数値関数とみなす): $$ v(x^j) = \left( v^i \frac{\partial}{\partial x^i}\bigg|_p \right)(x^j) = v^i \frac{\partial x^j}{\partial x^i}(p) = v^j $$
座標系における微分
次に,座標系における微分がどのように表されるかを考える.まず,特別な場合を考える:$U \subset \mathbb{R}^n$および$V \subset \mathbb{R}^m$をEuclid空間の開集合とし,$F: U \to V$を滑らかな写像とする.任意の$p \in U$に対して,$dF_p: T_p\mathbb{R}^n \to T_{F(p)}\mathbb{R}^m$の座標基底による行列表現を求める.定義域の座標を$(x^1, \ldots, x^n)$,値域の座標を$(y^1, \ldots, y^m)$とすると,連鎖律を用いて$dF_p$が基底ベクトルに作用は次のように計算できる: \begin{align} dF_p\bigg( \frac{\partial}{\partial x^i}\bigg|_p \bigg)f=&\frac{\partial}{\partial x^i}\bigg|_p(f\circ F)=\frac{\partial f}{\partial y^j}(F(p))\frac{\partial F^j}{\partial x^i}(p) \\ =& \bigg( \frac{\partial F^j}{\partial x^i}(p)\frac{\partial}{\partial y^j}\bigg|_{F(p)} \bigg)f \end{align} よって, $$ dF_p\left( \frac{\partial}{\partial x^i}\bigg|_p \right)=\frac{\partial F^j}{\partial x^i}(p)\frac{\partial}{\partial y^j}\bigg|_{F(p)} $$ つまり,$dF_p$の座標基底による行列は $$ \begin{pmatrix} \frac{\partial F^1}{\partial x^1}(p) & \cdots & \frac{\partial F^1}{\partial x^n}(p) \\ \vdots & \ddots & \vdots \\ \frac{\partial F^m}{\partial x^1}(p) & \cdots & \frac{\partial F^m}{\partial x^n}(p) \end{pmatrix} $$ となる(この行列の各列は,基底ベクトルの像の成分である).この行列は,$F$の$p$におけるJacobi行列であり,全微分$DF_p: \mathbb{R}^n \to \mathbb{R}^m$の行列表現そのものである.したがって,この場合,$dF_p: T_p\mathbb{R}^n \to T_{F(p)}\mathbb{R}^m$は,Euclid空間とその接空間の同一視のもとで,全微分$DF_p: \mathbb{R}^n \to \mathbb{R}^m$に対応する.同様の計算は,$U$が$\mathbb{H}^n$の開部分集合,$V$が$\mathbb{H}^m$の開部分集合の場合にも成り立つ.
次に一般的な状況を考える:(境界の有無を問わない)滑らかな多様体$M, N$間の滑らかな写像$F: M \to N$を考える.$p \in M$の近傍で$M$の滑らかなチャート$(U, \varphi)$,$F(p)$の近傍で$N$の滑らかなチャート$(V, \psi)$を選ぶと,$F$の座標表示$\hat{F} = \psi \circ F \circ \varphi^{-1} : \varphi(U \cap F^{-1}(V)) \to \psi(V)$が得られる.$y_p = \varphi(p)$を$p$の座標表示とする.$F \circ \varphi^{-1} = \psi^{-1} \circ \hat{F}$ であることを使うと, \begin{align} dF_p\bigg(\frac{\partial}{\partial x^i}\bigg|_p\bigg) =&\ dF_p\bigg( d(\varphi^{-1})_{\hat{p}}\bigg( \frac{\partial}{\partial x^i}\bigg|_{\hat{p}} \bigg) \bigg) \\ =&\ d(\psi^{-1})_{\hat{F}(\hat{p})}\bigg( d\hat{F}_{\hat{p}}\bigg( \frac{\partial}{\partial x^i}\bigg|_{\hat{p}} \bigg) \bigg) \\ =&\ d(\psi^{-1})_{\hat{F}(\hat{p})}\bigg( \frac{\partial\hat{F}^j}{\partial x^i}(\hat{p})\frac{\partial}{\partial y^j}\bigg|_{\hat{F}(\hat{p})} \bigg) \\ =&\ \frac{\partial\hat{F}^j}{\partial x^i}(\hat{p})\frac{\partial}{\partial y^j}\bigg|_{F(p)} \end{align} したがって,$dF_p$は座標基底に関して$F$の座標表示$\hat{F}$のJacobi行列で表される.
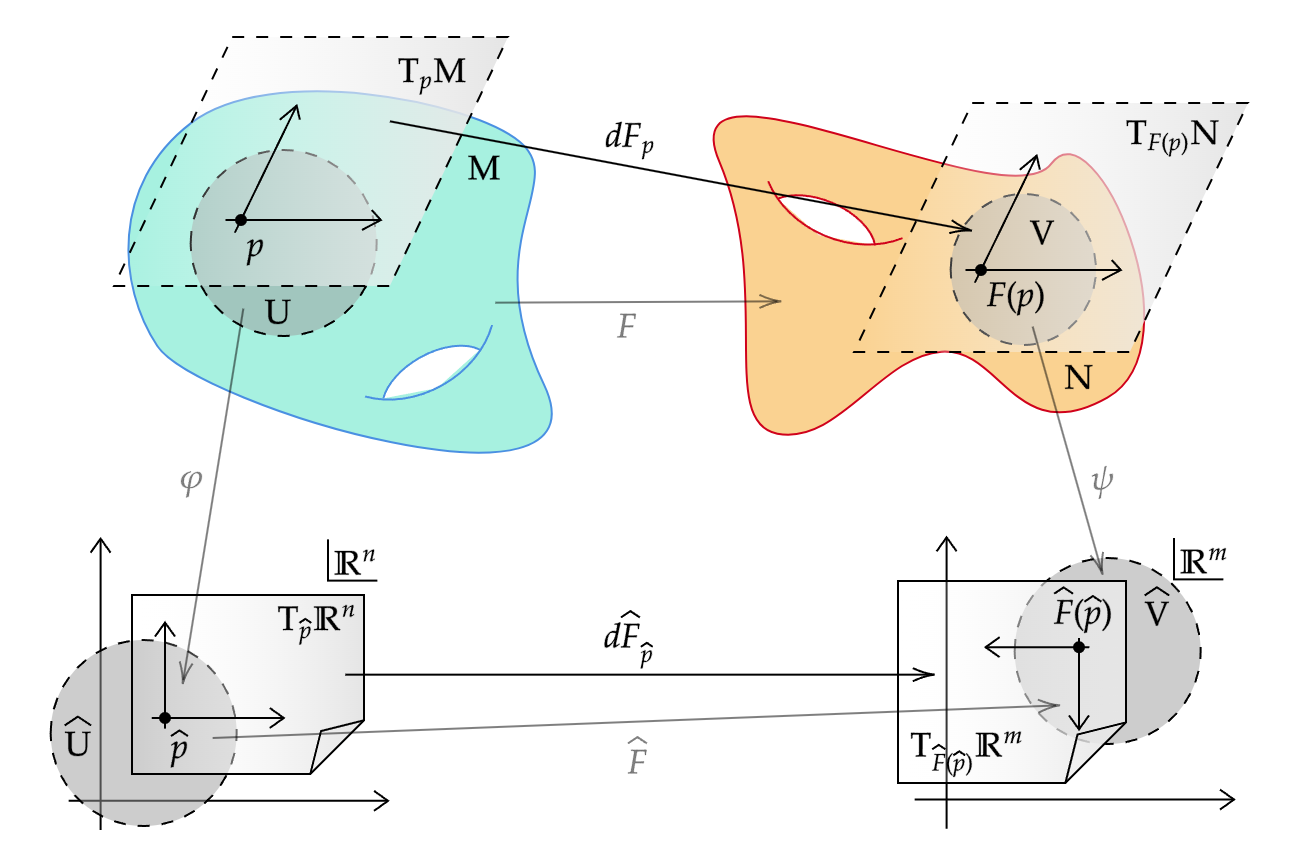
微分幾何学の文献では,「微分(differential)」は「接写像(tangent map)」「全微分(total derivative)」,あるいは単に「$F$の微分(derivative)」などと呼ばれることがある.また,接ベクトルを定義域の多様体から値域の多様体へ「push」することから,「pushforward」とも呼ばれる.文献によっては微分を $$ F'(p),\quad DF,\quad DF(p),\quad F_*,\quad TF,\quad T_pF $$ など様々な記号で表す.ここでは多様体間の滑らかな写像の微分には$dF_p$という記法を用い,有限次元ベクトル空間間の写像の全微分には$DF(p)$を用いる.Euclid空間の場合,これは$F$のJacobi行列である.
座標変換
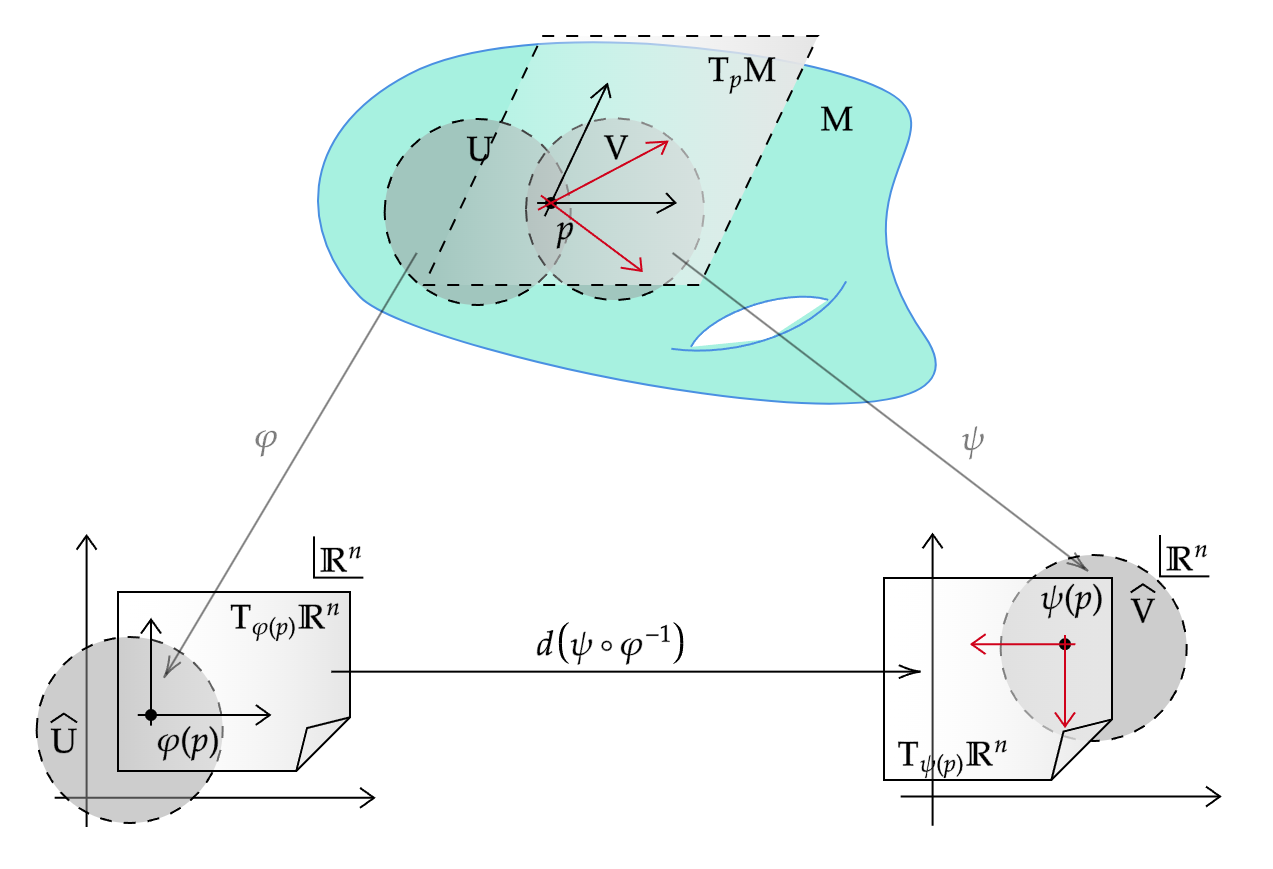
$M$上に2つの滑らかなチャート$(U, \varphi)$と$(V, \psi)$があり,$p \in U \cap V$とする.$\varphi$の座標関数を$(x^i)$,$\psi$の座標関数を$(\tilde{x}^i)$と表す.任意の接ベクトルは,$p$において基底$\left( \frac{\partial}{\partial x^i}\big|_p \right)$でも$\left( \frac{\partial}{\partial \tilde{x}^i}\big|_p \right)$でも表現できる.この2つの表現はどのような関係になるだろうか?
この状況では,変換写像$\psi \circ \varphi^{-1} : \varphi(U \cap V) \to \psi(U \cap V)$を次のような略記で表すのが便利である: $$ \psi\circ\varphi^{-1}(x)=(\tilde{x}^1(x), \ldots, \tilde{x}^n(x)) $$ ここで,$\tilde{x}^i(x)$という表記は典型的な記法の濫用であることに注意する.微分$d(\psi \circ \varphi^{-1})_{\varphi(p)}$は次のように書ける: $$ d(\psi\circ\varphi^{-1})_{\varphi(p)}\left( \frac{\partial}{\partial x^i}\bigg|_{\varphi(p)} \right)=\frac{\partial \tilde{x}^j}{\partial x^i}(\varphi(p))\frac{\partial}{\partial \tilde{x}^j}\bigg|_{\psi(p)} $$ 座標ベクトルの定義を使うと,次のようになる: \begin{align} \frac{\partial}{\partial x^i}\bigg|_p =&\ d(\varphi^{-1})_{\varphi(p)}\bigg( \frac{\partial}{\partial x^i}\bigg|_{\varphi(p)} \bigg) \\ =&\ d(\psi^{-1})_{\psi(p)} \circ d(\psi\circ\varphi^{-1})_{\varphi(p)}\bigg( \frac{\partial}{\partial x^i}\bigg|_{\varphi(p)} \bigg) \\ =&\ d(\psi^{-1})_{\psi(p)}\bigg( \frac{\partial \tilde{x}^j}{\partial x^i}(\varphi(p))\frac{\partial}{\partial \tilde{x}^j}\bigg|_{\psi(p)} \bigg) = \frac{\partial \tilde{x}^j}{\partial x^i}(\varphi(p))\frac{\partial}{\partial \tilde{x}^j}\bigg|_p \end{align} ここで,$\hat{p} = \psi(p)$と書いている(この式は,$\mathbb{R}^n$における偏微分の連鎖律と全く同じ形なので覚えやすい).ベクトル$v = v^i \frac{\partial}{\partial x^i}\big|_p = \tilde{v}^j \frac{\partial}{\partial \tilde{x}^j}\big|_p$の成分にこの式を適用すると,成分の変換法則は $$ \tilde{v}^j=\frac{\partial \tilde{x}^j}{\partial x^i}(\varphi(p))v^i $$ となる.
接束
多様体上のすべての点における接ベクトル全体の集合を考えることは,しばしば有用である:
接束
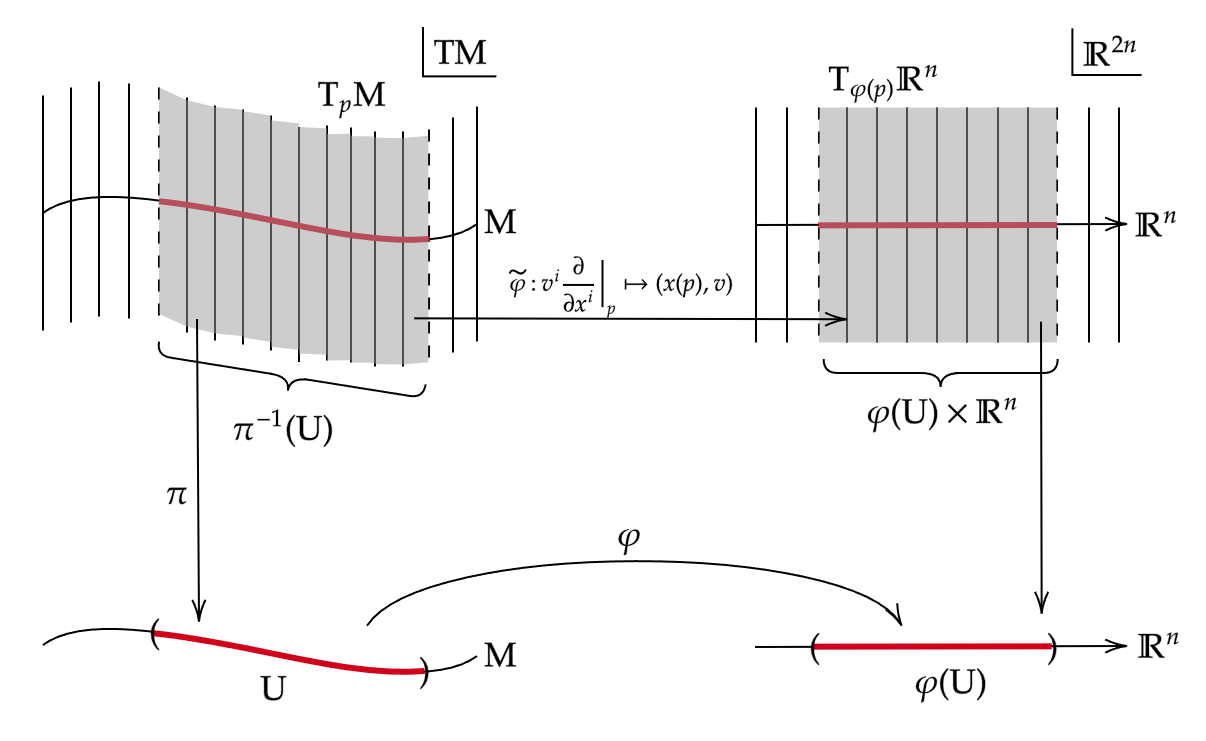
$M$を(境界の有無を問わない)滑らかな多様体とする.$M$の接束(tangent bundle)$TM$とは,$M$のすべての点$p$における接空間$T_p M$の互いに素な和集合 $$ TM = \bigsqcup_{p \in M} T_p M $$ である.
接束の元は,通常,順序対$(p, v)$の形で書く.接束には自然な射影写像(projection map)$\pi: TM \to M$が備わっており,各$T_p M$のベクトルを,それが接している点$p$へ写す:$\pi(p, v) = p$.しばしば,自然な包含写像$v \mapsto (p, v)$を通じて$T_p M$をその像と同一視する.また,強調したい内容に応じて,接ベクトルを$(p, v)$,$v_p$,$v$など様々な記法で表す.
特別な場合として$M = \mathbb{R}^n$のとき,命題より,$\mathbb{R}^n$の接束はその幾何的接空間の合併と自然に同一視でき,それは単に$\mathbb{R}^n$とその自身との直積になる: $$ T\mathbb{R}^n = \bigsqcup_{a \in \mathbb{R}^n} T_a \mathbb{R}^n \cong \bigsqcup_{a \in \mathbb{R}^n} \mathbb{R}^n_a = \bigsqcup_{a \in \mathbb{R}^n} \{a\}\times\mathbb{R}^n \cong \mathbb{R}^n \times \mathbb{R}^n $$ この直積の元$(a, v)$は,幾何的接ベクトル$v_a$や,微分作用素$D_v|_a$のいずれとしても考えることができる.//
一般の滑らかな多様体の接束は,異なる点における接空間同士を自然に同一視する方法が存在しないため,直積として自然に同一視できるとは限らない.
$M$が滑らかな多様体であるとき,接束$TM$は単なるベクトル空間の互いに素な和集合として考えることもできるが,もちろんそれだけではない.次の命題は,$TM$自身もまた滑らかな多様体とみなせることを示している:
任意の滑らかな$n$次元多様体$M$に対して,その接束$TM$には自然な位相と滑らかな構造が入り,$2n$次元の滑らかな多様体となる.この構造のもとで,射影写像$\pi: TM \to M$は滑らかな写像である.
接束の自然座標系
$M$の滑らかなチャート$(U, (x^i))$に対し,$\pi^{-1}(U)$上の写像$\tilde{\varphi}:\pi^{-1}(U)\to\mathbb{R}^{2n}$を $$ \tilde{\varphi}\left( v^i\frac{\partial}{\partial x^i}\bigg|_p \right)=(x^1(p),\ldots,x^n(p),v^1,\ldots,v^n) $$ で定めるとき,この$(x^i, v^i)$を接束の自然座標系(natural coordinate)と呼ぶ.
$M$が(境界の有無を問わない)滑らかな$n$次元多様体であり,$M$が1つの滑らかなチャートで覆われるとき,接束$TM$は$M \times \mathbb{R}^n$と微分同相である.
接束の滑らかな構造を局所的に$U \times \mathbb{R}^n$のような直積空間として図示することは有用だが,すべての接束が大域的に多様体と$\mathbb{R}^n$との積と微分同相(あるいは同相)になると考えてはいけない.実際,ほとんどの滑らかな多様体についてこれは成り立たない.
$F$の微分$dF_p$を$M$のすべての点$p$でまとめることで,接束全体の間の写像が得られる:
大域的な微分
大域的な微分(global differential)とは,各接空間$T_p M \subset TM$への制限が$dF_p$となるような写像$dF:TM\to TN$である.
$F$の微分を特定の接ベクトル$v \in T_p M$に適用する場合,$dF_p(v)$または$dF(v)$のいずれの記法も用いられる.前者は点$p$を強調したいときに,後者は簡潔に書きたいときに使われる.
ここで定義した接束$TM$の滑らかな構造の重要な特徴の一つは,滑らかな写像の微分が,接束間の滑らかな写像になっていることである:
$F: M \to N$が滑らかな写像であるとき,大域微分$dF: TM \to TN$も滑らかな写像である.
大域的な微分の性質として以下のものがある:$M, N, P$を滑らかな多様体とし,$F: M \to N$,$G: N \to P$を滑らかな写像とする.
- $d(G \circ F) = dG \circ dF$である.
- $d(\mathrm{Id}_M) = \mathrm{Id}_{TM}$である.
- $F$が微分同相写像ならば,$dF: TM \to TN$も微分同相写像であり,その逆写像は$(dF)^{-1} = d(F^{-1})$である.