滑らかな多様体
本稿は主に Lee の教科書 [Lee02] に基づいている.また日本語の文献として主に[松本88,中原18]を参考にしている.
「滑らかな多様体」とは局所的にはEuclid空間$\mathbb{R}^n$のように見え,かつ微分や積分ができる空間である.身近な例としては,Euclid空間そのものや,円や放物線のような滑らかな曲線,球面やトーラス,放物面,楕円体,双曲面などの滑らかな曲面である.より高次元の例としては,$\mathbb{R}^{n+1}$内の原点から一定距離にある点の集合($n$次元球面)や,Euclid空間の間の滑らかな写像のグラフなどがある.
より単純な多様体は「位相多様体」であり,これは「局所的に$\mathbb{R}^n$のように見える」という性質のみを持つ位相空間である.しかし,多様体の重要な応用の多くは微積分を伴う.例えば,多様体論の幾何学への応用では,体積や曲率といった性質が関わる.通常,体積は積分によって計算され,曲率は微分によって計算されるため,これらの概念を多様体に拡張するには,多様体上で積分や微分を定義する手段が必須となる.古典力学では,多様体上の常微分方程式系を解くことが求められ,一般相対論では偏微分方程式系を解くことが求められる.
目次
位相多様体
位相多様体
位相空間$M$が次の性質を満たすとき,$M$を$n$次元位相多様体(topological manifold)という:
- $M$はHausdorff空間である.
- $M$は第2可算である.
- $M$は局所的に$n$次元Euclid空間である(後述).
3つ目の性質は,具体的には,各点$p \in M$に対して
- $p$を含む$M$の開集合$U$.($p$の)座標近傍(coordinate neighborhood)という.
- $\mathbb{R}^n$の開集合$\hat{U}$,
- 同相写像$\varphi:U \to \hat{U}$.(局所的な)座標写像(coordinate-map)という.
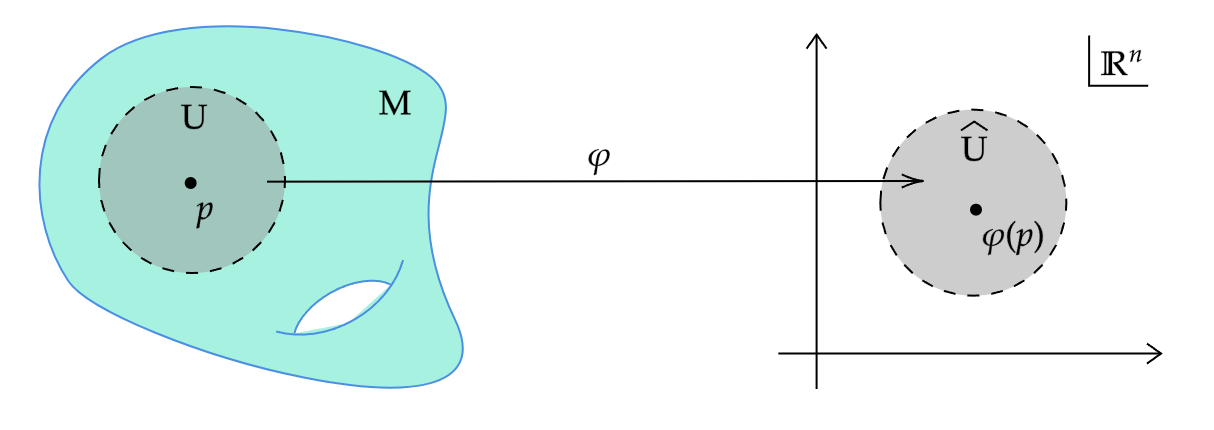
$\varphi(p) = (x_1(p), \ldots, x_n(p))$のように定義される各成分関数$x_1, \ldots, x_n$は$U$上の局所座標(local coordinates)という.
座標写像$\varphi$よりも座標関数$(x_1, \ldots, x_n)$を強調したい場合,チャートを$(U, (x_1, \ldots, x_n))$または$(U, (x_i))$のように表記することもある.
位相多様体の次元(dimension)は以下の定理によりwell-definedであることが示される:
次元の位相不変性
空でない$n$次元位相多様体は,$m = n$のときに限り$m$次元多様体と同相になる.
本によっては位相多様体の定義からHausdorff性や第2可算性,あるいはその両方を省略することもあるが,多様体に関する興味深い結果の多くは実際にこれらの性質を必要とする.また,「自然界」でこれらの仮定のいずれかが成り立たないために多様体でなくなる空間に出会うことは極めて稀なことが知られている.
位相的性質
位相空間として見ると,多様体は非常に特別な存在である.なぜなら,多様体はEuclid空間と多くの重要な性質を共有しているからである.
例えば,$M$を位相多様体とすると,Euclid空間と同様に次のことが成り立つ:
- $M$は局所的に弧状連結である.
- $M$が連結であることと,弧状連結であることは同値である.
- $M$の連結成分は,その弧状連結成分と一致する.
- $M$の連結成分は可算個であり,各連結成分は連結な位相多様体である.
- $M$は局所コンパクトである.
- $M$はパラコンパクトである.
- $M$の基本群は可算である.
位相多様体の例
位相多様体の例としては
- Euclid空間$\mathbb{R}^n$
- 球面$\mathbb{S}^n$
- トーラス$\mathbb{T}^n$
- 射影空間$\mathbb{RP}^n,\mathbb{CP}^n$
滑らかな構造
位相多様体は,多様体のコンパクト性や連結性,単連結性,多様体の同相類の分類問題といった位相的性質を研究するには十分である.しかし,位相多様体の理論全体には微積分の話が一切登場しない.多様体上の関数の微分をどのように定義しようとしても,そのような微分は同相写像の下で不変にはならないからである.
位相多様体$\mathbb{R}^2$上の関数$f:\mathbb{R}^2\to\mathbb{R}$を$f(x,y)=x$により定義する.これは明らかに$\mathbb{R}^2$上で微分可能である.ここで$\mathbb{R}^2$間の写像$\varphi:\mathbb{R}^2\to\mathbb{R}^2$を$\varphi(u,v)=(u^{1/3},v^{1/3})$により定義する.これは同相写像であるが滑らかではない.このとき他方の位相多様体$\mathbb{R}^2$上で関数$f\circ\varphi:\mathbb{R}^2\to\mathbb{R}$は原点で微分可能ではない.//
そこで微分が定義できるように,次のような特別な同相写像を考える:
微分同相写像
逆写像が滑らかな,滑らかな同相写像を微分同相写像(diffeomorphism)という.
滑らかさは同相写像で保たれる性質ではないので,$M$上のすべての滑らかなチャートの集まりを新たな構造として考えなければならない.
変換写像
$M$を$n$次元位相多様体とする.2つのチャート$(U, \varphi)$,$(V, \psi)$が $U \cap V \neq \varnothing$を満たすとき,合成写像$\psi \circ \varphi^{-1} : \varphi(U \cap V) \to \psi(U \cap V)$を変換写像(transition map)という.
変換写像は同相写像の合成なので同相写像である.
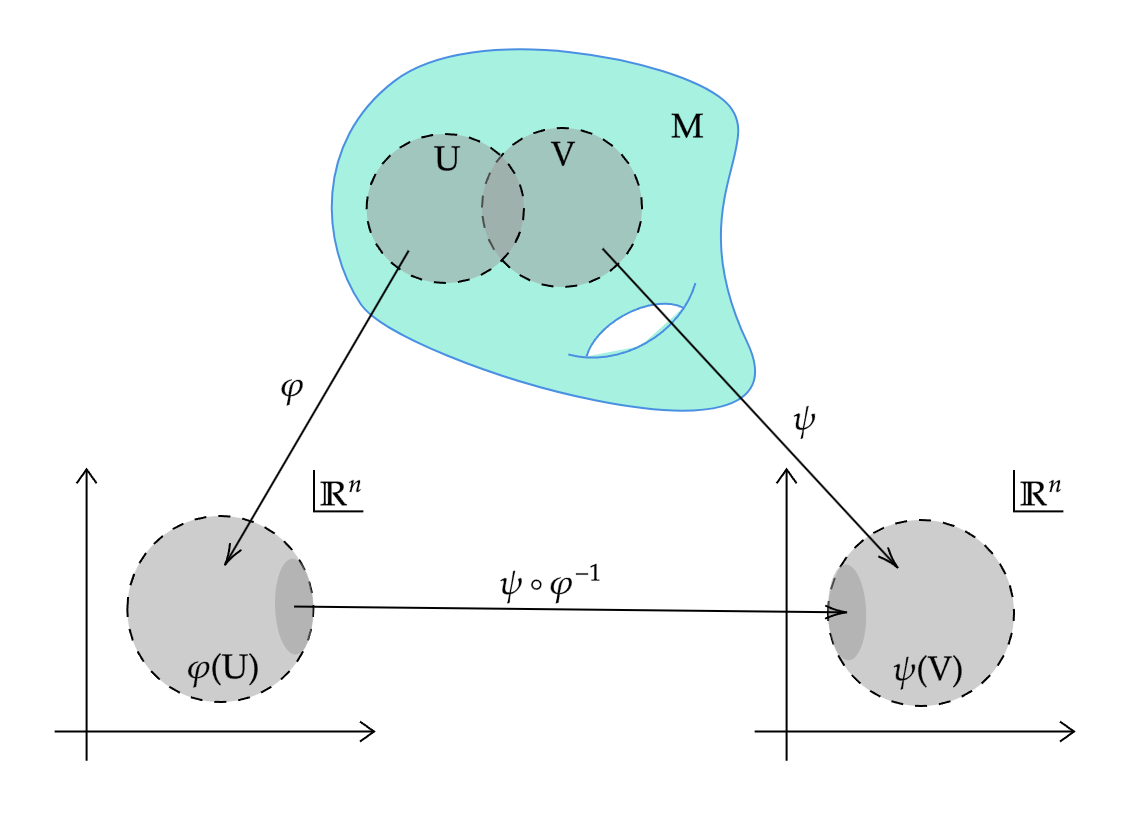
滑らかに両立する
2つのチャート $(U, \varphi)$,$(V, \psi)$が滑らかに両立する(smoothly compatible)とは,$U \cap V = \varnothing$か,または変換写像$\psi \circ \varphi^{-1}$が微分同相写像であることをいう.
(滑らかな)アトラス
位相多様体$M$のアトラス(atlas)$\mathcal{A}$とは,$M$を覆うチャートの集合である.滑らかなアトラス(smooth atlas)とは,$\mathcal{A}$に含まれる任意の2つのチャートが滑らかに両立することをいう.
一般に,ある多様体$M$上には「同じ」滑らかさ構造を与えるアトラスが多数存在する.ここで「同じ」とは,それらのアトラスに含まれるチャートが滑らかに両立する,という意味である.
極大アトラス
位相多様体$M$上の滑らかなアトラス$\mathcal{A}$が極大(maximal)であるとは,$\mathcal{A}$がより大きな滑らかなアトラスに真に含まれないことをいう.極大アトラスを$M$上の滑らかな構造(smooth structure)ともいう.
すなわち,アトラス$\mathcal{A}$に含まれるすべてのチャートと滑らかに両立する任意のチャートは,すでに$\mathcal{A}$に含まれている.そこで極大アトラスは「完備(complete)」である.
任意の位相多様体に滑らかな構造があるとは限らない.
滑らかな多様体
滑らかな多様体とは,位相多様体$M$とその上の滑らかな構造 $\mathcal{A}$との組$(M, \mathcal{A})$である.
滑らかな構造が明らかな場合には,単に「$M$ は滑らかな多様体である」と呼ぶことが多い.
滑らかな構造は,本によっては可微分構造(differentiable structure)や $C^\infty$構造とも呼ばれる.特に日本語の文献では「可微分」という用語がよく使われる.
$M$を位相多様体とする.
- $M$上の任意の滑らかなアトラス$\mathcal{A}$は,$\mathcal{A}$を含む唯一つの滑らかな極大アトラスに含まれる.
- $M$上の2つの滑らかなアトラスが同じ滑らかな構造であることと,それらの和集合が滑らかなアトラスであることは同値である.
例えば,ある位相多様体 $M$ が1つのチャートで覆える場合,滑らかさの両立条件は自動的に満たされるので,そのようなチャートは自動的に $M$ 上の滑らかな構造を定めることになる.
滑らかな構造の概念は,チャートの両立条件を色々変更することで一般化できる.例えば正則性を要請すると「複素多様体」になる.
局所座標表示
$M$を滑らかな多様体とするとき,
- チャート$(U,\varphi)$を滑らかなチャート(smooth chart)という.
- 座標写像$\varphi$を滑らかな座標写像(smooth coordinate map)という.
- 座標近傍$U$を滑らかな座標近傍(smooth coordinate neighborhood)という.
文脈によって「滑らかな」という接頭辞を省略する場合がある.
チャートは次のように捉えると分かりやすい:座標写像$\varphi:U\to\hat{U}$は$U$と$\hat{U}$の間に一時的な同一視を与える.この同一視は,$U$ 上に座標線の逆像として「グリッド」を描くことで視覚化できる.
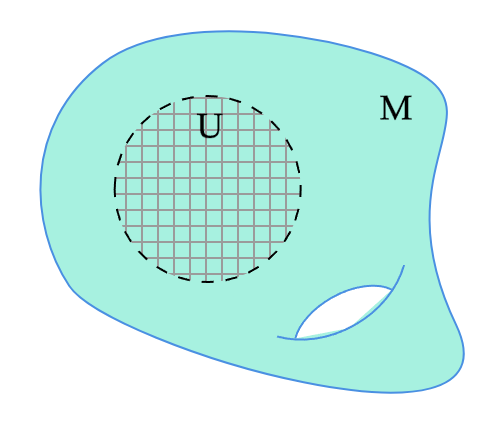
この同一視のもとでは,点$p \in U$をその座標$(x_1, \ldots, x_n) = \varphi(p)$で表し,この$n$組を点$p$そのものとみなすことができる.これを$p$の(局所的な)座標表示(local coordinate representation)という.
多様体にはあらかじめ決まった座標系が存在しないという事実は,長所でもあり短所でもある.座標系をほぼ自由に選べる柔軟性は,多様体論の問題に取り組む際に大きな利点となる.なぜなら,座標系をうまく選ぶことで,問題のある側面を簡単にできる場合が多いからである.しかし,この柔軟性の代償として,多様体上で大域的に定義したい対象が特定の座標系の選び方に依存しないことを証明しなければならない.これには一般に2つの方法がある.
- 座標依存の定義を記述し,その定義がどの座標チャートでも同じ結果を与えることを証明する方法
- 最初から座標に依存しない定義を書く方法
滑らかな多様体を構成するには例えば次のような手順を踏む:
- 位相空間$M$が与えられる.
- $M$が位相多様体であることを確かめる.
- $M$の滑らかな構造を指定する.
しかし,特に最初に位相が与えられていない集合から始める場合には,これらステップを一度にまとめて構成する方が便利なことが多い.次の補題はそのための近道を与えるものである:
集合$M$に対し,$M$の部分集合族$\{U_\alpha\}$と写像$\varphi_\alpha: U_\alpha \to \mathbb{R}^n$が次の性質を満たすとする:
- $\varphi_\alpha$は全単射である.
- $\varphi_\alpha(U_\alpha \cap U_\beta)$および$\varphi_\beta(U_\alpha \cap U_\beta)$は$\mathbb{R}^n$の開集合である.
- $U_\alpha \cap U_\beta \neq \varnothing$のとき,写像$\varphi_\beta \circ \varphi_\alpha^{-1}: \varphi_\alpha(U_\alpha \cap U_\beta) \to \varphi_\beta(U_\alpha \cap U_\beta)$は滑らかである.
- 可算個の$U_\alpha$で$M$を覆う(第2可算性).
- $p, q$を$M$の異なる点とするとき,$p, q$の両方を含む$U_\alpha$が存在するか,または$p \in U_\alpha$, $q \in U_\beta$となる互いに素な$U_\alpha, U_\beta$が存在する(Hausdorff性).
滑らかな多様体の例
滑らかな多様体の例としては
- Euclid空間$\mathbb{R}^n$
- 球面$S^n$
- トーラス$T^n$
- 射影空間$\mathbb{RP}^n,\mathbb{CP}^n$
- 有限次元ベクトル空間$V$
- 行列の空間$M(n,\mathbb{R}),M(n,\mathbb{C})$
- 線形写像の空間$L(V,W)$
- Grassmann多様体$G_k(V)$
境界付き位相多様体
多様体の重要な応用の多く,特に積分を伴うものでは,「境界」を持つ空間に出会うことがある.このような空間を扱うためには,多様体の定義を拡張する必要がある:その一部を$n$次元閉上半空間(closed upper half-space) $$ \mathbb{H}^n=\{x_1,\ldots,x_n\in\mathbb{R}^n \mid x_n\geq0 \} $$ に対応付ける.
境界付き位相多様体
$n$次元境界付き位相多様体(topological manifold with boundary)とは,第2可算かつHausdorffな位相空間$M$であって,$M$の各点が $\mathbb{R}^n$の開集合,または$\mathbb{H}^n$の(相対位相の)開集合と同相な座標近傍を持つものをいう.
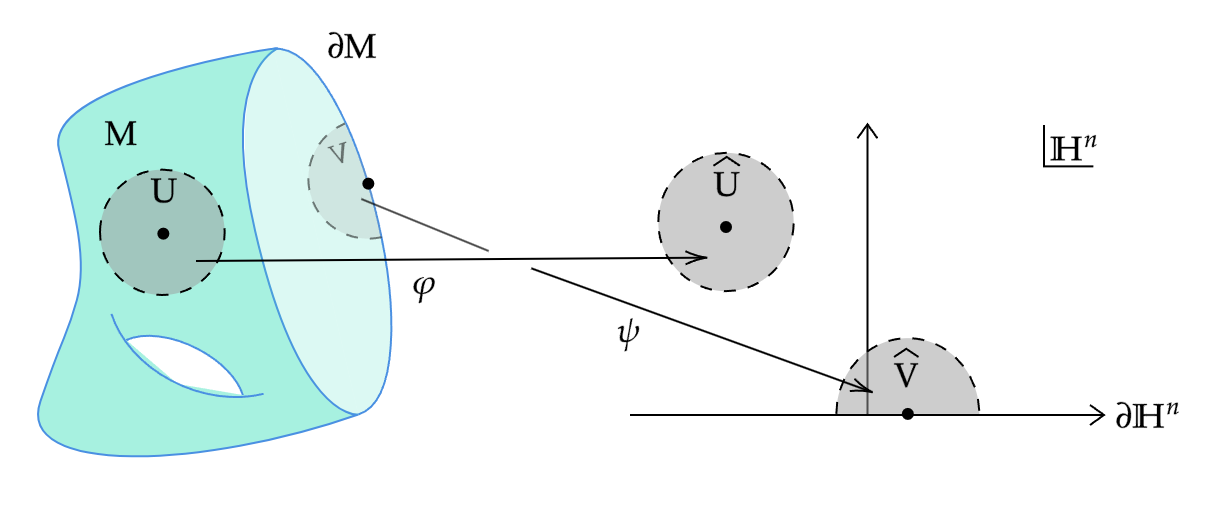
境界付き位相多様体の「境界」や「内部」という概念と,位相空間の部分集合としての「境界」や「内部」という概念との違いに注意する.境界付き位相多様体は,新しい意味で境界が空でない場合があり,それが他の位相空間の部分集合としての境界を持つかどうかとは関係がない.
名前に反して,境界付き位相多様体は一般には多様体ではない.なぜなら,境界点は局所的にEuclid空間と同相な座標近傍を持たないからである.一方,位相多様体は常に境界付き位相多様体であり,その境界は空である.つまり,すべての位相多様体は境界付き位相多様体であるが,境界付き位相多様体が位相多様体となるのは,その境界が空の場合に限る,ということである.
「位相多様体」という用語は,特に断りがない限り,常に境界のない位相多様体を指すことが多い.本稿では,特に断らない限り,この慣習に従う.
文献によって,境界のないコンパクトな位相多様体を「閉多様体(closed manifold)」,境界のない非コンパクトな位相多様体を「開多様体(open manifold)」と呼び分ける場合がある.
境界付き位相多様体$M$の性質は以下の通りである:
- 内部$\mathrm{Int}\,M$は $M$の開部分集合であり,$n$次元位相多様体である.
- 境界$\partial M$は$M$の閉部分集合であり,$(n-1)$次元位相多様体である.
- $n=0$のとき,$\partial M = \varnothing$であり,$M$は0次元多様体である.
- $M$は局所コンパクトである.
- $M$はパラコンパクトである.
- $M$は局所的に弧状連結である.
- $M$の連結成分は可算個であり,各成分は連結な境界付き位相多様体である.
- $M$の基本群は可算である.
境界付き位相多様体上の滑らかな構造
境界付き位相多様体上で滑らかな構造を定義したい.そのためには境界のない場合の定義を自然に拡張すればよい(Émile Borelの補題による):
上半空間上の写像の滑らかさ
$U$を$\mathbb{H}^n$の(相対位相の)開集合とする.写像$F:U\to\mathbb{R}^k$が滑らか(smooth)であるとは,任意の$x\in U$に対して,$x$を含む$\mathbb{R}^k$の開集合$\tilde{U}$と$\tilde{U}$上の滑らかな写像$\tilde{F}:\tilde{U}\to\mathbb{R}^k$が存在し,$F$と$\tilde{F}$が$\tilde{U}\cap\mathbb{H}^n$上で一致することである.
境界付き滑らかな多様体
上述の意味で滑らかな構造を持つ境界付き位相多様体を境界付き滑らかな多様体(smooth manifold with boundary)という.
滑らかな境界付き多様体について,通常の滑らかな多様体の場合に成り立つ重要な結果の一つが,直接には拡張できないことがある.それは有限個の積空間上の滑らかな構造の構成である.なぜなら,半空間$\mathbb{H}^n$と$\mathbb{H}^m$の積 $\mathbb{H}^n \times \mathbb{H}^m$は一般に半空間にはならないため,境界付き滑らかな多様体の有限積は,通常は滑らかな境界付き多様体とはみなせない.しかし,次のような結果は成り立つ:
$M_1, \ldots, M_k$を滑らかな多様体,$N$を境界付き滑らかな多様体とする.このとき,$M_1 \times \cdots \times M_k \times N$は境界付き滑らかな多様体となり, $$ \partial (M_1 \times \cdots \times M_k \times N) = M_1 \times \cdots \times M_k \times \partial N $$ が成り立つ.