滑らかな写像
本稿は主に Lee の教科書 [Lee02] に基づいている.また日本語の文献として主に[松本88,中原18]を参考にしている.
滑らかな構造を導入する主な理由は,多様体上で滑らかな関数や,多様体間の滑らかな写像を定義できるようにするためである.ここではその目的を実現させたい.
目次
滑らかな関数と滑らかな写像
「関数」と「写像」という用語はほぼ同義として用いられるが,滑らかな多様体を扱う際には両者を少し区別すると便利なことが多い.ここでは関数は,値域が $\mathbb{R}$(実数値関数)や $\mathbb{R}^k$(ベクトル値関数,$k > 1$)である写像に使い.写像は,任意の多様体間の写像など,より広い意味で用いることにする.
多様体上の滑らかな関数
多様体上の滑らかな関数
$M$を滑らかな$n$次元多様体,$k$を非負整数,$f: M \to \mathbb{R}^k$を任意の関数とする.$f$が滑らかな関数(smooth function)であるとは,任意の点$p \in M$に対して,$p$を含む$M$の滑らかなチャート$(U, \varphi)$が存在し,合成関数$f \circ \varphi^{-1}$が$\varphi(U) \subset \mathbb{R}^n$上で滑らかであることある.
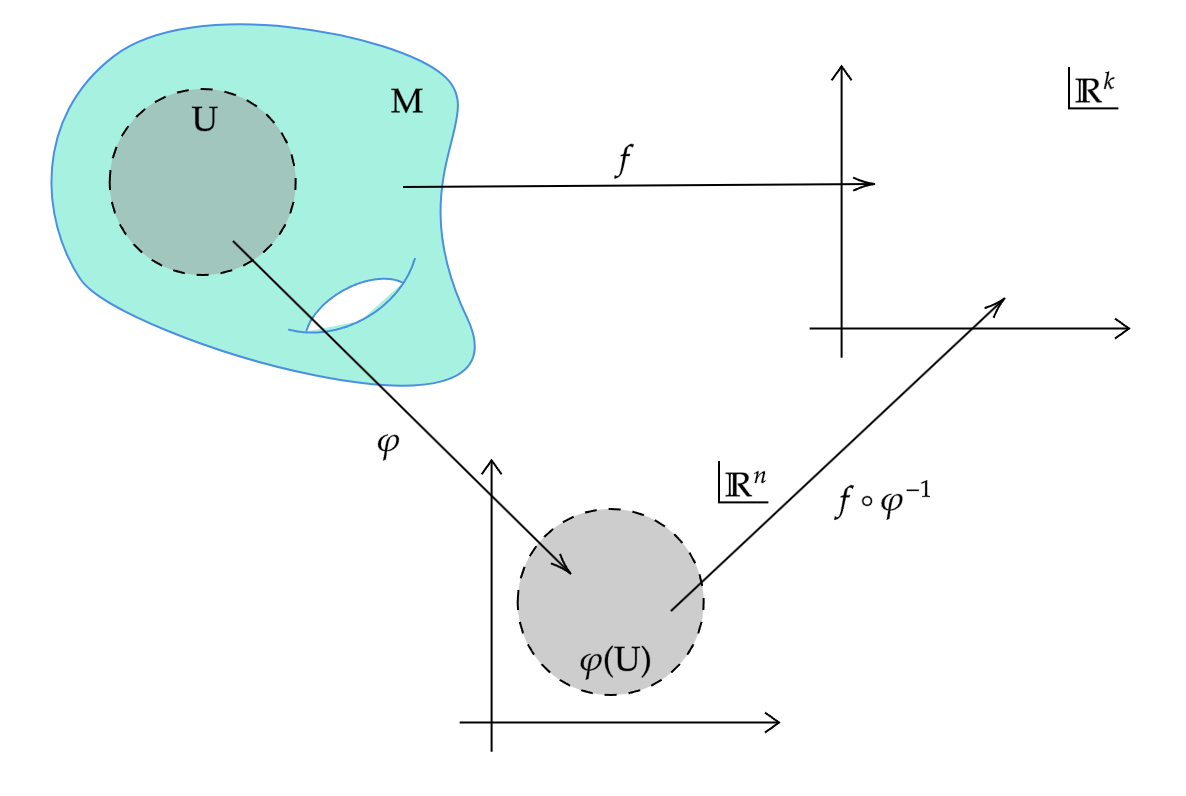
$M$ が境界付き滑らかな多様体である場合も定義は全く同じである.ただし,$U$ は $\mathbb{R}^n$または$\mathbb{H}^n$の開部分集合となり,後者の場合は$f \circ \varphi^{-1}$の滑らかさを前稿の定義のように定める.
多様体上の関数の座標表示
関数$f: M \to \mathbb{R}^k$と$M$上のチャート$(U, \varphi)$が与えられたとき,$f$の座標表示(coordinate representation)とは,$\varphi(U) \subset \mathbb{R}^n$上で定義される関数$f_y(x) = f \circ \varphi^{-1}(x)$のことである.
多様体間の滑らかな写像
滑らかな関数の定義は,多様体間の写像にも自然に一般化できる:
多様体間の滑らかな写像
$M, N$を滑らかな多様体とし,$F: M \to N$を任意の写像とする.$F$が滑らかな写像(smooth map)であるとは,任意の点$p \in M$に対して,$p$を含む$M$の滑らかなチャート$(U, \varphi)$と,$F(p)$を含む$N$の滑らかなチャート$(V, \psi)$が存在し,$F(U) \subset V$かつ合成写像$\psi \circ F \circ \varphi^{-1}$が$\varphi(U)$から$\psi(V)$への滑らかな写像であるときである.
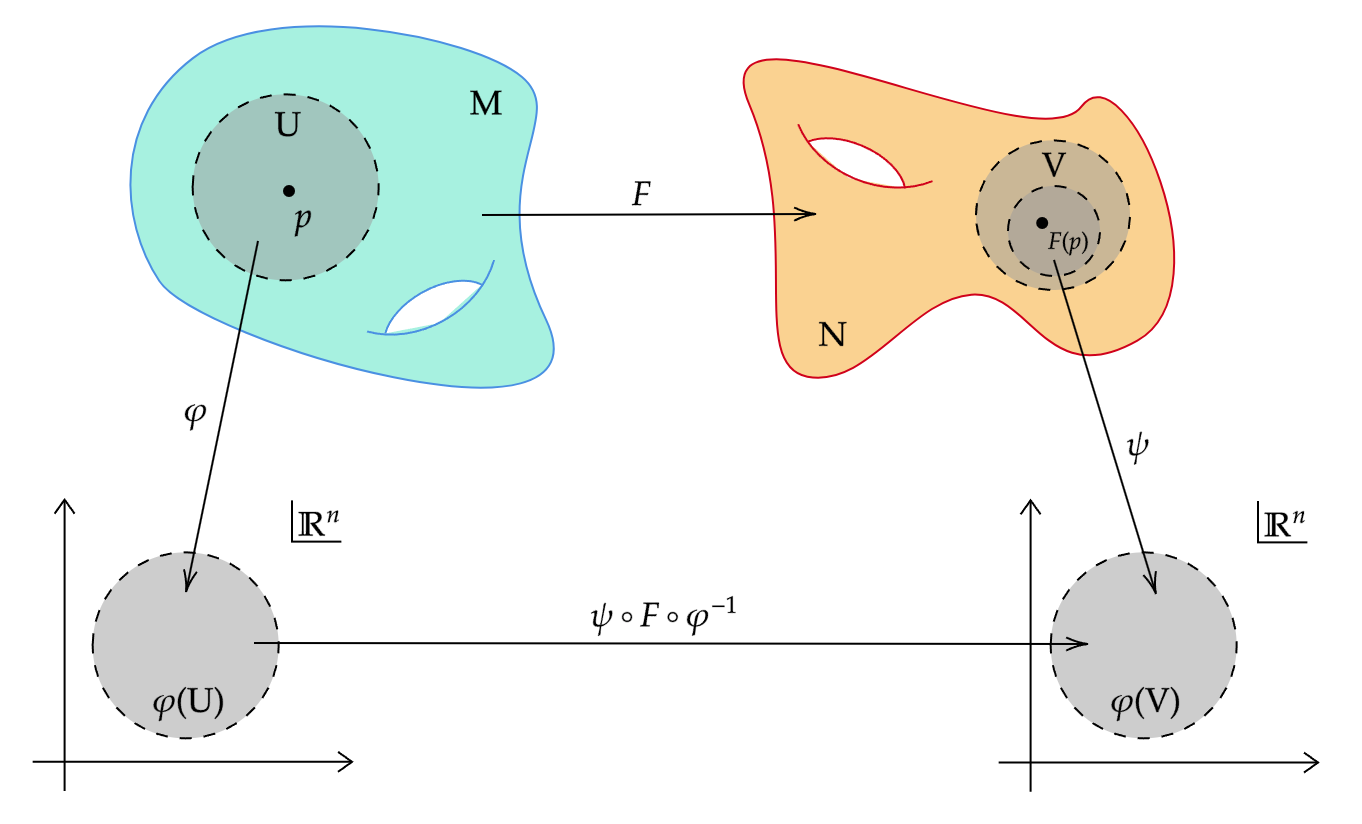
$M$や$N$が境界付き滑らかな多様体の場合も,$F$の滑らかさの定義は全く同じである.ただし,定義域が$\mathbb{H}^n$の部分集合である写像の滑らかさは,各点の近傍で滑らかな写像への拡張が存在することを意味し,値域が$\mathbb{H}^n$の部分集合である場合は,$\mathbb{R}^n$への写像として滑らかであることを意味する.
なお,実数値関数やベクトル値関数の滑らかさの定義は,この定義の特殊な場合とみなすことができる.
期待通り,次のことが成り立つ:
任意の滑らかな写像は連続である.
多様体間の写像の座標表示
$F: M \to N$が滑らかな写像であり,$(U, \varphi)$および$(V, \psi)$がそれぞれ $M$と$N$の任意の滑らかなチャートであるとする.このとき,合成写像$\hat{F} = \psi \circ F \circ \varphi^{-1}$を,与えられた座標系に関する$F$の座標表示(coordinate representation)と呼ぶ.
実数値関数やベクトル値関数の場合と同様に,定義域と値域の両方で具体的な局所座標を選んだ後は,一時的に$F$とその座標表示$\hat{F}$を同一視できる.
次の写像は自動的に滑らかになる:$M,N,P$を(境界の有無を問わない)滑らかな多様体とする.
- 定数写像$c: M \to N$は滑らかである.
- 恒等写像$\mathrm{id}_M: M \to M$は滑らかである.
- $U \subset M$が(境界の有無を問わない)開部分多様体であるとき,包含写像$U \hookrightarrow M$は滑らかである.
- $F: M \to N$および$G: N \to P$ が滑らかならば,合成写像$G \circ F: M \to P$も滑らかである.
$M_1, \ldots, M_k$および$N$を(境界の有無を問わない)滑らかな多様体とし,$M_1, \ldots, M_k$のうち高々1つだけが空でない境界を持つとする.各$i$について,射影$\pi_i: M_1 \times \cdots \times M_k \to M_i$を$M_i$成分への射影とする.写像$F: N \to M_1 \times \cdots \times M_k$が滑らかであることと,各成分写像$F_i = \pi_i \circ F: N \to M_i$が滑らかであることは同値である.
特定の写像が滑らかであることを証明するのは通常それほど難しくない.主に次の3つの方法がよく使われる:
- 便利な局所座標を採り,その成分写像が滑らかな写像の合成であることを示す(上の定理より).
- 既知の滑らかな写像の合成であることを示す.
- 特定の場合に適用できる特別な定理を用いる.
微分同相
ここで微分同相写像の定義を思い出そう.
微分同相
$M$と$N$を(境界の有無を問わない)滑らかな多様体とする.$M$と$N$の間に微分同相写像が存在するとき,$M$と$N$は微分同相であるといい,$M \cong N$と表す.
微分同相写像の性質として次のようなものがある:
- 微分同相写像の合成写像は微分同相写像である.
- 有限個の微分同相写像の積は微分同相写像である.
- 微分同相写像は同相写像かつ開写像である.
- 微分同相写像の(境界の有無を問わない)開部分多様体への制限は,微分同相写像である.
- 微分同相$\cong$は,同値関係である.
2つの位相空間が同相であれば「同じ」とみなされるのと同様に,境界の有無を問わず2つの滑らかな多様体が微分同相であれば本質的に区別できない.滑らかな多様体論の中心的な関心は,微分同相写像によって保存される滑らかな多様体の性質の研究である.
与えられた位相多様体上の滑らかな構造は一意的かどうか?という問は自然である.James MunkresとEdwin Moiseもよって,次元が3以下の任意の位相多様体は,(微分同相なものを除いて)一意な滑らかな構造を持つことが証明されている.
高次元の場合の類似の問題は非常に深く,現在でもほとんど解決されていない.Euclid空間の場合でさえ,滑らかな構造の一意性の問題は20世紀後半まで完全には解決されなかった.その答えは驚くべきものである:$n \neq 4$のとき,$\mathbb{R}^n$は(微分同相なものを除いて)一意な滑らかな構造を持つが,$\mathbb{R}^4$には微分同相でない無数(非可算個)の異なる滑らかな構造が存在する.$\mathbb{R}^4$上の非自明な滑らかな構造の存在は,Simon DonaldsonとMichael Freedmanによって1984年に,コンパクトな4次元多様体の幾何学と位相幾何学に関する彼らの研究の結果として初めて証明された.
コンパクト多様体の場合,状況はさらに興味深いものとなる.1956年,John Milnorは,$\mathbb{S}^7$上に標準的なものと微分同相でない滑らかな構造が存在することを示した.その後,彼とMichel Kervaireは(Steve Smaleの定理を用いて),そのような構造の微分同相類がちょうど15個存在することを示した(「向き」と呼ばれる性質を保存する微分同相写像に制限すると,その微分同相類は28個になる).
一方で4次元以上の次元では,滑らかな構造を全く持たないコンパクトな位相多様体が存在する.4次元位相多様体上に滑らかな構造がいくつ存在するか(もし存在すれば)という問題は,現在も活発に研究されている分野である.
1の分割
位相幾何学でよく使われる道具の一つに「貼り合わせ補題」があり,これは開集合や閉集合上で定義された写像を「貼り合わせて」連続写像を構成する方法を示すものである.滑らかな写像についても,開集合上で定義された滑らかな写像を貼り合わせて滑らかな写像を得るものが存在する.
この貼り合わせ補題の欠点は,適用するためには多様体の部分集合上で写像が完全に一致するように構成しなければならず,これは場合によっては制約が厳しすぎる.そこで「1の分割」という方法を導入する.これは局所的な滑らかな対象を,大域的なものへ「うまく混ぜ合わせる」ための道具であり,重なり合う部分で一致することを必ずしも仮定しなくてよい.1の分割は滑らかな多様体論に不可欠な道具である.
台
$f$を位相空間$M$上の任意の実数値関数またはベクトル値関数とする.$f$の台(support)とは,$f$が$0$でない点全体の集合の閉包 $$ \mathrm{supp}\,f = \overline{\{p \in M \mid f(p) \neq 0\}}. $$ である.$\mathrm{supp}\,f$がある集合$U \subset M$に含まれるとき,$f$は$U$に台を持つ(supported)という.関数$f$の台がコンパクト集合であるとき,$f$はコンパクト台を持つ(compactly supported)という.
次の構成は,第2可算性,パラコンパクト性の最も重要な応用である:
1の分割
$M$を位相空間とし,$\mathcal{X} = \{X_\alpha\}_{\alpha \in A}$を$M$の任意の開被覆とする.$\mathcal{X}$ に従属する1の分割(partition of unity subordinate to $\mathcal{X}$)とは,添字付き関数族$\{\varphi_\alpha\}_{\alpha \in A}$で,$\varphi_\alpha: M \to \mathbb{R}$が連続関数であり,次の性質を満たすものをいう:
- 任意の$x \in M$について,$0 \leq \varphi_\alpha(x) \leq 1$である.
- $\mathrm{supp}\,\varphi_\alpha \subset X_\alpha$である.
- $\{\mathrm{supp}\,\varphi_\alpha\}_{\alpha \in A}$は局所有限である.
- 任意の$x \in M$について,$\sum_{\alpha \in A} \varphi_\alpha(x) = 1$である.
局所有限性(3)のおかげで,(4) の和は各点の近傍で有限個の非零項しか持たず,収束性の問題が生じない.
1の分割の存在
$M$を(境界の有無を問わない)滑らかな多様体とし,$\mathcal{X} = \{X_\alpha\}_{\alpha \in A}$を$M$の任意の開被覆とする.このとき,$\mathcal{X}$に従属する滑らかな1の分割が存在する.
局所的に定義された滑らかな写像を大域的なものへ貼り合わせる方法には,基本的に次の2つの方法がある:
- 各点の近傍ごとに写像を定義し,それらが重なり合う部分で一致するようにできれば,貼り合わせ補題により局所的な定義を大域的な滑らかな写像へとつなぎ合わせることができる.
- 局所的なobjectが重なり合う部分で一致することが保証されない場合は,1の分割を用いる.
後者の場合,「貼り合わせた」objectが必要な性質を保っていることを示す必要がある.