単純Lie代数の表現論
参考文献:H. F. Jones, "Group, Representation and Physics [2nd ed.]", Taylor & Francis, 1998.
Cartan,Weyl,DynkinによるLie代数の一般的な取り扱いは,よく知られた角運動量の代数の一般化である.生成子は互いに可換な集合 $\{H\}$と,それ以外の集合 $\{E\}$ に分けられる.$\{H\}$ の生成子は同時に固有値を割り当てることができ,$\{E\}$ の生成子は一般化された昇降演算子となる.
異なるLie群は,この分割と,$\{H\}$と$\{E\}$の間,そして$\{E\}$同士の非ゼロの交換関係の性質によって体系的に分類できる.この分類は,長さや内積が厳しく制限されたいくつかのルート(単純ルートという)を指定することに相当する.これらの性質はCartan行列,または同等にDynkin図によって要約できる.結果として,Lie代数には4つの無限系列(古典代数という)と,系列に属さない5つの例外的Lie代数が存在することが分かる.
これらのLie代数の表現論も,$\mathfrak{su}(2)$の昇降演算子による取り扱いをモデルとしている.特に,表現の状態 $|j,m\rangle$ は,すべて「最高」の状態 $|j,j\rangle$ に降演算子を適用することで得られた.Cartanの言葉では,これは「最高ウェイト」の状態であり,この概念は複数の可換生成子を持つより複雑なLie代数にも一般化される.
目次
随伴表現とKilling形式
次元 $d$ のLie代数 $L$ は,交換関係で閉じた $d$ 個の生成子 $T_\alpha$ のベクトル空間によって定義される: $$ [T_{\alpha},T_{\beta}] = if^{\gamma}_{\alpha\beta}T_{\gamma} $$ 厳密には,Lie積 $[A, B]$ は必ずしも演算子や行列の交換子とは限らず,$L \times L$ から $L$ への歪対称な写像であり,Jacobi恒等式 $$ [A,[B,C]] + [B,[C,A]] + [C,[A,B]] = 0 $$ を満たす必要がある.$[A, B]$ が交換子である場合,この恒等式は自明に成り立つ.交換子として定義されないLie積の重要な例として,古典力学のHamiltonian形式におけるPoisson括弧がある: $$ [A,B]_{\text{PB}}\equiv \sum_{\alpha}\left(\frac{\partial A}{\partial q_{\alpha}}\frac{\partial B}{\partial p_{\alpha}} - \frac{\partial A}{\partial p_{\alpha}}\frac{\partial B}{\partial q_{\alpha}}\right) $$ この代数はベクトル空間であり,例えば $A_1A + A_2B$ のような線形結合を取ることができる($A_1$ と $A_2$ は通常実数または複素数体の元).Lie積はベクトル空間の加法と両立していなければならず,すなわち $$ [\lambda_1A+\lambda_2B,C]=\lambda_1[A,C]+\lambda_2[B,C] $$ を満たす.
有限群の場合において,固定された元に対する乗法が群の元をちょうど1つずつ組み換わり有限次元表現(正則表現)を与えるのと同様に,Lie代数でも固定された生成子との交換によって生成子自身が写像され,次元 $d$ の表現(随伴表現,$\mathcal{A}$と表記)が得られる.つまり,交換関係において固定された $T_\alpha$ に対し,もう一方の $T_\beta$ は生成子の線形結合へと写像される.この表現では,構造定数自体が生成子の行列要素となる,すなわち $$ (D_{\mathcal{A}}(T_\alpha))^{\gamma}_{\beta} = i f^{\gamma}_{\alpha\beta} $$ ここで,$f$ は $\alpha$ および $\beta$ に関して反対称であることは明らかだが,$\gamma$ については他の2つとは異なる立場にあり,上付き添字で書かれていることに注意.しかし,この添字を「Killing形式」によって下げることで,完全に反対称な $f_{\alpha\beta\gamma}$ を得ることができる.Killing形式は随伴表現を用いて定義される内積であり,今後の解析で非常に有用となる.
Killing形式は次のように定義される: $$ (A,B) \equiv \mathrm{Tr}(D_{\mathcal{A}}(A) D_{\mathcal{A}}(B)) $$ すなわち,随伴表現で$A$と$B$を表す行列の積のトレースである.簡略な記法として,$\mathrm{Tr}_{\mathcal{A}}(AB)$と書くこともある.これを生成子自身に適用すると,Cartan計量$g_{\alpha\beta}$が得られる: $$ g_{\alpha\beta} \equiv \mathrm{Tr}_{\mathcal{A}}(T_\alpha T_\beta) = -f^{\delta}_{\alpha\gamma}f^{\gamma}_{\beta\delta} $$ $g_{\delta\gamma}$を用いて$f^{\delta}_{\alpha\beta}$の添字を下げると, $$ f_{\alpha\beta\gamma} \equiv f^{\delta}_{\alpha\beta}g_{\delta\gamma} $$ となり,これは$\alpha, \beta, \gamma$に関して完全に反対称となる.次に$\mathrm{Tr}_{\mathcal{A}}([T_\alpha, T_\beta], T_\gamma)$を考える.交換子を評価してからトレースを取ると, $$ \mathrm{Tr}_{\mathcal{A}}([[T_\alpha,T_\beta],T_\gamma])=if^{\delta}_{\alpha\beta}\mathrm{Tr}_{\mathcal{A}}(T_\delta T_\gamma)=if_{\alpha\beta\gamma} $$ となる.トレースの巡回性より,次の恒等式が成り立つ: $$ \mathrm{Tr}([A,B]C)=\mathrm{Tr}([B,C]A)=\mathrm{Tr}([C,A]B) $$ よって$f_{\alpha\beta\gamma}=f_{\gamma\alpha\beta}=-f_{\alpha\gamma\beta}$などの関係が得られる.
Lie代数は部分代数を含むことがあり,これは元の生成子の部分空間で,交換関係によって閉じており,また$L$によって生成されるLie群の部分群を生成する.さらに正規部分群は不変部分代数,すなわちイデアルによって生成される.これは,部分空間$I$に含まれるすべての元と$L$の任意の元との交換子が必ず$I$に含まれるような部分空間である:記号的には$[I, L] \subset I$である.Lie代数の基本的な構成要素は単純Lie代数である.これは,零ベクトルや$L$自身以外に非自明なイデアルを持たないLie代数である.一方で半単純Lie代数は,非自明な可換イデアルを持たないLie代数である.
Cartan計量は,Lie代数が半単純かどうかを直接判定することができる.実際,$L$が半単純であるための必要十分条件は,$g$が非退化(すなわち$\det(g) \neq 0$)であることである.あるいは,Killing形式が非退化であること,すなわち$L$のすべての元$X$に対して$(A, X) = 0$が成り立つならば$A=0$であることと同値である.
半単純Lie代数は,単純Lie代数の直和として書けることを示すことができる.もし $L$ が単純であれば,話はそこで終わる.しかし,$L$ がイデアル $I$ を含むと仮定しよう.このとき,Killing形式に関して $I$ と直交する補空間 $P$ を定義する:$(I, P) = 0$.$P$ もベクトル空間であり部分代数となる.さらに, $$ ([P,P]I)=([P,I]P)=(IP)=0 $$ ここで,トレースの巡回性と $I$ がイデアルであることを順に用いた.したがって,$[P, P]$ の任意の元も $I$ と直交する.
次に,$[I, P]$ と他の代数の元との内積を考える.
まず,上と同様に, $$ ([P,I]P)=(IP)=0 $$ 次に, $$ ([P,I]I)=([I,I]P)=(IP)=0 $$ ここでもトレースの巡回性と $I$ の閉性を順に用いている.
したがって,$[P, I]$ は代数のすべての元と直交し,Killing形式が非退化であるため,これはゼロとなる.よって $L = I \oplus P$ である.もし $P$ 自身が単純でなければ,同様の操作を繰り返すことで,最終的に $L$ を複数の単純代数の直和として表すことができる.
実Lie代数の場合,Cartan計量はコンパクト性と非コンパクト性も区別する.$g$が正定値であれば,$L$はコンパクトである.この場合,$g$は対角化でき,スケール変換によって単なる単位行列にすることができる.
Lie代数のCartan基底
構造定数はLie代数を決定するが,その逆は明らかに成り立たない.なぜなら,基底ベクトルを新たに古いものの線形結合として取り直す自由があり,それによって交換関係の表現形式が変わるからである.典型例として,$\mathfrak{su}(2)$代数を考える: $$ [J_i, J_j] = i\varepsilon_{ijk}J_k $$ $J_3$と複素線形結合[1] $J_{\pm} = J_1 \pm iJ_2$ を用いることで,これらは次のように書き換えられる: \begin{align} [J_3, J_{\pm}] =& \pm J_{\pm} \\ [J_{+}, J_{-}] =& 2J_3 \end{align} この形では交換関係はかなり異なって見えるが,もちろん最初の形と完全に同値である.この基底における交換関係は,後の一般化において非常に有用である.
まず,可換な生成子の最大集合を探すことから始める.これは量子力学における表現で望まれるものであり,これらの生成子は通常,同時に固有値を割り当てることができる可換な観測量を表すことになる.$\mathfrak{su}(2)$の場合,可換な生成子は1つだけで,任意に $J_3$ を選ぶことができる.しかし,例えば $\mathfrak{su}(3)$ では,可換な生成子が2つあり,$T_3$ と $T_8$ である.これらは基本表現において,行列 $\frac{1}{2}\mathrm{diag}(1, -1, 0)$ および $\mathrm{diag}(1, 1, -2)/2\sqrt{3}$である.
可換な生成子の最大集合 $\{H_i\}$($i=1,\ldots,r$)はCartan部分代数の基底を形成し,このような生成子の数 $r$ が代数や群の階数となる.これまでに登場したLie群では,$\mathrm{su}(2)$ の階数は1,$\mathrm{su}(3)$ や $\mathrm{su}(4)$ の階数は2である.一般に,$\mathrm{su}(N)$ の階数は $N-1$ であり,これは独立な実の対角成分を持つトレースレスな $N\times N$ 行列の数に等しい.$\{H_i\}$ の同時固有値(ウェイト)は,任意の表現の状態をラベル付けするために用いられる.したがって,交換関係の一部は次のように書ける: $$ [H_i, H_j] = 0 \quad (i, j=1,\ldots,r) $$ 残りの $d-r$ 個の生成子については,線形結合 $\{E_\alpha\}$ をとることで,すべての $H_i$ に対して昇降演算子の性質を持つようにしたい,すなわち $$ [H_i, E_\alpha] \propto E_\alpha \quad (i=r+1,\ldots,d) $$ 別の見方をすれば,交換関係をこの形で書くことができれば,$H_i$ の随伴作用の対角化が達成されたことになる.つまり,$[H_i, X] \propto X$ となり,右辺の係数は $X$ がCartan部分代数に属する場合はゼロとなる.
したがって,我々は次の方程式の固有値 $\lambda$ を求めていることになる: $$ \mathrm{det}(C_{\alpha\beta}-\lambda g_{\alpha\beta}) = 0 $$ ここで $C_{\alpha\beta} = i f_{i\alpha\beta}$($i$ は特定の,固定された添字)であり,最後の添字はKilling形式で下げている.代数が $f$ が実数となるように構成されていると仮定する.この場合,$C$ は純虚数で反対称,すなわちエルミート行列となり,固有値は実数となる.そのうち $r$ 個はゼロ,$d-r$ 個は非ゼロとなる.Cartanの基本定理は,非ゼロ固有値 $(\alpha)_i$ は縮退しない,すなわち各固有値に対応する固有ベクトル $E_\alpha$ は一つだけであることを主張する: $$ [H_i,E_\alpha]=(\alpha)_iE_\alpha $$ この特定の $H_i$ との交換子について,きれいな標準形を得たが,他の交換子はどうなるだろうか?まず $[H_j, E_\alpha]$($j \neq i$)を考える.その $H_i$ との交換子を調べると, $$ [H_i,[H_j,E_\alpha]]=[H_j,[H_i,E_\alpha]]-[E_\alpha,[H_i,H_j]] $$ Jacobi恒等式を用いた.右辺の第2項はゼロであり,第1項は上の式で与えられる.よって $$ [H_i,[H_j,E_\alpha]]=(\alpha)_i[H_j,E_\alpha] $$ したがって $[H_j, E_\alpha]$ は $H_i$ の随伴作用の固有ベクトルであり,固有値は $(\alpha)_i$ である.固有ベクトルが縮退しないので,これは $E_\alpha$ に比例するはずである.比例定数を $(\alpha)_j$ とすると, $$ [H_j,E_\alpha]=(\alpha)_jE_\alpha $$ これは特定の $j$ だけでなく,すべての $j$ について成り立つ.$r$ 次元ベクトル $\alpha \equiv ((\alpha)_1, \ldots, (\alpha)_r)$,$\beta \equiv ((\beta)_1, \ldots, (\beta)_r)$ などは,Lie代数のルートと呼ばれ,対応する固有ベクトル $E_\alpha$ はルートベクトルと呼ばれる.
ルートとルートベクトルの性質
次に自然に生じる疑問は,$E_\alpha$ 同士の交換関係はどうなるか,ということである.これを調べるために,$[H_i, [E_\alpha, E_\beta]]$ を考える.Jacobi恒等式より, \begin{align} [H_i,[E_\alpha,E_\beta]] =& -[E_\alpha,[E_\beta,H_i]] - [E_\beta,[H_i,E_\alpha]] \\ =& (\alpha + \beta)_i[E_\alpha,E_\beta] \end{align} したがって,$[E_\alpha, E_\beta]$ もルートベクトルであり,ルートは $\alpha + \beta$ となる.ただし,$\alpha + \beta = 0$ または $[E_\alpha, E_\beta] = 0$ の場合は例外である.
もし $\alpha + \beta = 0$,すなわち $\beta = -\alpha$ であれば,$[E_\alpha, E_\beta]$ はすべての $H$ と可換となり,Cartan部分代数に属することになる.したがって \begin{align} [E_\alpha, E_{-\alpha}] =& \lambda_i H_i \\ [E_\alpha, E_\beta] =& N_{\alpha\beta} E_{\alpha+\beta} \quad (\beta \neq -\alpha) \end{align} ここで $N_{\alpha\beta}$ は,$\alpha + \beta$ がルートでない場合は $0$ となる.
上の式を書く際,もし $\alpha$ がルートであれば $-\alpha$ もルートであると仮定している.これは,反対称行列 $C$ を含む式の転置を取ることで容易に示すことができる.したがって,ゼロでないルートは $\pm\alpha$ のペアで現れる.これは$\mathfrak{su}(2)$の典型例と同様である.さらに,$H_i$ がエルミートであれば(コンパクト群の場合は必ずそうである),$[H_i,E_\alpha]=(\alpha)_iE_\alpha$より $E_\alpha = E_{-\alpha}^\dagger$ となる.
Cartan基底における交換関係の特別な形から,$\{H_i\}$と$\{E_\alpha\}$の間の内積は非常に単純な性質を持ち,残された基底の再定義の自由度を使って標準形にすることができる.まず$(H_i, E_\alpha)$を考える.トレースの巡回性より,$\mathrm{Tr}_{\mathcal{A}}([H_j, E_\alpha] H_i) = -\mathrm{Tr}_{\mathcal{A}}([H_j, H_i] E_\alpha) = 0$となる.なぜなら$H_j$と$H_i$は可換だからである.一方,左辺は$a_j \mathrm{Tr}_{\mathcal{A}}(E_\alpha H_i)$となり,$a_j \neq 0$なので $$ (H_i,E_\alpha)=0 $$ 同様に,$\alpha+\beta \neq 0$の場合のスカラー積も $$ (E_\alpha,E_\beta) = 0 \quad \alpha+\beta \neq 0 $$ となる.一方,単純Lie代数で計量が非退化(つまりコンパクト)なら$(E_\alpha, E_{-\alpha})$はゼロではなく,適切な規格化によって1とすることができる: $$ (E_\alpha,E_{-\alpha}) = 1 $$ Killing形式が非退化であり,$(H_i,E_\alpha)=0$から基底$\{H_i\}$と$\{E_\alpha\}$でブロック対角になるので,部分行列$(H_i, H_j)$も非退化である.したがって,Cartan部分代数内で適切な変換を施すことで,これを$\delta_{ij}$とすることができる: $$ (H_i,H_j) = \delta_{ij} $$
これらの選択により,$\lambda_i$ は正確に $(\alpha)_i$ となる.したがって,その式の両辺に $H_j$ と内積をとると, $$ ([E_\alpha,E_{-\alpha}],H_j)=\lambda_j $$ ここで $\{H_j\}$ の直交性を用いた.一方,トレースの巡回性を使うと $$ ([E_\alpha,E_{-\alpha}]H_j)=([H_j,E_\alpha]E_{-\alpha})=(\alpha)_j(E_\alpha,E_{-\alpha})=(\alpha)_j $$ これにより $\lambda_j = (\alpha)_j$ であることが示される.
まとめると,Cartan-Weyl基底における生成子の交換関係と内積は次のようになる: \begin{align} [H_i, H_j] =& 0 \\ [H_i, E_\alpha] =& (\alpha)_i E_\alpha \\ [E_\alpha,E_{-\alpha}] =& (\alpha)_i H_i \\ [E_\alpha,E_\beta] =& N_{\alpha\beta}E_{\alpha+\beta} \quad (\alpha+\beta \neq 0) \end{align} また,内積は \begin{align} (H_i, H_j) &= \delta_{ij} \\ (H_i, E_\alpha) &= 0 \\ (E_\alpha, E_{-\alpha}) &= 1 \\ (E_\alpha, E_\beta) &= 0 \quad (\alpha+\beta \neq 0) \end{align} ただし,我々は単純Lie代数がコンパクトであるという仮定を用いていることに注意する.
ルートの「量子化」
各ルート $\alpha$ は $r$ 次元ベクトルであり,成分 $(\alpha)_i$ を持つ.したがって,内積 $\alpha \cdot \beta \equiv (\alpha)_i (\beta)_i$ や $\alpha \cdot H \equiv (\alpha)_i H_i$ を定義できる($i$ について和をとる).後で重要になるので,次のように定義する: $$ H_\alpha \equiv \frac{2}{\alpha^2}\alpha\cdot H $$ ここで,明らかな記法で $\alpha^2$ は $\alpha \cdot \alpha$ を表す.$H_\alpha$ は $H_i$ の線形結合なので,互いに可換である: $$ [H_\alpha, H_\beta] = 0 $$ $[H_i,E_\alpha]=(\alpha)_iE_\alpha$から $$ [H_\alpha,E_\beta]=\frac{2\alpha\cdot\beta}{\alpha^2}E_\beta $$ $[E_\alpha,E_{-\alpha}]=(\alpha)_iH_i$は $$ [E_\alpha,E_{-\alpha}]=\frac{1}{2}\alpha^2H_\alpha $$ 上の式の特殊な場合として $$ [H_\alpha,E_{\pm\alpha}]=\pm2E_{\pm\alpha} $$ これらの最後の2つの式を$\mathfrak{su}(2)生成子の交換関係と比較すると,各 $\alpha$ ごとに$\mathfrak{su}(2)$代数が得られることが分かる.これを $S_\alpha$ と表記し,対応関係は $J_3 \leftrightarrow \frac{1}{2}H_\alpha$,$J_\pm \leftrightarrow (2/\alpha^2)^{1/2}E_{\pm\alpha}$ となる.
この最後の2つの式の意味は,$E_{\pm\alpha}$ が $H_\alpha$ の昇降演算子となり,それぞれ固有値を $\pm2$ だけ上げ下げするということである.$J_3$ の固有値が半整数であったことから,$H_\alpha$ の固有値は整数でなければならない.
さて,他の昇降演算子 $E_\beta$ が $H_\alpha$ に作用する場合を考える.このとき,ステップは $2\alpha \cdot \beta / \alpha^2$ となり,これは整数でなければならない.したがって,重要な性質が得られる: $$ \frac{2\alpha\cdot\beta}{\alpha^2}=n=\text{整数} $$ さらに,これらの整数はSchwarzの不等式によって厳しく制限される.対称な積について $$ \left(\frac{2\alpha\cdot\beta}{\alpha^2}\right)\left(\frac{2\beta\cdot\alpha}{\beta^2}\right) \leq 4 $$ 明らかな方法でベクトル $\alpha$ と $\beta$ の一般化された角度を定義すると $$ \cos{\theta} \equiv \frac{\alpha\cdot\beta}{|\alpha||\beta|} $$ ここで $|\alpha| \equiv \sqrt{\alpha^2}$,同様に $|\beta|$ も定義する.上の関係は $|\cos\theta| \leq 1$ に対応する.整数 $n_1 = 2\alpha \cdot \beta / \alpha^2$ および $n_2 = 2\beta \cdot \alpha / \beta^2$ は $$ n_1 n_2 \leq 4 $$ で制限され,さらに $$ \cos\theta=\frac{1}{2}(n_1 n_2)^{1/2} $$ となる.これにより可能性は限られる.なお,$n_1$ と $n_2$ は必ず同符号なので,便宜上 $0 \leq n_2 \leq n_1$ とする.同様に $0 \leq \theta \leq \pi/2$ とする.他の可能性は $\alpha$ や $\beta$ の符号を反転したり,両者を入れ替えることで得られる.
まず $n_1$ が 4 になることは実際にはあり得ないことに注意する.この場合,$n_2$ は 1 でなければならず,Schwarz の不等式は等号成立となり,$\theta = 0$ となる.実際,$\beta = 2\alpha$ となるが,これは不可能である.いくつかの書籍で述べられていることとは逆に,これは $\beta = \alpha$ として$[H_i,[E_\alpha,E_\beta]]=(\alpha+\beta)_i[E_\alpha,E_\beta]$から導かれるものではない.その場合,この式は単に $0 = 0$ となり,矛盾はしないが,特に有益な情報も与えない.
代わりに,$2\alpha$ がルートであると仮定してみよう.ただし,これは昇演算子 $E_\alpha$ から生成できない場合である.上記から,$3\alpha$ はルートになり得ないので,$[E_\alpha, E_{2\alpha}] = 0$ となる.次に $[E_{-\alpha}, E_{2\alpha}]$ を考える.このとき,
- $[E_{-\alpha}, E_{2\alpha}] = 0$ か,
- $[E_{-\alpha}, E_{2\alpha}] \propto E_\alpha$
- 1.の場合,交換子 $[[E_{-alpha}, E_\alpha], E_{2\alpha}]$ を考えると,Jacobi恒等式よりこれはゼロになる.一方,$[E_\alpha,E_{-\alpha}]=\frac{1}{2}\alpha^2H_\alpha$を使うと,これは $E_{2\alpha}$ に比例することになるので矛盾する.
- 2.の場合も,交換子 $[[E_{-\alpha}, E_{2\alpha}], E_\alpha]$ を考えることで同様の矛盾が生じる.
残りの可能性($n_1 = n_2 = 2$は自明な場合 $\beta = \alpha$ に対応するので除く)は以下の通り:
- $n_1 = 0 \implies n_2 = 0$ の場合は$\theta = \pi/2$ に対応し.2つのルートは直交し,相対的な長さには制限がない.
- $n_1 = n_2 = 1$ の場合,$\theta = \pi/3$ に対応し,$|\alpha| = |\beta|$ となる.
- $n_1 = 2, n_2 = 1$ の場合,$\theta = \pi/4$ に対応し,$|\beta| = \sqrt{2}|\alpha|$ となる.
- $n_1 = 3, n_2 = 1$ の場合,$\theta = \pi/6$ に対応し,$|\beta| = \sqrt{3}|\alpha|$ となる.
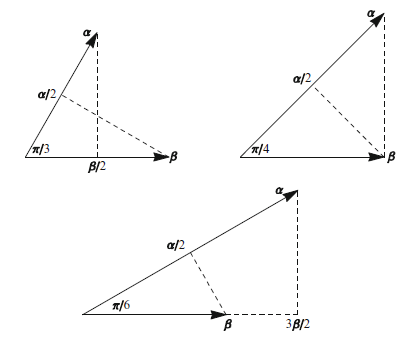
これらの可能性は,階数2の群に対して下図に示されている.ここでルートは2次元ベクトルである.上図には各場合について2つのルートのみが描かれている.では,これらから完全なルート集合をどのように生成するのだろうか?
追加のルートを生成する方法の一つはすでに述べた通りである.それは $E_{\pm\beta}$ を $E_\alpha$ に作用させることで,$\alpha$ を通る $\beta$-ルート列を生成する方法である.このルート列は一般に,$\alpha + p\beta$ から $\alpha - q\beta$ まで,$p$ と $q$ は非負整数として広がる.
このルート列に対応するルートベクトル $E_{\alpha + k\beta}$ は,$S_\beta$ の既約表現の基底を形成し,その次元は $2j + 1$ となる($j$ は整数または半整数).ルート列の両端では,$H_\beta$ の固有値は $\pm j$ となる.すなわち, $$ j E_{\alpha + p\beta} = \left[ \frac{1}{2} H_\beta, E_{\alpha + p\beta} \right] = \frac{(\alpha + p\beta) \cdot \beta}{\beta^2} E_{\alpha + p\beta} $$ よって $$ j = \frac{(\alpha + p\beta) \cdot \beta}{\beta^2} $$ 同様に $$ -j = \frac{(\alpha - q\beta) \cdot \beta}{\beta^2} $$ これから \begin{align} q + p &= 2j \\ q - p &= \frac{2\alpha \cdot \beta}{\beta^2} = n_2 \end{align} 2つ目の式は$2\alpha\cdot\beta/\alpha^2=n$と同値であり,1つ目はルート列の長さを $p$ と $q$ で表している.特に $p = 0$,すなわち $[E_\beta, E_\alpha] = 0$ の場合,重複度は $2j + 1 = q + 1 = n_2 + 1$ となる.同様に,$\beta$ を通る $\alpha$-列の重複度は $n_1 + 1$ である.これらのルート列を用い,各ルートの負号も含めることで,図のダイアグラムを拡張し,下図に示す完全なルート集合を得ることができる.
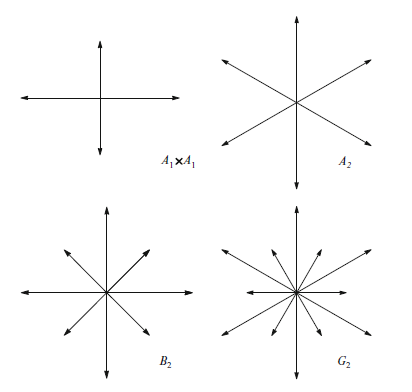
最初の図は単純でない群$S0(4)$に対応しており,これはすでに見たように$SU(2) \times SU(2)$と局所的に同型である.代数は可換な2組の$\mathfrak{su}(2)$ 生成子から成る.2番目の図は $SU(3)$ に対応しており,これにはすでに多少の馴染みがある.ルートは6個,$H$は2個で,必要条件を満たしている.この場合,$n_1 = n_2 = 1$ で,各ルート列の長さは$2$である.もし $[E_\alpha, E_\beta]$ がゼロでなければ,4番目の図が生成されるが,これは例外的群 $G_2$ に対応することが分かっている.3番目の図では $n_1 = 2, n_2 = 1$ で,ルート列の長さはそれぞれ2と3である.$[E_\beta, E_\alpha]$ はゼロでなければならない.なぜなら $\beta + \alpha$ が許された長さや角度のいずれにも該当しないからである.この3番目の図は $S0(5)$ のルートダイアグラムである.
これらのダイアグラムには大きな対称性があることに注意されたい.これはWeyl反射の結果である.Weyl反射は各ルートに対応する$SU(2)$群から生じる.群$S_\alpha$は,昇降演算子を$J_{\pm} = E_{\pm\alpha}/|\alpha|$として同定することで得られる.ここから,$J_2 \equiv (J_+ - J_-)/2i$という演算子を定義でき,これは次の性質を持つ: $$ e^{i\pi J_2}J_3e^{-i\pi J_2}=-J_3 $$ あるいは,$J_3$の同定を考慮すると $$ e^{i\pi J_2}\alpha\cdot He^{-i\pi J_2}=-\alpha\cdot H $$ 一方,$v$が$\alpha$に直交するベクトルであれば,$v\cdot H$には影響しない.なぜなら $$ [v\cdot H,E_{\pm\alpha}]=\pm v\cdot\alpha E_{\pm\alpha}=0 $$ したがって $$ e^{i\pi J_2}v\cdot He^{-i\pi J_2}=v\cdot H $$ よって,$H$の任意の線形結合$x\cdot H$は,$\sigma_\alpha(x)\cdot H$へと変換される.ここで \begin{align} \sigma_{\alpha}(x) =& \left(x-\frac{x\cdot \alpha}{\alpha^2}\alpha\right)-\frac{x\cdot\alpha}{\alpha^2}\alpha \\ =& x - \frac{2x \cdot \alpha}{\alpha^2}\alpha \end{align} 最初の式では$x$を$\alpha$に平行な成分と直交する成分に分解し,平行成分の符号を反転している.幾何学的には,$x$から$\sigma_\alpha(x)$への変換は$\alpha$に直交する平面での反射である.
ここで,任意のルート $\beta$ に対して,そのWeyl反射 $$ \sigma_\alpha(\beta) = \beta - \frac{2\beta \cdot \alpha}{\alpha^2}\alpha $$ もまたルートであることを示したい.これは,$\alpha$ を通るルート列上のルートであることに注意しよう.まず,定義方程式 $$ [x \cdot H, E_\beta] = x \cdot \beta E_\beta $$ を考え,その変換を取ると $$ [\sigma_\alpha(x)\cdot H, \tilde{E}_{\beta}] = x \cdot \beta \tilde{E}_{\beta} $$ となる.ここで $\tilde{E}_{\beta} = e^{i\pi J_2} E_\beta e^{-i\pi J_2}$ である.内積 $x \cdot \beta$ はWeyl反射の下で不変であり,$x \cdot \beta = \sigma_\alpha(x) \cdot \sigma_\alpha(\beta)$ となる.さらに,$y \equiv \sigma_\alpha(x)$ と定義すれば,$y$ も $x$ と同様に任意のベクトルなので,上の式は $$ [y \cdot H, \tilde{E}_{\beta}] = y \cdot \sigma_\alpha(\beta) \tilde{E}_{\beta} $$ となる.これにより,$\sigma_\alpha(\beta)$ もルートであり,対応するルートベクトルは $\tilde{E}_{\beta}$ であることが示される.
Weyl反射とルートの量子化の結果として,2つの異なるルート $\alpha$ と $\beta$ について,次の有用な性質が得られる: \begin{align} \alpha\cdot\beta < 0 \implies& \alpha+\beta \text{ がルート} \\ \alpha\cdot\beta > 0 \implies& \alpha-\beta \text{ がルート} \end{align} 上で列挙した $n_1 \equiv 2\alpha\cdot\beta/\alpha^2$ および $n_2 \equiv 2\beta\cdot\alpha/\beta^2$ の可能性から,$\alpha \neq \beta$ の場合は $n_1$ または $n_2$ のいずれかが $\pm1$ でなければならないことが分かる.もし $\alpha\cdot\beta > 0$ なら,$n_1 = +1$ または $n_2 = +1$ である必要がある.最初の場合は,$\sigma_{\alpha}(\beta)$を使うと $\sigma_\alpha(\beta) = \beta-\alpha$ がルートとなり,もちろんその負号 $\alpha-\beta$ もルートである.2番目の場合は $\sigma_\beta(\alpha) = \alpha-\beta$ となる.もし $\alpha\cdot\beta < 0$ なら,$n_1 = -1$ または $n_2 = -1$ であり,それぞれ適切なWeyl反射によって $\alpha+\beta$ がルートとなる.
単純ルートとDynkin図形
すべてのルートが線形独立であるとは限らない.実際,ルートは$r$次元ベクトルなので,最大でも$r$個しか線形独立にならない.
このような基底を選ぶ非常に有用な方法は,まず「正ルート」と「負ルート」の概念を導入することである.正ルートまたは負ルートとは,最初にゼロでない成分が正または負であるようなルートのことである.この定義により,ルート集合は互いに排他的な2つの集合に分割される.この区分は座標軸の選び方に依存するが,導かれる結果はルートダイアグラムの対称性を除いてその選択に依存しない.
この「正」の概念を用いることで,単純ルートを定義することができる.単純ルートとは,他の2つの正ルートの和として表すことができない正ルートである.これらの単純ルートはルートダイアグラムの基底を形成し[2],任意の正ルート $\alpha$ は $$ \alpha = \sum_{i=1} n_i \alpha_i $$ の形で書くことができる.ただし,非ゼロの $n_i$ はすべて正の整数である.同様に,負ルートも同じ形で表すことができるが,この場合は非ゼロの $n_i$ がすべて負の整数となる.この事実は,ルートが必ずペア $\pm\alpha$ で現れることから,すべての負ルートは何らかの正ルートの符号を反転したものであることによる.
証明は比較的容易である.$\alpha$ が単純ルートであれば自明に成り立つ.そうでなければ,$\alpha$ は2つの正ルートに分解できる:$\alpha = \beta + \gamma$.もし $\beta$ または $\gamma$ のいずれかが単純でなければ,さらに分解できる.この操作を繰り返すことで,最終的に $\alpha$ を正の整数係数を持つ単純ルートの和として表すことができる.
これにより,単純ルートが空間を張ることが示されたが,単純ルートが $r$ 個より多い場合は線形従属になる可能性がある.これが起こらず,単純ルートが正確に $r$ 個であることを証明するための準備として,まず異なる2つの単純ルート $\alpha_i$ と $\alpha_j$ の内積が $\leq 0$ でないことを示す必要がある.
逆に,$\alpha_i \cdot \alpha_j > 0$ であると仮定しよう.このとき,$\alpha\cdot\beta>0\implies\alpha-\beta$はルートであるから $\alpha_i - \alpha_j$ がルートであり,その負号 $\alpha_j - \alpha_i$ もルートであることが分かる.もし $\alpha_i - \alpha_j$ が正ルートであれば,$\alpha_j = \alpha_i + (\alpha_j - \alpha_i)$ と書けるので,$\alpha_j$ が2つの正ルートの和として表され,単純ルートの定義に反する.同様に,$\alpha_j - \alpha_i$ が正ルートであれば,$\alpha_i = \alpha_j + (\alpha_i - \alpha_j)$ と書けるので,やはり矛盾が生じる.
ここで,$\alpha_i$ が線形独立である,すなわち非自明な係数 $c_i$ で $\sum c_i \alpha_i = 0$ となることはない,ということを証明する準備が整った.これも,もしそのような非自明な線形結合が存在すると仮定すると矛盾が生じることを示すことで進める.正ルートの定義から,この和がゼロになるためには,いくつかの係数が正で,他が負でなければならない.一般性を失うことなく,最初の $s$ 個が正,残りが負であると仮定する.この場合,式は次のように書き換えられる: $$ \sum_{i=1}^{s}c_i\alpha_i=\sum_{j=s+1}b_j\alpha_j $$ ここで $c_i$ および $b_j \equiv -c_j$ はともに正である.すると \begin{align} \left(\sum_{i}c_i\alpha_i\right)^2 =& \left(\sum_{i}c_i\alpha_i\right)\cdot\left(\sum_{j}b_j\alpha_j\right) \\ =& \sum_{i,j}c_i b_j \alpha_i \cdot \alpha_j \end{align} しかし,左辺は本質的に正であり,右辺は各 $\alpha_i \cdot \alpha_j \leq 0$ である内積の正の線形結合である.両者が両立する唯一の方法は,すべての係数 $c_i$ および $b_j$ がゼロである場合のみである.
したがって,階数 $r$ の単純Lie代数には正確に $r$ 個の単純ルート $\alpha_i$ があり,他のルートはこれらの単純ルートの整数線形結合として表すことができる.このとき,非ゼロの係数はすべて正の整数か,すべて負の整数となる.
これらの単純ルートはCartan部分代数の自然な基底を定める.すなわち,$H_\alpha \equiv \frac{2}{\alpha^2}\alpha\cdot H$で定義される$H_{\alpha}$であり,これは$\mathfrak{su}(2)$代数$S_{\alpha}$の一部を構成する.この基底(Chevalley基底)では,単純ルートに関する交換関係は次のようになる: \begin{align} [H_{\alpha_i},E_{\alpha_j}] =& \frac{2\alpha_i\cdot\alpha_j}{\alpha_i^2}E_{\alpha_j} \\ [H_{\alpha_i},E_{-\alpha_j}] =& \frac{1}{2}\alpha_i^2\delta_{ij}H_{\alpha_j} \end{align} 後者の交換子は単純ルートの定義から$i=j$の場合以外はゼロとなる.単純ルートに対する$N_{\alpha_i\alpha_j}$は,内積で簡単に計算できる.この基底の唯一の欠点は,$H_{\alpha}$同士が直交しないことである.すなわち,$(H_i,H_j)=\delta_{ij}$より$(H_{\alpha_i}, H_{\alpha_j}) \propto \alpha_i \cdot \alpha_j$となる.
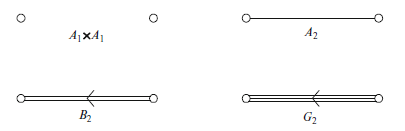
前の図には,階数2の各単純群に対する単純ルートの一つの選び方を示している.単純ルート同士の角度は必ず鈍角でなければならず,これは $\alpha_i \cdot \alpha_j < 0$ であることから分かる.実際,群の代数に関する本質的な情報は,これらの内積にすべて符号化されている.この情報を提示する一つの方法が,次のように定義されるCartan行列である: $$ K_{ij} = \frac{2\alpha_i \cdot \alpha_j}{\alpha_j^2} $$ 対角成分は本質的には冗長であり,$K_{ii} = 2$(和は取らない)となる.すべてのルートの長さが等しければ,$K$ は対称行列となる.単純ルートが線形独立であるため,$K$ は非退化(すなわち $\det(K) \neq 0$)である.$SU(3)$,$SO(5)$,$G_2$ のCartan行列は次の通り: \begin{align} SU(3):&\begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix} \\ SO(5):&\begin{pmatrix} 2 & -1 \\ -2 & 2 \\ \end{pmatrix} \\ G2:&\begin{pmatrix} 2 & -1 \\ -3 & 2 \end{pmatrix} \end{align}
Cartan行列はグラフ形式,すなわちDynkin図形として表現することができる.Dynkin図形では,$r$個の単純ルート$\alpha_i$が小さな円$C_i$として描かれる.任意の2つの円$C_i$と$C_j$は,$n_{ij}$本の線で結ばれる.ここで$n_{ij} = K_{ij}K_{ji}$(和は取らない).以前の議論に戻ると,$n_{ij}$の可能性は0, 1, 2, 3のみであることが分かる.実際,$n_1 = -K_{ij}$,$n_2 = -K_{ji}$と同定できる.
- $n_{ij} = 0$ の場合,ルート同士は結ばれない.
- $n_{ij} = 1$ の場合,ルートは同じ長さを持つ($n_1 = n_2 = 1$).
- $n_{ij} = 2$ の場合,$n_1 = 2, n_2 = 1$ またはその逆となる.
- $n_{ij} = 3$ の場合,$n_1 = 3, n_2 = 1$ またはその逆となる.
長さが異なる場合は,短い方のルートに向かって矢印を描く.
階数2の代数に対応するDynkin図形は下図に示されている.Dynkin図形には,階数$r$が増加する4つの規則的な系列と,系列に属さない5つの特別な図(例外的群に対応し,$G_2$がその最初の例)が存在する.コンパクト群の観点では,4つの規則的系列($A_r$, $B_r$, $C_r$, $D_r$)はそれぞれ$SU(r+1)$,$SO(2r+1)$,$Sp(2r)$,$SO(2r)$の代数に対応する.3番目はシンプレクティック群であり,Hamiltonian形式で重要な役割を持つ.
表現とウェイト
表現とは,代数の元がベクトル空間の状態に作用する方法によって定義される.例えば,$\mathfrak{su}(2)$の場合, \begin{align} J_3|j,m\rangle =& m\hbar |j,m\rangle \\ J_\pm |j,m\rangle =& \hbar\sqrt{(j\mp m)(j\pm m+1)}|j,m\pm 1\rangle \end{align} となる.これにより,$J_3$, $J_+$, $J_-$の表現行列が得られ,そこから$J_1$, $J_2$の行列も導出でき,さらに指数関数化することで群の任意の元の行列が得られる.この$\mathfrak{su}(2)$の表現は有限次元表現であり,$m$の値は$j$までで,最大値$j$の状態は $$ J_{+}|j,j\rangle = 0 $$ を満たす.コンパクトLie群の表現論はこの方法に基づいているが,一般にはCartan部分代数の元$H_i$が複数あり,昇降演算子$E_\alpha$も複数存在する点が異なる.
Cartan部分代数 $H_i$ に関して,表現の状態はそれらの固有値 $\mu_i$ でラベル付けできる: $$ H_i|\mu\rangle=\mu_i|\mu\rangle $$ ウェイト$\mu$は,$r$ 成分のベクトルと考えられ,その成分が $\mu_i$ である.この式の両辺に昇降演算子 $E_\alpha$ を作用させると, $$ E_\alpha|\mu\rangle = E_\alpha\mu_i|\mu\rangle $$ ここで $E_\alpha H_i$ を $[E_\alpha, H_i] + H_i E_\alpha$ と書き,交換関係を用いると, $$ H_i(E_\alpha|\mu\rangle)=(\mu+\alpha)_i(E_\alpha|\mu\rangle) $$ この式は,$E_\alpha$ がウェイト $\mu$ を $\mu+\alpha$ へとシフトすることを示している,すなわち $$ E_\alpha|\mu\rangle \propto |\mu+\alpha\rangle $$ 一般には複数の昇降演算子があり,ウェイトを様々な方向にシフトできる.例えば,さらに $E_\beta$ を作用させると $$ E_\beta E_\alpha|\mu\rangle \propto |\mu+\alpha+\beta\rangle $$ となる.したがって,ウェイト $\mu$ は格子状(ウェイト格子)に並び,$\alpha$ のようなルートによって移動する.ルート格子はウェイト格子の部分集合であり,原点からの移動で得られる.ルートは随伴表現のウェイトに対応する.他の表現では,異なる出発点から移動することでウェイトが生成される.
では,これらの出発点(ウェイト)がどのような条件を満たすべきか調べてみよう.前述の通り, $\frac{1}{2}H_\alpha \equiv \frac{2\alpha \cdot H}{\alpha^2}$ は $\mathfrak{su}(2)$ 代数 $S_\alpha$ の第3成分を構成するので,$H_\alpha$ の固有値は整数でなければならない.$H_i|\mu\rangle=\mu_i|\mu\rangle$より,状態 $|\mu\rangle$ に対する $H_\alpha$ の固有値は $\frac{2\alpha \cdot \mu}{\alpha^2}$ である.したがって, $$ \frac{2\alpha\cdot\mu}{\alpha^2}=\text{整数} $$ もし異なる昇降演算子 $E_\beta$ を作用させて $\mu$ を $\mu + \beta$ にシフトした場合も,$2\alpha \cdot (\mu + \beta)/\alpha^2$ が整数である必要がある.この条件は,確かに満たされる.
前節では,任意のルート $\alpha$ を単純ルート $\alpha_i$ の整数係数による線形結合 $\sum n_i \alpha_i$ で展開できることを説明した.同様の構成がウェイトにも可能であり,この場合の基底は基本ウェイト $\lambda_i$ で定義される: $$ \frac{2\lambda_i\cdot\alpha_j}{\alpha_j^2} = \delta_{ij} $$ 固体物理に詳しい読者は,この構成が本質的に逆格子であることに気付くだろう.一般のウェイト $\mu$ は $$ \mu=\sum_{i=1}^{r}m_i\lambda_i $$ の形で展開でき,ここで係数 $m_i$ は整数でなければならない.この式の両辺に $2\alpha_j/\alpha_j^2$ を内積すると,左辺は整数となり,右辺は $m_j$ だけが残る.
ここからは,ステップ演算子として単純ルート $\alpha_i$ に対応するものを用いることにする.有限次元表現では,$E_{\alpha_i}$ を状態に繰り返し作用させると,あるウェイト $\mu$ で $E_{\alpha_i}|\mu\rangle = 0$ となり,これは $\mathfrak{su}(2)$ 表現の最高状態 $J_+|j,j\rangle = 0$ と同様である.一般のLie群におけるこの状態は最高ウェイト状態と呼ばれ,すべての単純ルートのステップ演算子によって消される,すなわち $$ E_{\alpha_i}|\mu\rangle = 0 \quad i=1, \ldots, r $$ この状態のラベルが表現全体を特徴付けており,$\mathfrak{su}(2)$ の単一ラベル $j$ に相当する.表現の残りの状態は,$E_{-\alpha_i}$($J_-$に相当)を作用させることで得られる.
「最高ウェイト」という表現は,ウェイトが基本ウェイトの整数倍として表されることから生じる.したがって,ウェイトは最初にゼロでない係数 $m_i$ の高さによって順序付けることができる.Dynkin は,ウェイト $\mu$ が既約表現の最高ウェイトとなるための必要十分条件は,すべての整数 $m_i$ が $0$ 以上であることを示した.
このより一般的な手順の具体例として,$\mathfrak{su}(3)$の基本表現を考えてみる.この場合,最高ウェイトは単純ルート $\alpha_1$,または同等に $(m_1, m_2) = (1, 0)$ となる.
前の図に示した座標系をとると,$\alpha_1 = (1, 0)$,$\alpha_2 = (-1, \sqrt{3})/2$(いずれも長さ1に規格化)となる.$\frac{2\lambda_i\cdot\alpha_j}{\alpha_j^2}=\delta_{ij}$を解くと, \begin{align} \lambda_1 =& \frac{1}{2}\bigg(1,\frac{1}{\sqrt{3}}\bigg) \\ \lambda_2 =& \bigg(0,\frac{1}{\sqrt{3}}\bigg) \end{align} となる.ウェイト$\lambda_1$は下図に示されている.その端点は実際には$\alpha_1$と$\alpha_1+\alpha_2$で囲まれる三角形の中心に位置する.他の表現の状態を得るには,$\lambda_1$から$-\alpha_1$や$-\alpha_2$だけシフトできるかどうかを調べる必要がある.
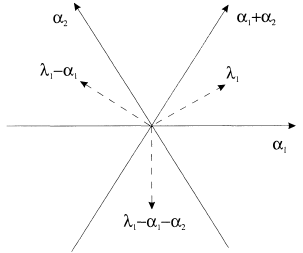
ウェイト $|\mu\rangle$ にステップ演算子 $E_{\pm\beta}$ を作用させると,一般に $|\mu + p\beta\rangle$ から $|\mu - q\beta\rangle$ までの一連のウェイトが生成される.これは,$\alpha$ を通る $\beta$-ルート列と全く同様である.同様の方法で,次の関係が導かれる: \begin{align} q + p &= 2j \\ q - p &= \frac{2\mu \cdot \beta}{\beta^2} \end{align} 基本ウェイト $\lambda_1$ については,$\alpha_1$ と $\alpha_2$ の両方に対して $p = 0$ であることが分かっている.この場合,ウェイト列の長さは $2j + 1 = q + 1 = 2\lambda_1 \cdot \alpha_i / \alpha_j^2 + 1 = m_i + 1$ となり,$\alpha_1$ では 2,$\alpha_2$ では 1 となる.言い換えれば,$\lambda_1$ に $E_{-\alpha_1}$ を作用させて得られる $S_{\alpha_1}$ の表現は二重項,$S_{\alpha_2}$ の表現は一重項となる.したがって,$E_{-\alpha_2}$ は状態 $|\lambda_1\rangle$ を消去し,$E_{-\alpha_1}$ はもう一つウェイト $\lambda_1 - \alpha_1$ を生成する.これは上図に示されている.
次に,この新しい状態に $E_{-\alpha_2}$ を作用させることを考える.この場合も $p = 0$ である.なぜなら,$E_{\alpha_2}(E_{-\alpha_1}|\lambda_1\rangle) = [E_{\alpha_2}, E_{-\alpha_1}]|\lambda_1\rangle + E_{-\alpha_1}E_{\alpha_2}|\lambda_1\rangle$ となり,最初の項の交換子はゼロ,2番目の項は $E_{\alpha_2}|\lambda_1\rangle = 0$ だからである.ウェイト $\mu = \lambda_1 - \alpha_1$ を標準形 $\sum m_i \lambda_i$ で表すと,$m_1 = -1, m_2 = 1$ となる.したがって,この状態は $S_{\alpha_1}$ の下で二重項となり,$E_{-\alpha_2}$ を作用させることでさらにウェイト $\lambda_1 - \alpha_1 - \alpha_2$($m_1 = 0, m_2 = -1$ に対応)を得る.
これで状態の生成は終了である.$E_{\pm\alpha_1}$ を作用させても,これ以上新しい状態は得られない.まず,$E_{\alpha_1}$ を作用させるとウェイト $\lambda_1 - \alpha_2$ が得られるが,これは先に許されないことを示した.したがって,再び $p = 0$ となり,$2j + 1 = m_1 + 1 = 1$ すなわちこの状態は $S_{\alpha_1}$ の下で一重項となる.この表現は,クォーク三重項表現そのものであり,$S_{\alpha_1}$ がアイソスピンの $SU(2)$ に対応する.$SU(2)$ 部分群 $S_{\alpha_2}$ は「U-スピン」と呼ばれ,$SU(3)$ 表現の多くの性質の導出に有効に使われる.ハイパーチャージ $Y$ は $(m_1 + 2m_2)/3$ で与えられる.なお,$\lambda_1$ の高さは1であり,他の2つのウェイトは高さ-1となる.
全く同様の手順で,最高ウェイトが $\lambda_2$ である表現が反クォーク三重項表現($\bar{3}$)であることが示される.これら,そして他の任意の既約表現を識別する方法として,Dynkin図形の各頂点(単純ルート $\alpha_i$ に対応)に整数 $m_i$ を上付きで記入するというものがある.例えば,$\mathfrak{su}(3)$ の2つの基本表現は,下図(a)および(b)のDynkin図形にそれぞれ対応する.

最高ウェイトが $\lambda_1 + \lambda_2$,すなわち $(m_1, m_2) = (1, 1)$ で特徴付けられる表現は,実際には随伴表現である.$\frac{2\lambda_i\cdot\alpha_j}{\alpha_j^2}=\delta_{ij}$から,$\lambda_1 + \lambda_2$ がまさにルート $\alpha_1 + \alpha_2$ であることが分かる.この表現のウェイトは,6つのルートと,2つの縮退したウェイト $\mu = 0$ から成る.これらは状態 $\pi^0$ および八重項 $\eta_8$ に対応する.
ここではこのアプローチとテンソル的アプローチとの対応を詳しく述べる余裕はないが,実際には最高ウェイト($m_1$, $m_2$)で特徴付けられる$\mathfrak{su}(3)$の表現は,既約テンソルによる表現($m = m_1$,$n = m_2$,次元は$(m_1 + 1)(m_2 + 1)(m_1 + m_2 + 2)$)と正確に一致することが示される.
上記の例では,最高ウェイトから始めて既約表現のすべてのウェイトを求める手法を説明したが,表現行列自体を計算するには,$E_\alpha|\mu\rangle\propto|\mu+\alpha\rangle$の比例定数を求める必要がある.これらは,$\mathfrak{su}(2)$ の行列 $D^{(j)}_{m}$ を与える式の係数 $\sqrt{(j \mp m)(j \pm m + 1)}$ に相当する.これらの定数は,漸化式を確立することで計算できる.
次のように書く: $$ E_{-\alpha}|\mu\rangle = N_{-\alpha,\mu}|\mu - \alpha\rangle $$ ここで $$ N_{-\alpha,\mu}=\langle \mu-\alpha | E_{-\alpha}|\mu\rangle $$ とする.期待値 $\langle \mu | [E_\alpha,E_{-\alpha}] | \mu \rangle$ を考えると, $$ \langle \mu | [E_\alpha,E_{-\alpha}] | \mu \rangle = \langle \mu | \alpha\cdot H | \mu \rangle = \alpha\cdot\mu $$ 一方,$E_{-\alpha}=E_{\alpha}^{\dagger}$ の作用を使うと左辺は $|N_{-\alpha,\mu-\alpha}|^2 - |N_{\alpha,\mu}|^2$ となる.さらに,上式の複素共役を取ることで $N_{-\alpha,\mu}^* = N_{\alpha,\mu-\alpha}$ となる.よって $$ |N_{\alpha,\mu-\alpha}|^2-|N_{\alpha,\mu}|^2 = \alpha\cdot\mu $$ したがって,$E_\alpha|\mu\rangle = 0$ となる状態 $|\mu\rangle$ に $E_{-\alpha}$ を繰り返し作用させると,$|\mu\rangle, |\mu-\alpha\rangle, \ldots, |\mu-q\alpha\rangle$ という系列が得られる.ここで $q = 2\mu\cdot\alpha/\alpha^2$ であり,次の差分方程式が成立する: \begin{align} |N_{\alpha,\mu-\alpha}|^2 - 0 =& \alpha\cdot\mu \\ |N_{\alpha,\mu-2\alpha}|^2 - |N_{\alpha,\mu-\alpha}|^2 =& \alpha\cdot(\mu-\alpha) \\ \cdots & \cdots \\ |N_{\alpha,\mu-q\alpha}|^2 - |N_{\alpha,\mu-(q-1)\alpha}|^2 =& \alpha\cdot(\mu-(q-1)\alpha) \\ 0 - |N_{\alpha,\mu-q\alpha}|^2 =& \alpha\cdot(\mu-q\alpha) \end{align} この解は \begin{align} |N_{\alpha,\mu-r\alpha}|^2 =& -\sum_{s=r}^{q}\alpha\cdot(\mu-s\alpha) \\ =& -\frac{1}{2}(q-r+1)(2\alpha\cdot\mu-(q+r)\alpha^2) \\ =& \frac{1}{2}\alpha^2r(q-r+1) \end{align} $q = 2j, r = j - m$ と同定すると,これは $(j - m)(j + m + 1)$ の係数を正しく再現することに注意.位相はこの式では決まらず,一般のLie代数では異なるステップ演算子による系列が重なる場合,位相の整合性に注意が必要である.
本質的に同じ解析を用いて,定数 $N_{\alpha \beta}$ を求めることができることに注意されたい.これらは随伴表現における定数 $N_{\alpha, \mu}$ と同じであり,この場合 $E_\alpha$ は他のステップ演算子 $E_\beta$ に対して交換によって作用する.