Riemann多様体論

目次

• Riemann計量の定義と例
• 接続
• 測地線
• 曲率

Riemann計量の定義と例

この節では，Riemann計量を定義し，それに関連する基本的な対象を構成する．節の終わりでは，非常に対称的な「モデル」となる3種類のRiemann多様体，Euclid空間，球面，双曲空間，を紹介する．これらは今後，理解が深まり道具立てが洗練されるにつれて，繰り返し登場することになる．

Riemann計量は各接空間 $T_pM$ 上に内積を定め，通常 $\langle X, Y \rangle \equiv g(X, Y)$（$X, Y \in T_pM$）と表記される．

混乱の余地がない場合，Riemann計量のことを単に「計量」と呼ぶことがよくある．

等長であることは，Riemann多様体のクラス上で同値関係をなすことは容易に確かめられる．Riemann幾何学は主に，等長写像によって保存される性質を扱う．

$(E_1, \ldots, E_n)$ が $TM$ の任意の局所フレームであり，$(\varphi^1, \ldots, \varphi^n)$ がその双対コフレームであるとき，Riemann計量は局所的に $$ g = g_{ij}\varphi^i \otimes \varphi^j $$ と書ける．係数行列 $g_{ij} = \langle E_i, E_j \rangle$ は $i, j$ で対称であり，$p \in M$ に滑らかに依存する．特に座標フレームの場合，$g$ は $$ g = g_{ij}dx^i \otimes dx^j $$ の形になる．

記法を簡略化するために，2つの1-形式 $\omega$ と $\eta$ の対称積を導入する．これは積記号なしの並置で表される： $$ \omega\eta \equiv \frac{1}{2}(\omega \otimes \eta + \eta \otimes \omega) $$ $g_{ij}$ の対称性により，次のように書き換えられる： $$ g = g_{ij}dx^i dx^j $$

Riemann計量の基本的かつ重要な性質の一つは，ベクトルをコベクトル（1-形式）に，またその逆にも変換できることである．多様体 $M$ 上に計量 $g$ が与えられたとき，「フラット」と呼ばれる写像を $TM$ から $T^*M$ へ定義する．これはベクトル $X$ を次のようなコベクトル $X^{\flat}$ に送る： $$ X^{\flat}(Y) \equiv g(X, Y) $$ 座標表示では， $$ X^{\flat} = g(X^i\partial_i, \bullet) = g_{ij}X^i dx^j $$ 通常，$X^{\flat}$ は $X^{\flat} = X_j dx^j$ と書かれ，ここで $$ X_j \equiv g_{ij}X^i $$ となる．$X^{\flat}$ は $X$ から「添字を下げることで得られる」という（この操作が音楽記号の「フラット」で表される理由である）．

座標基底でのフラットの行列は，計量 $g$ 自身の行列となる．$g$ の行列は可逆なので，フラット写像も可逆である．その逆写像を（他に呼び名がないので）$\omega \mapsto \omega^{\sharp}$（シャープ）と呼ぶ．座標表示では，$\omega^{\sharp}$ の成分は $$ \omega^i \equiv g^{ij}\omega_j $$ となる．ここで $g^{ij}$ は逆行列 $(g_{ij})^{-1}$ の成分である．$\omega^{\sharp}$ は「添字を上げることで得られる」と言う．

シャープ演算子の最も重要な応用の一つは，古典的な勾配（gradient）演算子をRiemann多様体上に拡張することである．

定義を見直すと，$\mathrm{grad}\, f$ は $$ df(Y) = \langle \mathrm{grad}\, f, Y \rangle \quad \text{for all } Y \in TM $$ を満たすことによって特徴付けられ，座標表示では $$ \mathrm{grad}\, f = g^{ij} \partial_i f\, \partial_j $$ となる．

フラットおよびシャープ演算子は，任意の階数のテンソルに対して，任意の添字位置で適用でき，テンソルを共変から反変，またはその逆に変換することができる．例えば，$B$ が3-テンソルである場合，その中間の添字を下げて，共変な3-テンソル $B_{ijk}$ を得ることができる： $$ B_{ijk} \equiv g_{jl}B_{i}{}^{l}{}_{k} $$ 座標に依存しない記法では，これは次のようになる： $$ B^{\flat}(X,Y,Z) \equiv B(X,Y^{\flat},Z) $$ （もちろん，テンソルに複数の上付き添字がある場合，フラット記号だけではどの添字を下げるか分からない．そのような場合は，どの添字を下げるかを言葉で説明する必要がある）．

フラットおよびシャープ演算子のもう一つの重要な応用は，トレース演算子を共変テンソルに拡張することである．ここでは対称な2-テンソルのみを考えるが，これらの結果はより一般的なテンソルにも容易に拡張できる．

計量とは，定義により接ベクトル上の内積である．次の補題が示すように，計量はすべてのテンソル束上にも内積（したがってノルム）を定める．まず用語について説明する．

最後の一般的な構成は，体積要素である．

Riemann体積要素の重要性は，関数だけでなく微分形式の積分も可能にする点にある．$f$ が向き付けられたRiemann多様体 $(M, g)$ 上の滑らかでコンパクト台な関数であるとき，$f\, dV$ はコンパクト台な$n$-形式となる．したがって，積分 $$ \int_M f\, dV $$ は意味を持ち，これを $M$ 上で $f$ を積分したものと定義する．同様に，$M$ の体積は $$ \int_M dV = \int_M 1\, dV $$ で定義される．

接空間上のベクトルの「長さ」を測る方法には，他にもよく使われるものがある．ここで，他の数学分野で重要な役割を果たす3つの方法について簡単に触れておく：擬Riemann計量，部分Riemann計量，Finsler計量である．これらは，Riemann計量の定義における条件を緩和することで定義される．擬Riemann計量は，計量が正定値であるという条件を緩和したものであり，部分Riemann計量は計量が接空間全体で定義されるという条件を緩和したものであり，Finsler計量は各接空間で計量が二次形式であるという条件を緩和したものである．

これは，すべてのベクトルに直交するベクトルがゼロベクトルのみであることを意味する．より形式的には，$g(X, Y) = 0$ がすべての $Y \in T_pM$ について成り立つとき，$X = 0$ である．局所コフレームで $g = g_{ij}\varphi^i\varphi^j$ と書いた場合，非退化性とは行列 $g_{ij}$ が可逆であることを意味する．$g$ がRiemann計量であれば，非退化性は正定値性から直ちに従うので，すべてのRiemann計量は擬Riemann計量でもある．しかし一般には，擬Riemann計量は正定値である必要はない．

擬Riemann計量 $g$ と点 $p \in M$ が与えられたとき，Gram-Schmidtアルゴリズムを少し拡張することで，$g$ が次のような形で表される基底 $(E_1, \ldots, E_n)$ を $T_pM$ 上に構成できる： $$ g = -(\varphi^1)^2 - \cdots - (\varphi^r)^2 + (\varphi^{r+1})^2 + \cdots + (\varphi^n)^2 $$ ここで $0 \leq r \leq n$ は整数である．この整数 $r$ は $g$ の指数と呼ばれ，$g$ が負定値となる $T_pM$ の部分空間の最大次元に等しい．したがって，指数は基底の選び方によらず一定であり，これは古典的にSylvesterの慣性法則として知られている．

Riemann計量以外で最も重要な擬Riemann計量はLorentz計量であり，これは指数が1の擬Riemann計量である．Lorentz計量の最も重要な例はMinkowski計量である．これは $\mathbb{R}^{n+1}$ 上のLorentz計量 $m$ であり，座標 $(\xi^1, \ldots, \xi^n, \tau)$ で次のように書かれる： $$ m = (d\xi^1)^2 + \cdots + (d\xi^n)^2 - (d\tau)^2 $$ 特に $\mathbb{R}^4$ の場合，Minkowski計量はEinsteinの特殊相対性理論の基本的不変量であり，重力がない場合，物理法則はMinkowski計量が上記の形となる任意の座標系で同じ形を持つ，と簡潔に表現できる．「空間」（$\xi$方向）と「時間」（$\tau$方向）の物理的性質の違いは，それぞれが $g$ の上で正定値・負定値となる部分空間であることに由来する．一般相対性理論では，Lorentz計量が点ごとに変化することで重力効果を含めている．

Riemann計量の理論の多くの側面は，擬Riemann計量にも同様に適用できる．擬Riemann幾何学自体は本稿では直接扱わないが，理論のどの部分が擬Riemann計量にも当てはまるかは随時指摘することにする．一般的な目安として，計量テンソルの可逆性のみに依存する証明（例えばRiemann接続や測地線の存在と一意性）は擬Riemannの場合でも問題なく成立するが，正定値性を本質的に用いる証明（例えば測地線の距離最小化性に関するもの）は成立しない．

接続

Riemann多様体上で曲率を定義する前に，測地線（Riemann多様体における「直線」の一般化）を考察する必要がある．測地線を「長さを最小化する曲線」と定義したくなるが，この性質を定義として用いるのは技術的に難しい．そこで，直線の持つ別の性質を選び，それを一般化することにする．

Euclid空間における曲線が「直線」であるための必要十分条件は，その加速度が常にゼロであることである．この性質を，Riemann多様体上の測地線の定義として採用することにする．この考え方を厳密に扱うためには，「接続」と呼ばれる新しい対象を多様体上に導入する必要がある．接続とは，本質的にベクトル場の方向微分を座標に依存せず定めるための規則の集合である．

この節の冒頭では，曲線の加速度に対して不変な解釈を与える問題を詳しく考察し，これが後に続く定義の動機付けとなることを示す．次に，ベクトル束の切断の方向微分という観点から，一般的な「接続」の定義を与える．特に，ベクトル束が接束の場合は「線形接続」と呼ばれ，主にこの場合に焦点を当てて議論を進める．接続の基本的な性質を導出した後，接続を用いて曲線に沿ったベクトル場の微分，測地線の定義，および曲線に沿ったベクトル場の「平行移動」を定義する方法を示す．

なぜ新しい種類の微分演算子が必要なのかを理解するために，$\mathbb{R}^n$ の部分多様体 $M$ とその誘導された Riemann 計量，そして $M$ 内に完全に含まれる滑らかな曲線 $\gamma$ を考える．測地線を「できるだけ真っ直ぐな」曲線として捉えたい．真っ直ぐさを測る直感的な方法は，通常通り Euclid 加速度 $\ddot{\gamma}(t)$ を計算し，それを接空間 $T_{\gamma(t)}M$ へ直交射影することである．これにより，$M$ に接するベクトル $\ddot{\gamma}(t)$（$\gamma$ の接加速度）が得られる．すると，接加速度がゼロであるような曲線を $M$ の測地線と定義できる．この定義は $\mathbb{R}^n$ の剛体運動に対して不変であることは容易に分かるが，この時点ではそれが $M$ のRiemann幾何（誘導計量のみ）に本質的に依存する不変量であるという保証はまだない．

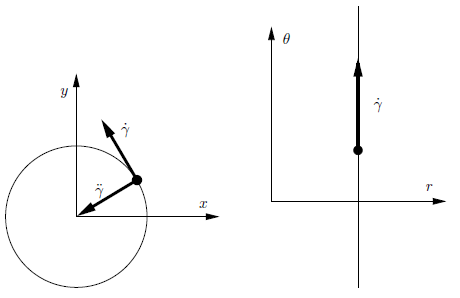
抽象的なRiemann多様体では，「周囲のEuclid空間」が存在せず，その中で微分を行うことができない．そのため，抽象的な多様体内で曲線の加速度を意味付ける方法を見つける必要がある．$\gamma: (a, b) \to M$ をそのような曲線とする．滑らかな多様体理論の研究からわかるように，速度ベクトル $\dot{\gamma}(t)$ は各 $t \in M$ に対して座標に依存しない意味を持ち，その表現は任意の座標系において $\mathbb{R}^n$ 内の曲線の通常の速度の概念と一致する：$\dot{\gamma}(t) = (\dot{\gamma}^1(t), \ldots, \dot{\gamma}^n(t))$．しかし，速度とは異なり，加速度ベクトルにはそのような座標不変の解釈がない．例えば，Euclid座標で $(x(t), y(t)) = (\cos t, \sin t)$ と与えられる平面内の円のパラメータ化された曲線を考えてみる（図4.1）．その時刻 $t$ における加速度は単位ベクトル $(\ddot{x}(t), \ddot{y}(t)) = (-\cos t, -\sin t)$ である．しかし，極座標では，同じ曲線は $(r(t), \theta(t)) = (1, t)$ と記述される（図4.2）．この座標では，加速度ベクトルは $(\ddot{r}(t), \ddot{\theta}(t)) = (0, 0)$ となる．

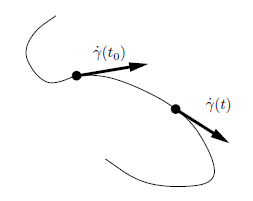
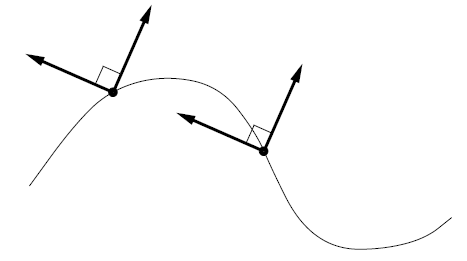
問題は次の通りである：もし $\gamma(t_0)$ を $t$ に関して $\dot{\gamma}(t)$ を微分することで意味付けたい場合，$\dot{\gamma}(t)$ と $\dot{\gamma}(t_0)$ を含む差の商を書かなければならない．しかし，これらは異なるベクトル空間（それぞれ $T_{\gamma(t)}M$ と $T_{\gamma(t_0)}M$）に属しているため，それらを引き算することは意味を成さない（図4.3）．

曲線に沿ったベクトル場の例として速度ベクトル $\dot{\gamma}(t)$ を挙げることができる．この概念については後ほど厳密な定義を与える予定である．多様体内の曲線の加速度を解釈するためには，曲線に沿ったベクトル場を座標に依存しない方法で微分する手段が必要である．そのためには，ベクトル場の値を異なる点で比較する方法，または直感的に言えば，近接する接空間を「接続」する方法が必要である．ここで「接続」が登場する．接続は多様体上の追加のデータであり，ベクトル場の方向微分を計算するための規則を提供する．

接続を定義するには，まずベクトル束の切断を微分する方法として定義するのが最も簡単であることがわかる．後で，その定義を曲線に沿ったベクトル場の場合に適合させることにする．

接続はその大域的な切断への作用によって定義されるが，次の補題が示すように，定義から実際には局所的な演算子であることがわかる．

前の補題は，$p$ における $\nabla_X Y$ を計算するには，$p$ の近くでの $X$ と $Y$ の値を知るだけでよいことを示している．実際，次の補題が示すように，$p$ 自体における $X$ の値を知るだけでよい．

補題より，$\nabla_X Y |_p$ の代わりに $\nabla_{X_p}Y$ と書くことができる．これは，$p$ におけるベクトル $X_p$ の方向への $Y$ の方向微分と考えることができる．

$M$ 上の線形接続は，単に $M$ 上の接続と呼ばれることが多い（アフィン接続という用語も線形接続の同義語として頻繁に用いられるが，一部の著者は両者の間に微妙な区別を設けている）．

線形接続の定義は，(1,2)テンソル場に似ているが，線形接続はテンソル場ではない．なぜなら，$Y$に関して$C^{\infty}(M)$線形ではなく，代わりに積の法則を満たすからである．

次に，線形接続が成分でどのように現れるかを見てみよう．$U \subset M$ を開部分集合とし，$\{E_i\}$ を $TM$ の局所フレームとする．通常は座標フレーム $E_i = \partial_i$ を用いるが，より一般的なフレームで計算を始めるのが有用である．

次の補題は，接続 $\nabla$ の $U$ 上での作用が，そのChristoffel記号によって完全に決定されることを示している．

これまでは接続の性質を研究してきたが，まだ一つも構成していないので，接続が豊富に存在するのか，それとも稀なのか疑問に思うかもしれない．実際には，すぐ後で示すように，接続は非常に豊富に存在する．自明な例から始めよう：$\mathbb{R}^n$ 上で，Euclid接続を次のように定義する． $$ \bar{\nabla}_X(Y^j\partial_j)=(XY^j)\partial_j $$ 言い換えれば，$\nabla_X Y$ は，その成分が $Y$ の成分の $X$ 方向への通常の方向微分であるようなベクトル場である．これが接続に必要な性質を満たすこと，そして標準座標におけるChristoffel記号がすべてゼロであることは容易に確認できる．実際，$\mathbb{R}^n$ 上，あるいは単一の座標近傍で覆われる任意の多様体上には，さらに多くの接続が存在する．次の補題は，それらすべてを明示的に構成する方法を示す．

定義により，$M$上の線形接続とは，ベクトル場の共変微分を計算する方法である．実際には，任意の線形接続は$M$上のすべてのテンソル束上に自動的に接続を誘導し，それによって任意のテンソル場の共変微分を計算する方法が与えられる．

ベクトル場（またはテンソル場）$Y$ の共変微分 $\nabla_X Y$ は，$X$ に関して $C^{\infty}(M)$ 上で線形であるため，これを用いて次のように全共変微分と呼ばれる別のテンソル場を構成することができる．

例えば，$u$ を $M$ 上の滑らかな関数とする．このとき，$\nabla u \in \mathcal{T}^1(M)$ は単に1-形式 $du$ である．なぜなら，両方のテンソルはベクトルに対して同じ作用を持つからである：$\langle \nabla u, X \rangle = \nabla_X u = Xu = \langle du, X \rangle$．2-テンソル $\nabla^2 u = \nabla(\nabla u)$ は $u$ の共変Hessianと呼ばれる．

全共変微分の成分を座標で書くとき，微分から生じる添字を前の添字と区別するためにセミコロンを用いる．したがって，例えば，$Y$ が成分で $Y = Y^i \partial_i$ と書かれるベクトル場である場合，(1,1)テンソル場 $\nabla Y$ の成分は $Y^i{}_{;j}$ と書かれ，次のようになる： $$ \nabla Y=Y^{i}{}_{;j}\partial_i\otimes dx^j $$ ここで $$ Y^{i}{}_{;j}=\partial_j Y^i + Y^k\Gamma^i_{jk} $$ である．より一般的に，次の補題は任意のテンソル場の共変微分の成分の公式を与える．

曲線 $\gamma : I \to M$ があり，区間 $I$ が端点を持つ場合，$\gamma$ の滑らかさとは，定義上，$\gamma$ が $I$ を含むある開区間で定義された滑らかな曲線に拡張できることを意味する．この滑らかさの概念は，（ここでは証明しないが）任意の局所座標における成分関数 $\gamma^i$ が，端点においてすべての階数の片側微分を持つこと，あるいは端点まで連続的に拡張できるすべての階数の微分を持つことと同値であることが示せる．1つまたは2つの端点を持つ区間で定義された滑らかな曲線 $\gamma$ を扱うとき，我々は常に $\gamma$ を少し大きな開区間上の滑らかな曲線に拡張し，その曲線で作業を行い，元の区間に制限して戻すことができる．$\gamma$ の微分の任意の連続関数の $I$ 上での値は，拡張の仕方に依存しない．したがって，証明においては，都合が良いときにはいつでも $\gamma$ が開区間で定義されていると仮定することができる．

上で述べたように，これは座標における通常の速度の概念に対応する．$\gamma$の座標表示を $\gamma(t) = (\gamma^1(t), \ldots, \gamma^n(t))$ と書けば， $$ \dot{\gamma}(t)=\dot{\gamma}^i(t)\partial_i $$ となる（ドットは常にtに関する通常の微分を表す）．

$\mathcal{T}(\gamma)$ で $\gamma$ に沿ったベクトル場の空間を表す．曲線 $\gamma$ に沿ったベクトル場の最も明白な例は，その速度ベクトルである：各 $t$ に対して $\dot{\gamma}(t) \in T_{\gamma(t)}M$ であり，座標表示はそれが滑らかであることを示している．もう一つの例を挙げる：$\gamma$ が $\mathbb{R}^2$ 内の曲線である場合，$N(t) = J\dot{\gamma}(t)$ とする．ここで $J$ は反時計回りに $\pi/2$ の回転であり，したがって $N(t)$ は $\dot{\gamma}(t)$ に直交する．成分で書くと，$N(t) = (-\dot{\gamma}^2(t), \dot{\gamma}^1(t))$ となり，$N$ は $\gamma$ に沿った滑らかなベクトル場である．

多くの例は次の構成によって与えられる：$\gamma : I \to M$ を曲線とし，$\tilde{V} \in \mathcal{T}(M)$ を $M$ 上のベクトル場とする．各 $t \in I$ に対して，$V(t) = \tilde{V}_{\gamma(t)}$ とする．座標で確認すれば，$V$ が滑らかであることは容易にわかる．曲線 $\gamma$ に沿ったベクトル場 $V$ は，$\gamma$ の像の近傍上にベクトル場 $\tilde{V}$ が存在し，このように $V$ と関連付けられるとき，拡張可能であると言われる．曲線に沿ったすべてのベクトル場が拡張可能であるとは限らない．例えば，$\gamma(t_1) = \gamma(t_2)$ であるが $\dot{\gamma}(t_1) \neq \dot{\gamma}(t_2)$ の場合，$\dot{\gamma}$ は拡張可能ではない．

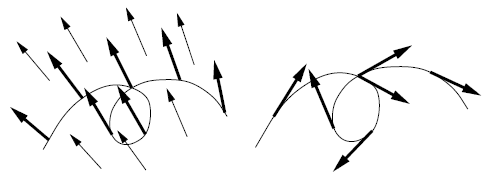
これで，接続の定義を最初に動機付けた問題，すなわち，曲線に沿ったベクトル場の方向微分をどのように意味付ければよいか，という問題に取り組むことができる．

曲線に沿った共変微分の概念ができたので，これで加速度と測地線を定義することができる．

前の定理の一意性の主張から，任意の $p \in M$ と $V \in T_pM$ に対して，$\gamma(0) = p$ と $\dot{\gamma}(0) = V$ を満たす一意的な極大測地線（それ以上大きな区間に延長できないもの）$\gamma : I \to M$ が，ある開区間 $I$ 上に存在することが従う．$I$ はそのような測地線が定義されるすべての開区間の和集合とすればよく，様々な測地線は重なり合う部分で一致することに注意する．この極大測地線は，しばしば単に初期点 $p$ と初期速度 $V$ を持つ測地線と呼ばれ，$\gamma_V$ と表記される（初期点 $p$ は記法で指定する必要はない．なぜなら，$\pi : TM \to M$ を自然な射影とすると，$p = \pi(V)$ によって $V$ から暗黙的に回復できるからである）．

曲線に沿った共変微分を用いる構成には，後で役立つものがもう一つある．それが平行移動である．

平行ベクトル場に関する基本的な事実は，曲線上の任意の点における任意の接ベクトルが，曲線全体に沿った平行ベクトル場に一意的に拡張できるということである．

この定理の証明には，常微分方程式に関する次の基本的な事実が用いられる．すなわち，一般に常微分方程式の解は短時間しか存在を保証できないが，線形方程式の解は常にすべての時間で存在する，というものである．

この節を重要な注意で締めくくる．$\gamma : I \to M$ が曲線で，$t_0, t_1 \in I$ であるとき，平行移動は作用素 $$ P_{t_0t_1}:T_{\gamma(t_0)}M \to T_{\gamma(t_1)}M $$ を，$P_{t_0t_1}V_0 = V(t_1)$ とおくことで定義する．ここで $V$ は $\gamma$ に沿った $V_0$ の平行移動である．これが $T_{\gamma(t_0)}M$ と $T_{\gamma(t_1)}M$ の間の線形同型であることは容易に確認できる（なぜなら，平行性の方程式は線形だからである）．$\gamma$ に沿った共変微分がこの作用素から復元できる．これが，接続が近接する接空間を「接続」するという意味である．

測地線

測地線や共変微分をRiemann幾何学の道具として用いるためには，計量の性質を反映した特定の接続をRiemann多様体上で選び出す方法が必要であることは明らかである．この節では，$\mathrm{R}^n$の部分多様体の例に導かれながら，任意のRiemann多様体上で一意に接続を定める2つの性質について説明する．第1の性質は「計量との整合性」であり，これは動機付けも理解も容易である．第2の性質は「対称性」であり，こちらはやや謎めいている．

Riemann接続とその測地線を定義した後，測地線の集合的な振る舞いを便利に記述する指数写像について調べる．この写像は，初期点や初期ベクトルが変化したときの測地線の変化を研究するのに役立つ．指数写像の性質を確立した後，正規近傍とRiemann正規座標を導入する．最後に，モデルとなるRiemann多様体に戻り，それらの測地線を決定する．

各Riemann多様体上には，Riemann幾何学の計算に特に適した自然な接続が存在することを示す．Riemann多様体に関する我々の直感のほとんどは，誘導計量を持つ$\mathbb{R}^n$の部分多様体を研究することから得られるので，その場合を調べることから始めよう．指導原理として，前節の冒頭で述べた考えを考察しよう：$\mathbb{R}^n$の部分多様体内の測地線は「可能な限り真っ直ぐ」であるべきであり，これはその加速度ベクトル場が$TM$への接射影がゼロであることを意味すると解釈する．

これを接続の言葉で表現するために，$M \subset \mathbb{R}^n$ を埋め込まれた部分多様体とする．$M$ 上の任意のベクトル場は $\mathbb{R}^n$ 上の滑らかなベクトル場に拡張できる．写像 $$ \nabla^{\mathrm{T}}:\mathcal{T}(M) \times \mathcal{T}(M) \to \mathcal{T}(M) $$ を $$ \nabla^{\mathrm{T}}_XY=\pi^{\mathrm{T}}(\bar{\nabla}_XY) $$ と定義する．ここで，$X$ と $Y$ は任意に $\mathbb{R}^n$ に拡張され，$\bar{\nabla}$ は $\mathbb{R}^n$ 上のEuclid接続であり，任意の点 $p \in M$ に対して $\pi^{\mathrm{T}} : T_p\mathbb{R}^n \to T_pM$ は直交射影である．次の補題が示すように，これは $M$ 上の線形接続となり，接接続と呼ばれる．

John Nashによる有名な（そして難しい）定理があり，それによれば，任意の多様体上の任意のRiemann計量は，あるEuclid空間への埋め込みの誘導計量として実現できる．したがって，ある意味では，誘導計量を持つ$\mathbb{R}^n$の部分多様体のみを研究しても一般性を失うことはなく，その場合，接接続で十分であろう．しかし，Riemann多様体の内在的な性質を理解しようとする場合，埋め込みは多くの無関係な情報を導入し，場合によっては，どの幾何学的性質が計量のみに依存するのかを見分けることを実際により困難にする．この節での我々の課題は，接接続の重要な性質の中から，抽象的なRiemann多様体上の接続にとっても意味を持つものを区別し，それらを用いて抽象的な場合に一意的な接続を選び出すことである．

$\mathbb{R}^n$ 上のEuclid接続は，Euclid計量に関して非常に良い性質を一つ持っている：それは次の積の法則を満たす． $$ \bar{\nabla}_X \langle Y,Z \rangle = \langle \bar{\nabla}_X Y, Z \rangle + \langle Y, \bar{\nabla}_X Z \rangle $$ これは標準基底で計算することで容易に確かめられる．もし我々がすべてのベクトル場をMに接するものとして解釈し，内積をM上の誘導計量に関して取られるものとして解釈するならば，接接続も同じ性質を持つことはほとんど直ちにわかる．

この性質は抽象的なRiemann多様体上でも意味を持ち，非常に自然で望ましいものに思えるので，名前が付けられている．

接続が計量と両立することを要求するだけでは，一意的な接続を決定するには不十分であることがわかる．そこで，接接続のもう一つの重要な性質に目を向ける．これは接続の捩率テンソルに関係する．

この証明の利点は，任意の座標チャートにおいてRiemann接続のChristoffel記号を計算するための明示的な公式 $$ \Gamma^{k}_{ij} = \frac{1}{2}g^{kl}(\partial_i g_{jl} + \partial_j g_{il} - \partial_l g_{ij}) $$ が得られることである．

任意のRiemann多様体上では，今後特に断りのない限り，常にRiemann接続を用いることにする．この接続に関する測地線は，Riemann測地線，あるいは混乱の恐れがない限り単に測地線と呼ばれる．

定義から直ちに次の補題が導かれる．

定義のもう一つの帰結は，Riemann接続が座標に依存しない項で定義されているため，等長写像に関してよく振る舞うということである．

この時点では，なぜ対称性がRiemann多様体上の接続に求められる条件なのか，おそらく明らかではないだろう．それを推奨する一つの重要な特徴は，Riemann接続の測地線が局所的に長さを最小化するという事実である．実際，接続の対称性はその証明において決定的な役割を果たす．しかし，この考察だけでは接続が対称であることを強制するものではない．対称性という条件を選び出すより深い理由は，それが上の命題の意味で「自然」であるという事実である．さらに，$\mathbb{R}^n$の埋め込まれた部分多様体上の接接続は対称であり，計量と両立するため，その場合，Riemann接続は接接続と一致しなければならない．この接続が「唯一の」Riemann接続として選ばれた本当の理由はこうである：対称性と両立性は，不変に定義された自然な性質であり，$M$が誘導計量を持つ$\mathbb{R}^n$の部分多様体として実現されるとき（これはNashの埋め込み定理によって常に可能であることが保証されている），接続が接接続と一致することを強制するのである．

曲率

この節では，Riemann計量の局所不変量の研究を始める．すべてのRiemann計量が局所的に等長かどうかという問いから出発し，2階の共変微分が可換でない度合いを測るものとして，Riemann曲率テンソルの定義に至る．そしてこの節の主結果を証明する：多様体の曲率がゼロであることと，それが平坦（すなわち局所的にEuclid空間と等長）であることは同値である．節の最後では，曲率テンソルの基本的な対称性を導き，Ricci曲率およびスカラー曲率を導入する．これらの結果は，擬Riemann計量の場合にも本質的に変わらず適用できる．

Riemann多様体に関する重要な問いは次の通りである：すべてのRiemann多様体は局所的に等長なのだろうか（すなわち，Riemann $n$-多様体 M, $\tilde{M}$ と点 $p \in M$, $\tilde{p} \in \tilde{M}$ が与えられたとき，p の近傍から $\tilde{p}$ の近傍への等長写像は必ず存在するのか）？あるいは，等長写像によって保存されなければならない非自明な局所不変量が存在するのだろうか？これは無意味な問いではない．なぜなら，微分幾何学における多くの興味深く有用な構造は局所不変量を持たないからである．いくつかの例を以下に示す：

• 零でないベクトル場：適切な座標では，すべての零でないベクトル場は局所的に $V = \partial/\partial x^1$ と書くことができるため，それらはすべて局所的に同値である．
• 1-多様体上のRiemann計量：$\gamma : I \to M$ がRiemann 1-多様体の局所的な単位速さのパラメータ付けである場合，$s = \gamma^{-1}$ は計量が $g = ds^2$ という表現を持つ座標チャートを与える．したがって，すべてのRiemann 1-多様体は局所的に $\mathbb{R}$ と等長である．
• シンプレクティック形式：シンプレクティック形式とは，閉じた2-形式 $\omega$ であり，非退化なもの，すなわち，すべての $Y \in T_pM$ に対して $\omega(X, Y) = 0$ となるのは $X = 0$ の場合に限られるものである．Darbouxの定理によれば，すべてのシンプレクティック形式は適切な座標で $\sum dx^i \wedge dy^i$ と書くことができる．したがって，2n-多様体上のすべてのシンプレクティック形式は局所的に同値である．

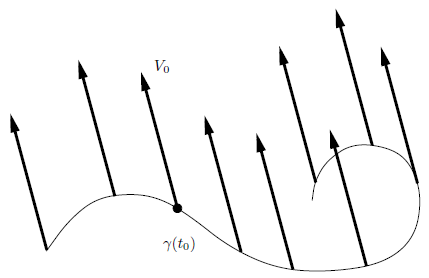
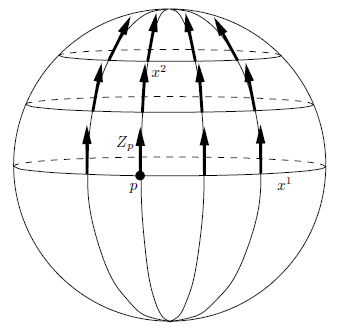
一方，2次元球面とEuclid平面は局所的に等長ではない．その問題の鍵となる考えは，平面内のすべての接ベクトルは平行ベクトル場に拡張できるということであり，したがって，$\mathbb{R}^2$と局所的に等長なRiemann多様体は，局所的に同じ性質を持たなければならない．

Riemann 2-多様体 $M$ が与えられたとき，ベクトル $Z_p \in T_pM$ のそのような拡張を構成しようとする明白な方法がある．$p$ を中心とする任意の局所座標 $(x^1, x^2)$ を選ぶ．まず $Z_p$ を $x^1$ 軸に沿って平行移動し，次に得られたベクトルを $x^2$ 軸に平行な座標線に沿って平行移動する．その結果は，構成上，すべての $x^2$ 座標線および $x^1$ 軸に沿って平行なベクトル場 $Z$ である．問題は，このベクトル場が $x^1$ 軸自身以外の $x^1$ 座標線に沿っても平行であるか，言い換えれば $\nabla_{\partial_1}Z \equiv 0$ が成り立つかである．$x^2 = 0$ のとき $\nabla_{\partial_1}Z$ は消えるので，平行移動の一意性から， $$ \nabla_{\partial_2}\nabla_{\partial_1}Z = 0 $$ を示せば十分である．もし $$ \nabla_{\partial_2}\nabla_{\partial_1}Z = \nabla_{\partial_1}\nabla_{\partial_2}Z $$ が成り立つと知っていれば，構成上 $\nabla_{\partial_2}Z = 0$ が至る所で成り立つため，上式は直ちに従う．実際，$\mathbb{R}^2$ 上では，直接計算すると \begin{align} \nabla_{\partial_2}\nabla_{\partial_1}Z =& \nabla_{\partial_2}(\partial_1 Z^k \partial_k) \\ =& \partial_2\partial_1 Z^k \partial_k \end{align} となり，通常の2階偏微分は可換であるため，$\nabla_{\partial_1}\nabla_{\partial_2}Z$ も同じものに等しい．しかし，上式は任意のRiemann計量に対して成り立つとは限らない．実際，このような2階共変微分の非可換性こそが，この構成が球面上では失敗する原因である．この非可換性の背後には，球面が「曲がっている」という事実が潜んでいる．

この非可換性を座標に依存しない方法で表現するために，量 $\nabla_X\nabla_Y Z - \nabla_Y\nabla_X Z$ を詳しく見てみよう．Euclid平面上では，$X = \partial_1$ かつ $Y = \partial_2$ の場合，これが常に消えることを示したが，任意のベクトル場に対しては，これはもはや真ではないかもしれない．実際，Euclid計量を持つ $\mathbb{R}^n$ では， $$ \nabla_X\nabla_YZ=\nabla_X(YZ^k\partial_k)=XYZ^k\partial_k $$ となり，同様に $\nabla_Y \nabla_XZ = YXZ^k\partial_k$ となる．これら2つの式の差は $(XY Z^k - YXZ^k)\partial_k = \nabla_{[X,Y ]}Z$ である．したがって，$\mathbb{R}^n$ 上のすべてのベクトル場 $X, Y, Z$ に対して次の関係が成り立つ： $$ \nabla_X\nabla_YZ-\nabla_Y\nabla_XZ=\nabla_{[X,Y ]}Z $$ Riemann接続の自然性により，これは $\mathbb{R}^n$ と局所的に等長な任意のRiemann多様体上でも成り立たなければならない．これを「平坦性の判定基準」と呼ぶことにする．

このことから，次のような定義が考えられる．

(3,1)テンソル場として，曲率自己準同型は，1つの上付き添字と3つの下付き添字を持つ任意の局所フレームで書くことができる．最後の添字を反変（上付き）とする規約を採用する（これは，反変添字が先に来るという我々のデフォルトの仮定とは逆である）．したがって，例えば，曲率自己準同型は局所座標 $(x^i)$ を用いて次のように書くことができる． $$ R=R_{ijk}{}^{l} dx^i \otimes dx^j \otimes dx^k \otimes \partial_l $$ ここで，係数 $R_{ijk}{}^{l}$ は次のように定義される． $$ R(\partial_i,\partial_j)\partial_k=R_{ijk}{}^{l}\partial_l $$

ここで，Riemann曲率自己準同型と曲率テンソルの定義で採用されている符号規約に関して，文献によって多くのバリエーションがあることを注意しておくのが適切だろう．ほとんどすべての著者が我々と同じように曲率自己準同型を定義しているが，我々の定義と符号が逆の定義を用いている著者も少数存在する．曲率テンソルの符号については，さらに一致が見られない．曲率自己準同型にどちらの符号を選んだとしても，曲率テンソルは上式のように定義されるが，右辺の$(X, Y, Z, W)$の順列は様々である．しかし，この節の終わりで示す曲率テンソルの対称性を適用すれば，すべての定義は符号を除いて一致する．どちらかの選択を支持する様々な議論があるが，我々は上式を覚えやすくする選択をした．どの本や論文を読み始める際にも，著者の符号規約を確認するように注意する必要がある．

曲率自己準同型と曲率テンソルが興味深い理由の一つは，次の補題によって示される．

曲率テンソルに定性的な幾何学的意味を与えるために，それが局所的にEuclid空間と等長であることへの障害に他ならないことを示す．

Riemann多様体上の曲率テンソルは，最初の2つの引数に関する明らかな歪対称性に加えて，多くの対称性を持つ．

(4)で表される対称性は，（第一）Bianchi恒等式と呼ばれる．これらの対称性を任意の基底に関する成分で書き留めておくと便利である：

1. $R_{ijkl} = -R_{jikl}$
2. $R_{ijkl} = -R_{ijlk}$
3. $R_{ijkl} = R_{klij}$
4. $R_{ijkl} + R_{jkil} + R_{kijl} = 0$

任意のRiemann多様体上の曲率テンソルの共変微分によって満たされる恒等式がもう一つ存在する．古典的には第二Bianchi恒等式と呼ばれるが，現代の著者はより情報量の多い微分Bianchi恒等式という名前を使う傾向がある．

4階テンソルは非常に複雑であるため，曲率テンソルに含まれる情報の一部を要約する，より単純なテンソルを構成することがしばしば有用である．

曲率テンソルに選ばれた符号規約が我々のものと逆である場合，RicciテンソルはRmの第1と第3（または第2と第4）の添字に関するトレースとして定義されなければならないことに注意することが重要である（もちろん，最初の2つまたは最後の2つの添字に関するトレースは，反対称性により常にゼロである）．この定義は，完全な曲率テンソルに対して選ばれた規約に関わらず，Ricci曲率とスカラー曲率が誰にとっても同じ意味を持つように選ばれている．したがって，例えば，多様体が正のスカラー曲率を持つと言われる場合，その意味に曖昧さはない．

Hilbertは，体積が固定された$M$上のすべての計量の空間において，Einstein計量が全スカラー曲率汎関数 $S(g) \equiv \int_M S dV$ の臨界点であることを示した．したがって，Einstein計量は，ある意味で「最適な」計量と見なすことができ，そのようにして，2-多様体上の定Gauss曲率を持つ計量の魅力的な高次元の類似物を形成する．これを用いて，一様化定理のある種の一般化を証明することが期待されるかもしれない．そのような定理の記述は，その2次元の祖先ほどエレガントなものにはなり得ない．なぜなら，Einstein計量を許容しない滑らかでコンパクトな多様体の例が知られているからである．しかし，「ほとんどの」高次元多様体（ある意味で）がEinstein計量を許容するという合理的な希望はまだある．これは活発で広範な現在の研究分野である．

「Einstein計量」という用語は，ご想像の通り，物理学に由来する：Einsteinの一般相対性理論の中心的な主張は，物理的な時空はLorentz計量を持つ4次元多様体でモデル化され，そのRicci曲率が次のEinsteinの場の方程式を満たすというものである： $$ Rc-\frac{1}{2}Sg = T $$ ここで$T$は，時空の各点に存在する物質とエネルギーの密度，運動量，および応力を記述する，ある対称な2-テンソル（エネルギー運動量テンソル）である．物理学の教科書では，上式が，与えられた4次元多様体上のすべてのLorentz計量の空間における，Hilbert作用と呼ばれる特定の汎関数の変分方程式であることが示されている．Einsteinの理論は，物理的に現実的な時空はこの汎関数の臨界点でなければならないという主張として解釈できる．

$T \equiv 0$ の特別な場合，上式は真空のEinstein場の方程式 $Rc = 1/2 Sg$ に帰着する．両辺のトレースを取り，$tr_g g = dim M = 4$ であることを思い出すと，$S = 2S$ を得て，これは $S = 0$ を意味する．したがって，真空のEinstein方程式は $Rc = 0$ と同値であり，これは $g$ が言葉の数学的な意味での（擬Riemann）Einstein計量であることを意味する（理論の発展のある時点で，Einsteinは上式の左辺に項 $\lambda g$ を加えることを考えた．ここで $\lambda$ は彼が宇宙定数と呼んだ定数である．この修正により，真空のEinstein場の方程式は数学者のEinstein方程式と全く同じになる．しかし，Einsteinはすぐに，宇宙定数は物理的な理由から間違いであると判断した）．

これらの特別な場合と，上式とその前の式の間の明らかな形式的類似性を除けば，物理学者のバージョンのEinstein方程式と数学者のバージョンの間に直接的な関係はない．数学的に言えば，Einstein計量が興味深いのは，物理学との関連性のためではなく，高次元における一意化への潜在的な応用のためである．

一様化定理を高次元に一般化するもう一つのアプローチは，定スカラー曲率を持つ計量を探すことである．これらも全スカラー曲率汎関数の臨界点であるが，それは与えられた共形同値類内での計量の変分に関してのみである．したがって，多様体$M$上の計量$g$が与えられたとき，$g$に共形で定スカラー曲率を持つ計量$\tilde{g}$が存在するかどうかを問うことは理にかなっている．これは「山辺問題」と呼ばれている．なぜなら，1960年に山辺英彦が初めてこの問題を提起し，$M$がコンパクトな場合には答えが常に「イエス」であることを証明したと主張したからである．山辺の証明は後に誤りであることが判明し，Richard Schoenによって証明が最終的に完成するまでには24年を要した．$M$が非コンパクトな場合，問題ははるかに微妙になり，現在の研究の多くは，どの共形類が定スカラー曲率を持つ計量を含むかを正確に決定することに焦点を当てている．