Lie群とLie代数
目次
Lie代数
「抽象的な」Lie代数の概念を導入する.あとで各行列Lie群にLie代数を対応させる.Lie代数を表すには,$\mathfrak{g}$や$\mathfrak{h}$などの小文字ゴシック体(Fraktur)文字を用いるのが慣例である(物理では区別を付けない人もいる).
Lie代数
有限次元実または複素Lie代数とは,有限次元の実または複素ベクトル空間$\mathfrak{g}$と,$\mathfrak{g} \times \mathfrak{g}$から$\mathfrak{g}$への写像$[\bullet,\bullet]$が与えられ,以下の性質を満たすものである:
- $[\bullet,\bullet]$は双線型である.
- $[\bullet,\bullet]$は歪対称性を持つ:任意の$X, Y \in \mathfrak{g}$に対して$[X, Y] = -[Y, X]$が成り立つ.
- Jacobi恒等式が成り立つ:任意の$X, Y, Z \in \mathfrak{g}$に対して $$ [X,[Y,Z]]+[Y,[Z,X]]+[Z,[X,Y]]=0 $$
Lie代数$\mathfrak{g}$の元$X, Y$が可換であるとは,$[X, Y] = 0$が成り立つことである.すべての$X, Y \in \mathfrak{g}$について$[X, Y] = 0$が成り立つとき,$\mathfrak{g}$は可換(Abel)Lie代数と呼ばれる.
写像$[\bullet, \bullet]$は$\mathfrak{g}$上のbracket(括弧)演算と呼ばれる.また,条件2より任意の$X \in \mathfrak{g}$について$[X, X] = 0$が成り立つことに注意.Lie代数上のbracket演算は一般には結合的ではないが,Jacobi恒等式は結合性の代替としてみなすことができる.
Jacobi恒等式の証明を注意深く見ると,例えば$XYZ$という項が異なる括り方で2回現れることが分かる.1回は$X(YZ)$,もう1回は$(XY)Z$のようにである.これは任意のLie代数において,Jacobi恒等式はbracket演算が,実際にそう定義されていなくても,ある結合代数における$XY - YX$のように振る舞うことを意味する.実際,任意のLie代数$\mathfrak{g}$が結合代数$\mathcal{A}$に埋め込まれ,そのbracket演算が$XY - YX$となるようにできることが示せる(Poincaré-Birkhoff-Witt定理).
特に重要なのは,$\mathcal{A}$がすべての$n \times n$複素行列からなる空間$M_n(\mathbb{C})$である場合である.
部分代数
実または複素Lie代数$\mathfrak{g}$の部分代数とは,$\mathfrak{g}$の部分空間$\mathfrak{h}$であって,任意の$H_1, H_2 \in \mathfrak{h}$に対して$[H_1, H_2] \in \mathfrak{h}$が成り立つものである.$\mathfrak{g}$が複素Lie代数で,$\mathfrak{h}$が$\mathfrak{g}$の実部分空間かつbracket演算で閉じている場合,$\mathfrak{h}$は$\mathfrak{g}$の実部分代数と呼ばれる.
イデアル
Lie代数$\mathfrak{g}$の部分代数$\mathfrak{h}$が,任意の$X \in \mathfrak{g}$と$H \in \mathfrak{h}$に対して$[X, H] \in \mathfrak{h}$を満たすとき,$\mathfrak{h}$は$\mathfrak{g}$のイデアルと呼ばれる.
中心
Lie代数$\mathfrak{g}$の中心とは,すべての$Y \in \mathfrak{g}$に対して$[X, Y] = 0$となる$X \in \mathfrak{g}$全体の集合である.
Lie代数準同型
$\mathfrak{g}$と$\mathfrak{h}$がLie代数であるとき,線型写像$\varphi: \mathfrak{g} \to \mathfrak{h}$が,すべての$X, Y \in \mathfrak{g}$に対して$\varphi([X, Y]) = [\varphi(X), \varphi(Y)]$を満たすとき,$\varphi$はLie代数準同型と呼ばれる.さらに,$\varphi$が全単射(一対一かつ全射)である場合,$\varphi$はLie代数同型と呼ばれる.Lie代数自身へのLie代数同型はLie代数自己同型と呼ばれる.
随伴表現
$\mathfrak{g}$がLie代数で$X$が$\mathfrak{g}$の元のとき,線型写像$\mathrm{ad}_X: \mathfrak{g} \to \mathfrak{g}$を $$ \mathrm{ad}_X(Y) = [X, Y] $$ により定義する.写像$X \mapsto \mathrm{ad}_X$は随伴写像または随伴表現と呼ばれる.
$\mathrm{ad}_X(Y) = [X, Y]$という形で随伴写像を定義したが,この「ad」記法は計算上便利である.例えば, $$ [X,[X,[X,[X,Y]]]] $$ のような式は, $$ (\mathrm{ad}_X)^4 Y $$ と簡潔に書ける.このような記法は後で本質的になる.また,随伴写像$\mathrm{ad}$(すなわち$X \mapsto \mathrm{ad}_X$)は$\mathfrak{g}$から$\mathrm{End}(\mathfrak{g})$($\mathfrak{g}$上の線型写像全体の空間)への線型写像とみなせる.このとき,Jacobi恒等式は$\mathrm{ad}_X$がbracket演算の「微分作用素」であることと同値になる: $$ \mathrm{ad}_X([Y, Z]) = [\mathrm{ad}_X(Y), Z] + [Y, \mathrm{ad}_X(Z)] $$
随伴表現は表現
$\mathfrak{g}$がLie代数であるとき, $$ \mathrm{ad}_X([Y,Z]) = \mathrm{ad}_X \mathrm{ad}_Y - \mathrm{ad}_Y \mathrm{ad}_X = [\mathrm{ad}_X, \mathrm{ad}_Y] $$ すなわち,$\mathrm{ad}: \mathfrak{g} \to \mathrm{End}(\mathfrak{g})$はLie代数準同型である.
Lie代数の直和
$\mathfrak{g}_1$と$\mathfrak{g}_2$がLie代数であるとき,$\mathfrak{g}_1$と$\mathfrak{g}_2$の直和は,ベクトル空間としての直和$\mathfrak{g}_1 \oplus \mathfrak{g}_2$に,bracket演算 $$ [(X_1, X_2), (Y_1, Y_2)] = ([X_1, Y_1], [X_2, Y_2]) $$ を定めたものである.また,$\mathfrak{g}$がLie代数で,$\mathfrak{g}_1$と$\mathfrak{g}_2$がその部分代数であるとき,$\mathfrak{g}$がベクトル空間として$\mathfrak{g}_1 \oplus \mathfrak{g}_2$に分解され,すべての$X_1 \in \mathfrak{g}_1$と$X_2 \in \mathfrak{g}_2$について$[X_1, X_2] = 0$が成り立つとき,$\mathfrak{g}$は$\mathfrak{g}_1$と$\mathfrak{g}_2$のLie代数の直和に分解されるという.
bracket演算が$\mathfrak{g}_1 \oplus \mathfrak{g}_2$をLie代数にすることは容易に確かめられる.また,$\mathfrak{g}$が部分代数$\mathfrak{g}_1$と$\mathfrak{g}_2$のLie代数の直和に分解される場合,$\mathfrak{g}$はLie代数として「抽象的な」直和$\mathfrak{g}_1 \oplus \mathfrak{g}_2$と同型であることも容易に分かる(このとき,$\mathfrak{g}_1$の任意の元と$\mathfrak{g}_2$の任意の元が可換であるという仮定がなければ,この同型は成り立たない).
構造定数
$\mathfrak{g}$を有限次元の実または複素Lie代数とし,$X_1, \ldots, X_N$を$\mathfrak{g}$の基底(ベクトル空間として)とする.このとき,任意の$j, k$に対して $$ [X_j, X_k] = \sum_{l=1}^N c_{jkl} X_l $$ となる一意的な定数$c_{jkl}$を,選んだ基底に関する$\mathfrak{g}$の構造定数と呼ぶ.
構造定数は物理学の文献で頻繁に現れるが,あまり詳しく扱わない.構造定数は次の2つの条件を満たす:すべての$j, k, l, m$について \begin{align} c_{jkl}+c_{kjl}=&0 \\ \sum_{n}(c_{jkn}c_{nlm}+c_{kln}c_{njm}+c_{ljn}c_{nkm})=&0 \end{align} 最初の条件はbracketの歪対称性から,2番目の条件はJacobi恒等式から導かれる.
さまざまな特別なタイプのLie代数について考察しよう.
単純Lie代数
Lie代数$\mathfrak{g}$が既約であるとは,$\mathfrak{g}$のイデアルが$\mathfrak{g}$自身と$\{0\}$のみである場合をいう.また,$\mathfrak{g}$が既約かつ$\dim \mathfrak{g} \geq 2$であるとき,$\mathfrak{g}$は単純Lie代数と呼ばれる.
1次元のLie代数は確かに既約である.なぜなら,非自明な部分空間を持たず,したがって非自明な部分代数やイデアルも持たないからである.しかしながら,このようなLie代数は定義により単純とはみなされない.
1次元のLie代数$\mathfrak{g}$は必ず可換であることに注意.なぜなら,任意の$X \in \mathfrak{g}$と任意のスカラー$a, b$について$[aX, bX] = 0$が成り立つからである.一方,$\mathfrak{g}$が可換であれば,$\mathfrak{g}$の任意の部分空間はイデアルとなる.したがって,可換Lie代数が既約となるのは1次元の場合のみである.このことから,「単純」の同値な定義として,「Lie代数が既約かつ非可換である場合に単純である」と言うことができる.
群とLie代数の間には類似性があり,群における部分群の役割はLie代数における部分代数が担い,正規部分群の役割はイデアルが担う(例えば,Lie代数準同型の核は常にイデアルであり,Lie群準同型の核が常に正規部分群であるのと同様である).しかし,両分野の用語には一貫性がない.群の側では,非自明な正規部分群を持たない群はすべて単純群と呼ばれ,最も明白な例は素数位数の巡回群である.一方,Lie代数の側では,非自明なイデアルを持たない最も明白な例,すなわち1次元のLie代数は単純とは呼ばれない.
単純Lie代数の例は今後多数見ることになるが,ここではひとつだけ例を挙げておく.
$\mathfrak{sl}(2, \mathbb{C})$は単純
Lie代数$\mathfrak{sl}(2, \mathbb{C})$は単純である.
交換子イデアル
$\mathfrak{g}$がLie代数であるとき,$\mathfrak{g}$の交換子イデアルは,$\mathfrak{g}$内の交換子の線型結合全体からなる空間である.すなわち,$\mathfrak{g}$の元$Z$で,ある定数$c_j$とベクトル$X_j, Y_j \in \mathfrak{g}$を用いて $$ Z = c_1[X_1,Y_1]+\cdots + c_m[X_m,Y_m] $$ の形で表せるもの全体が交換子イデアルとなる.
任意の$X, Y \in \mathfrak{g}$に対して,交換子$[X, Y]$は$\mathfrak{g}$の交換子イデアル$\left[\mathfrak{g}, \mathfrak{g}\right]$に含まれる.特に,$X$が$\left[\mathfrak{g}, \mathfrak{g}\right]$に含まれる場合も成り立つので,$\left[\mathfrak{g}, \mathfrak{g}\right]$は$\mathfrak{g}$のイデアルであることが分かる.
可解Lie代数
任意のLie代数$\mathfrak{g}$に対して,部分代数の列$\mathfrak{g}_0, \mathfrak{g}_1, \mathfrak{g}_2, \ldots$を次のように帰納的に定義する:$\mathfrak{g}_0 = \mathfrak{g}$,$\mathfrak{g}_1 = [\mathfrak{g}_0, \mathfrak{g}_0]$,$\mathfrak{g}_2 = [\mathfrak{g}_1, \mathfrak{g}_1]$,$\ldots$,これらの部分代数は$\mathfrak{g}$の導来列と呼ばれる.ある$j$で$\mathfrak{g}_j = \{0\}$となるとき,$\mathfrak{g}$は可解Lie代数と呼ばれる.
Jacobi恒等式と$j$に関する帰納法を用いることで,各$\mathfrak{g}_j$が$\mathfrak{g}$のイデアルであることは容易に示せる.
冪零Lie代数
任意のLie代数$\mathfrak{g}$に対して,イデアルの列$\mathfrak{g}_j$を次のように帰納的に定義する.まず$\mathfrak{g}_0 = \mathfrak{g}$とし,$\mathfrak{g}_{j+1}$は,$X \in \mathfrak{g}$と$Y \in \mathfrak{g}_j$に対する交換子$[X, Y]$の線型結合全体の空間とする.これらの部分代数は$\mathfrak{g}$の昇中心列と呼ばれる.ある$j$で$\mathfrak{g}_j = \{0\}$となるとき,$\mathfrak{g}$は冪零Lie代数と呼ばれる.
同値な定義として,$\mathfrak{g}_j$はすべての$j$次交換子 $$ [X_1,[X_2,[X_3,\ldots[X_j,X_{j+1}]\ldots]]] $$ の線型結合全体の空間である.すべての$j$次交換子は,$X_j$や$X_{j+1}$を適切に選ぶことで,$(j+1)$次交換子にもなり得るので,$\mathfrak{g}_{j+1} \subset \mathfrak{g}_j$が成り立つ.任意の$X \in \mathfrak{g}$と$Y \in \mathfrak{g}_j$について,$[X, Y] \in \mathfrak{g}_{j+1} \subset \mathfrak{g}_j$が成り立つので,$\mathfrak{g}_j$は$\mathfrak{g}$のイデアルであることが分かる.また,すべての$j$について$\mathfrak{g}_{j+1} \subset \mathfrak{g}_j$が成り立つので,$\mathfrak{g}$が冪零であれば,$\mathfrak{g}$は可解でもある.
上三角行列Lie代数は冪零
$\mathfrak{g}\subset M_3(\mathbb{R})$,すなわち対角成分がすべてゼロの$3 \times 3$上三角行列全体の空間とすると,$\mathfrak{g}$は冪零Lie代数である.
可解だが冪零でない
$\mathfrak{g} \subset M_2(\mathbb{C})$を,すべての$a, b, c \in \mathbb{C}$に対して $$ \begin{pmatrix} a & b \\ 0 & c \end{pmatrix} $$ の形の$2 \times 2$行列全体の空間とする.この$\mathfrak{g}$は可解Lie代数だが,冪零ではない.
各行列Lie群$G$にLie代数$\mathfrak{g}$を対応させたい.群に関する多くの問題は,Lie代数に移して線型代数の手法を使って調べることができる.まず$\mathfrak{g}$を集合として定義し,次にLie代数の構造を与える.
行列Lie代数
$G$を行列Lie群とする.$G$の行列Lie代数($\mathfrak{g}$)は,すべての実数$t$に対して$\exp(tX)$が$G$に含まれるような行列$X$全体の集合である.
同値な定義として,$X$が$\mathfrak{g}$に含まれるとは,$X$によって生成される全ての1次元部分群が$G$に含まれる場合である.単に$\exp(X)$が$G$に含まれるだけでは,$X$が$\mathfrak{g}$に属することは保証されない点に注意.$G$が$\mathrm{GL}(n, \mathbb{C})$の部分群(必ずしも$\mathrm{GL}(n, \mathbb{R})$の部分群ではない)であっても,すべての複素数$t$に対して$\exp(tX)$が$G$に含まれることは要求せず,実数$t$についてのみ$\exp(tX)$が$G$に含まれることを要求する.後で,すべての行列Lie群が$\mathrm{GL}(n, \mathbb{C})$の埋め込み部分多様体であることを示す.さらに,$\mathfrak{g}$が$G$の単位元における接空間であることも示す.
これから,行列Lie群$G$のLie代数$\mathfrak{g}$の基本的な性質をいくつか示す.特に,$\mathfrak{g}$上にbracket演算が定義でき,$\mathfrak{g}$がLie代数になることを見る.
Lie代数は単位元成分を生成する
$G$を行列Lie群,$X$をそのLie代数の元とする.このとき,$\exp(X)$は$G$の単位元成分$G_0$に含まれる.
行列Lie代数の性質
$G$を行列Lie群,$\mathfrak{g}$をそのLie代数とする.$X, Y \in \mathfrak{g}$に対して,次の性質が成り立つ:
- $AXA^{-1} \in \mathfrak{g}$(任意の$A \in G$について)
- $sX \in \mathfrak{g}$(任意の実数$s$について)
- $X + Y \in \mathfrak{g}$
- $XY - YX \in \mathfrak{g}$
この結果から,行列Lie群のLie代数は実Lie代数であり,bracket演算は$[X, Y] = XY - YX$で与えられることが分かる.$X, Y \in \mathfrak{g}$に対して,$[X, Y] = XY - YX \in \mathfrak{g}$を$X$と$Y$のbracketまたは交換子と呼ぶ.
$G$の元が複素成分を持つ場合でも,$G$のLie代数$\mathfrak{g}$が必ずしも複素ベクトル空間になるとは限らないことに注意.というのも,2番目の性質($sX \in \mathfrak{g}$)は一般には$s \in \mathbb{R}$の場合にのみ成り立つからである.ただし,場合によっては$\mathfrak{g}$が複素ベクトル空間となることもある.
複素Lie代数
行列Lie群$G$が複素Lie群であるとは,そのLie代数$\mathfrak{g}$が$M_n(\mathbb{C})$の複素部分空間,すなわち任意の$X \in \mathfrak{g}$に対して$iX \in \mathfrak{g}$が成り立つ場合をいう.
複素Lie群の例としては,$GL(n, \mathbb{C}),SL(n, \mathbb{C}),SO(n, \mathbb{C}),Sp(n, \mathbb{C})$などが挙げられる.
Lie群が可換ならLie代数も可換
$G$が可換Lie群であれば,そのLie代数$\mathfrak{g}$も可換である.
また,$G$が連結で$\mathfrak{g}$が可換なら,$G$も必ず可換となる.
物理学者は$t \mapsto e^{itX}$という写像を使うことに慣れており,$t \mapsto e^{tX}$とは異なる.したがって,物理学者が行列Lie群のLie代数について書く式は,ここで導く式と$i$の因子だけ異なることになる.
行列Lie群のLie代数
$\mathrm{GL}(n, \mathbb{C})$のLie代数は,すべての$n \times n$複素行列($M_n(\mathbb{C})$)の空間である.同様に,$\mathrm{GL}(n, \mathbb{R})$のLie代数は,すべての$n \times n$実行列($M_n(\mathbb{R})$)の空間である.$\mathrm{SL}(n, \mathbb{C})$のLie代数は,トレースがゼロのすべての$n \times n$複素行列の空間であり,$\mathrm{SL}(n, \mathbb{R})$のLie代数は,トレースがゼロのすべての$n \times n$実行列の空間である.
これらの群のLie代数は,それぞれ$\mathfrak{gl}(n, \mathbb{C})$,$\mathfrak{gl}(n, \mathbb{R})$,$\mathfrak{sl}(n, \mathbb{C})$,$\mathfrak{sl}(n, \mathbb{R})$と表記される.
行列Lie群のLie代数
$U(n)$のLie代数は,$X^\dagger = -X$を満たすすべての複素行列$X$の空間である.$SU(n)$のLie代数は,$X^\dagger = -X$かつ$\mathrm{tr}(X) = 0$を満たすすべての複素行列$X$の空間である.直交群$O(n)$のLie代数は,$X^\mathrm{tr} = -X$を満たすすべての実行列$X$の空間であり,特殊直交群$SO(n)$のLie代数は$O(n)$のLie代数と同じである.
$U(n)$と$SU(n)$のLie代数は,それぞれ$\mathfrak{u}(n)$および$\mathfrak{su}(n)$と表記される.$SO(n)$($O(n)$と同じ)のLie代数は$\mathfrak{so}(n)$と表記される.
行列Lie群のLie代数
$O(n, k)$のLie代数は,実行列$X$で $$ gX^{\mathrm{tr}}g = -X \quad g=\begin{pmatrix} I_n & 0 \\ 0 & -I_k \end{pmatrix} $$ を満たすもの全体である.$SO(n, k)$のLie代数は$O(n, k)$のLie代数と同じである.$Sp(n, \mathbb{R})$のLie代数は,実行列$X$で $$ \Omega X^{\mathrm{tr}} \Omega = X \quad \Omega=\begin{pmatrix} 0 & I \\ -I & 0 \end{pmatrix} $$ を満たすもの全体であり,$Sp(n, \mathbb{C})$のLie代数は,同じ条件を満たす複素行列$X$全体である.$Sp(n)$のLie代数は,複素行列$X$で$\Omega X^{\mathrm{tr}} \Omega = X$かつ$X^* = -X$を満たすもの全体である.
$SO(n, k)$のLie代数($O(n, k)$と同じ)は$\mathfrak{so}(n, k)$と表記され,シンプレクティック群のLie代数はそれぞれ$\mathfrak{sp}(n, \mathbb{R})$,$\mathfrak{sp}(n, \mathbb{C})$,$\mathfrak{sp}(n)$と表記される.
行列Lie群のLie代数
Heisenberg群$H$のLie代数は,次の形のすべての行列の空間である: $$ X=\begin{pmatrix} 0 & a & b \\ 0 & 0 & c \\ 0 & 0 & 0 \end{pmatrix} $$ ここで$a, b, c \in \mathbb{R}$である.
次の定理は,2つのLie群の間のLie群準同型が,対応するLie代数の間の写像を自然に誘導することを述べている.この結果から,同型なLie群は同型なLie代数を持つことが分かる.
Lie群準同型はLie代数準同型を誘導
$G$と$H$を行列Lie群とし,それぞれのLie代数を$\mathfrak{g}$と$\mathfrak{h}$とする.$\Phi: G \to H$がLie群準同型であるとき,$\mathfrak{g}$から$\mathfrak{h}$への一意な実線型写像$\phi$が存在し, $$ \Phi(e^X) = e^{\phi(X)} $$ がすべての$X \in \mathfrak{g}$について成り立つ.この写像$\phi$は次の性質を持つ:
- すべての$X \in \mathfrak{g}$,$A \in G$について$\phi(AXA^{-1}) = \Phi(A)\phi(X)\Phi(A)^{-1}$
- すべての$X, Y \in \mathfrak{g}$について$\phi([X, Y]) = [\phi(X), \phi(Y)]$
- すべての$X \in \mathfrak{g}$について$\phi(X) = \frac{d}{dt}\Phi(e^{tX})\bigg|_{t=0}$
実際には,Lie群準同型$\Phi$が与えられたとき,$\phi$を計算する方法は主に性質3を使う.多様体の言葉で言えば,性質3は$\phi$が$\Phi$の単位元における微分(または導関数)であることを意味する.性質2より,$\phi: \mathfrak{g} \to \mathfrak{h}$はLie代数準同型となる.したがって,すべてのLie群準同型はLie代数準同型を誘導する.後で逆の問題,すなわちLie群のLie代数間の準同型$\phi$が与えられたとき,それに対応するLie群準同型$\Phi$が存在するかどうかを述べる.
Lie群準同型の合成はLie代数準同型の合成を誘導
$G, H, K$を行列Lie群とし,$\Phi: H \to K$および$\Psi: G \to H$をLie群準同型とする.$\Lambda: G \to K$を$\Phi$と$\Psi$の合成とし,$\lambda, \phi, \psi$をそれぞれ$\Phi, \Psi, \varphi$に対応するLie代数写像とする.このとき, $$ \lambda = \phi \circ \psi $$ が成り立つ.
Lie群準同型の核はLie代数準同型の核
$\Phi: G \to H$がLie群準同型であり,$\phi: \mathfrak{g} \to \mathfrak{h}$が対応するLie代数準同型であるとする.このとき,$\Phi$の核は$G$の閉じた正規部分群であり,そのLie代数は $$ \mathrm{Lie}(\ker (\Phi)) = \ker (\phi) $$ で与えられる.
随伴写像
$G$を行列Lie群,$\mathfrak{g}$をそのLie代数とする.各$A \in G$に対して,線型写像$\mathrm{Ad}_A: \mathfrak{g} \to \mathfrak{g}$を $$ \mathrm{Ad}_A(X) = AXA^{-1} $$ により定義する.
随伴写像の性質
$G$を行列Lie群,$\mathfrak{g}$をそのLie代数とする.$\mathrm{GL}(\mathfrak{g})$を$\mathfrak{g}$上のすべての可逆線型変換の群とする.このとき,$A \mapsto \mathrm{Ad}_A$は$G$から$\mathrm{GL}(\mathfrak{g})$への群準同型である.さらに,任意の$A \in G$に対して,$\mathrm{Ad}_A$はすべての$X, Y \in \mathfrak{g}$について $$ \mathrm{Ad}_A([X, Y]) = [\mathrm{Ad}_A(X), \mathrm{Ad}_A(Y)] $$ を満たす.
$\mathfrak{g}$が$k$次元の実ベクトル空間であるため,$\mathrm{GL}(\mathfrak{g})$は本質的に$\mathrm{GL}(k, \mathbb{R})$と同じである.したがって,$\mathrm{GL}(\mathfrak{g})$を行列Lie群とみなす.$\mathrm{Ad}: G \to \mathrm{GL}(\mathfrak{g})$は連続であり,Lie群準同型であることは容易に示せる.定理3.28より,$G$のLie代数$\mathfrak{g}$から$\mathrm{GL}(\mathfrak{g})$のLie代数$\mathfrak{gl}(\mathfrak{g})$への対応する実線型写像$X \mapsto \mathrm{ad}_X$が存在し,次の性質を持つ: $$ e^{\mathrm{ad}_X} = \mathrm{Ad}_{e^X} $$ ここで,$\mathrm{gl}(\mathfrak{g})$は$\mathrm{GL}(\mathfrak{g})$のLie代数,すなわち$\mathfrak{g}$から$\mathfrak{g}$へのすべての線型写像の空間である.
随伴写像の性質
$G$を行列Lie群,$\mathfrak{g}$をそのLie代数とする.$\mathrm{Ad}: G \to \mathrm{GL}(\mathfrak{g})$を定義し,$\mathrm{ad}: \mathfrak{g} \to \mathfrak{gl}(\mathfrak{g})$を対応するLie代数写像とする.このとき,すべての$X, Y \in \mathfrak{g}$について $$ \mathrm{ad}_X(Y) = [X, Y] $$
この命題は,$\mathrm{ad}_X$という記法が,前の記法と一致していることを示している.
結果として,次の事実が証明できる.この結果は後で利用する.
Baker-Campbell-Hausdorffの公式
任意の$X \in M_n(\mathbb{C})$に対して,$\mathrm{ad}_X: M_n(\mathbb{C}) \to M_n(\mathbb{C})$を$\mathrm{ad}_X(Y) = [X, Y]$で定義する.このとき,任意の$Y \in M_n(\mathbb{C})$について $$ e^X Y e^{-X} = \mathrm{Ad}_{e^X}(Y) = e^{\mathrm{ad}_X}(Y) $$ ここで $$ e^{\mathrm{ad}_X}(Y) = Y + [X, Y] + \frac{1}{2}[X, [X, Y]] + \cdots $$
行列Lie群$G$の表現を調べる際(後で扱う),しばしば$G$のLie代数$\mathfrak{g}$に移ることが有用である.$\mathfrak{g}$は一般には実Lie代数であるが,さらに関連する複素Lie代数,すなわち$\mathfrak{g}$の複素化に移ることが有用な場合も多い.
複素化
$V$が有限次元の実ベクトル空間であるとき,$V$の複素化($V_\mathbb{C}$)は,$V$の元$v_1, v_2$を用いて $$ v_1 + i v_2 $$ の形の形式的な線型結合全体の空間である.これは明らかに実ベクトル空間となり,さらに $$ i(v_1 + i v_2) = -v_2 + i v_1 $$ のように複素数の作用を定めることで,複素ベクトル空間にもなる.
より厳密には,$V_\mathbb{C}$を$V$の元$v_1, v_2$からなる順序対$(v_1, v_2)$全体の空間と定義することもできるが,この記法は煩雑である.上記の定義で$V_\mathbb{C}$が複素ベクトル空間になることは容易に確かめられる.$V$は明らかに$V_\mathbb{C}$の実部分空間として埋め込まれる.
Lie代数の複素化
$\mathfrak{g}$を有限次元の実Lie代数,$\mathfrak{g}_\mathbb{C}$をその複素化とする.このとき,$\mathfrak{g}$上のbracket演算は,$\mathfrak{g}_\mathbb{C}$上への一意な拡張を持ち,$\mathfrak{g}_\mathbb{C}$を複素Lie代数にする.この複素Lie代数$\mathfrak{g}_\mathbb{C}$を,実Lie代数$\mathfrak{g}$の複素化と呼ぶ.
複素化と行列Lie代数の同型
$\mathfrak{g} \subset M_n(\mathbb{C})$が実Lie代数であり,すべての非零$X \in \mathfrak{g}$について$iX \notin \mathfrak{g}$とする.このとき,「抽象的な」複素化$\mathfrak{g}_\mathbb{C}$は,$\mathfrak{g}$の元$X, Y$を用いて$X + iY$の形で表される$M_n(\mathbb{C})$内の行列全体の集合と同型である.
この命題から,次の同型の一覧が容易に得られる: \begin{align} \mathfrak{gl}(n, \mathbb{R})_\mathbb{C} &\cong \mathfrak{gl}(n,\mathbb{C}) \\ \mathfrak{u}(n)_{\mathbb{C}} &\cong \mathfrak{gl}(n, \mathbb{C}) \\ \mathfrak{su}(n)_{\mathbb{C}} &\cong \mathfrak{sl}(n, \mathbb{C}) \\ \mathfrak{sl}(n, \mathbb{R})_{\mathbb{C}} &\cong \mathfrak{sl}(n, \mathbb{C}) \\ \mathfrak{so}(n)_{\mathbb{C}} &\cong \mathfrak{so}(n, \mathbb{C}) \\ \mathfrak{sp}(n, \mathbb{R})_{\mathbb{C}} &\cong \mathfrak{sp}(n, \mathbb{C}) \\ \mathfrak{sp}(n)_{\mathbb{C}} &\cong \mathfrak{sp}(n, \mathbb{C}) \end{align}
$\mathfrak{su}(2)_{\mathbb{C}}$と$\mathfrak{sl}(2, \mathbb{R})_{\mathbb{C}}$はいずれも$\mathfrak{sl}(2, \mathbb{C})$と同型であるが,$\mathfrak{su}(2)$と$\mathfrak{sl}(2, \mathbb{R})$自体は同型ではない.
複素化と準同型の拡張
$\mathfrak{g}$を実Lie代数,$\mathfrak{g}_\mathbb{C}$をその複素化,$\mathfrak{h}$を任意の複素Lie代数とする.このとき,$\mathfrak{g}$から$\mathfrak{h}$への任意の実Lie代数準同型は,$\mathfrak{g}_\mathbb{C}$から$\mathfrak{h}$への複素Lie代数準同型へ一意的に拡張できる.
この結果は,実Lie代数の複素化に関する普遍性の性質(universal property)である.
指数写像
$G$が行列Lie群でLie代数を$\mathfrak{g}$とするとき,指数写像は $$ \exp: \mathfrak{g} \to G $$ という写像である.
すなわち,$G$の指数写像は,$G$のLie代数$\mathfrak{g}$に制限された行列指数関数である.$\mathrm{GL}(n, \mathbb{C})$の任意の行列は,ある$n \times n$行列の指数関数として表せる.しかし,$G \subset \mathrm{GL}(n, \mathbb{C})$が閉部分群である場合,$G$の元$A$で,$G$のLie代数$\mathfrak{g}$の元$X$が存在して$\exp(X) = A$となるものが存在しない場合もある.
したがって,行列Lie群$G$の指数写像は,Lie代数$\mathfrak{g}$全体を$G$に写すとは限らない.また,指数写像は$\mathfrak{g}$上で一対一とは限らない(例えば$\mathfrak{g} = \mathfrak{su}(2)$の場合がそうである).それでも,指数写像は群とLie代数の間で情報をやり取りする重要な手段となる.実際,後で指数写像が局所的には一対一かつ全射であることを示す.この事実は後で本質的に利用される.
指数写像の性質
$0 < \epsilon < \log 2$とするとき,$U_\epsilon = \{ X \in M_n(\mathbb{C}) \mid \|X\| < \epsilon \}$,$V_\epsilon = \exp(U_\epsilon)$と定める.$G \subset \mathrm{GL}(n, \mathbb{C})$を行列Lie群,$\mathfrak{g}$をそのLie代数とする.このとき,$\epsilon \in (0, \log 2)$が存在して,すべての$A \in V_\epsilon$について,$A \in G$であることと$\log A \in \mathfrak{g}$であることは同値である.
「$\epsilon < \log 2$」という条件は,すべての$X \in U_\epsilon$について$\log(e^X)$が定義され,$X$に等しいことを保証する.$X = \log A$が$\mathfrak{g}$に含まれていれば,$A = e^X$は$G$に含まれることに注意.したがって,この定理の内容は,ある$\epsilon$に対して$A \in V_\epsilon \cap G$であれば,$\log A$が$\mathfrak{g}$に含まれることを意味する.
「指数写像の性質」の系1
$G$が行列Lie群でLie代数を$\mathfrak{g}$とするとき,$\mathfrak{g}$の$0$の近傍$U$と$G$の単位元$I$の近傍$V$が存在し,指数写像$\exp$は$U$を$V$へと同相写像として写す.
「指数写像の性質」の系2
$G$を行列Lie群,$\mathfrak{g}$をそのLie代数,$k$を$\mathfrak{g}$の実ベクトル空間としての次元とする.このとき,$G$は$M_n(\mathbb{C})$内の滑らかな埋め込み部分多様体であり,その次元は$k$である.したがって,$G$はLie群となる.
この系から,$G$は局所的に弧状連続であることが従う.すなわち,$G$の任意の点には,$\mathbb{R}^k$のボールと同相な近傍$U$が存在し,したがって$U$は道連続である.したがって,$G$が連結(通常の位相的意味で)であることと,弧状連続であることは同値である.
「指数写像の性質」の系3
$G \subset \mathrm{GL}(n, \mathbb{C})$が行列Lie群でLie代数を$\mathfrak{g}$とする.ある行列$X$が$\mathfrak{g}$に含まれることと,$M_n(\mathbb{C})$内の滑らかな曲線$\gamma$が存在して,すべての$t$について$\gamma(t) \in G$,$\gamma(0) = I$,および$\frac{d\gamma}{dt}\bigg|_{t=0} = X$となることは同値である.したがって,$\mathfrak{g}$は$G$の単位元における接空間である.
「指数写像の性質」の系4
$G$が連結な行列Lie群であれば,$G$の任意の元$A$は $$ A = e^{X_1} e^{X_2} \cdots e^{X_m} $$ の形に書ける.ここで,$X_1, X_2, \ldots, X_m$はすべて$\mathfrak{g}$の元である.
$G$が連結であっても,一般には任意の$A \in G$を単一の指数関数,すなわち$A = \exp(X)$($X \in \mathfrak{g}$)の形で書くことはできない.
「指数写像の性質」の系5
$G$と$H$を行列Lie群とし,それぞれのLie代数を$\mathfrak{g}$と$\mathfrak{h}$とする.$G$が連結であると仮定する.$\hat{1}$と$\hat{2}$を$G$から$H$へのLie群準同型とし,$\phi_1$と$\phi_2$をそれぞれ$\mathfrak{g}$から$\mathfrak{h}$への対応するLie代数準同型とする.もし$\phi_1 = \phi_2$ならば,$\hat{1} = \hat{2}$が成り立つ.
「指数写像の性質」の系6
2つの行列Lie群の間の任意の連続な準同型写像は滑らか(微分可能)である.
「指数写像の性質」の系7
$G$が連結な行列Lie群であり,そのLie代数$\mathfrak{g}$が可換であれば,$G$も可換である.
「指数写像の性質」の系8
$G \subset M_n(\mathbb{C})$が行列Lie群であるとき,$G$の単位元成分$G_0$は$\mathrm{GL}(n, \mathbb{C})$の閉部分群であり,したがって行列Lie群となる.さらに,$G_0$のLie代数は$G$のLie代数と同じである.
表現論
$V$が有限次元の実または複素ベクトル空間であるとき,$\mathrm{GL}(V)$は$V$上の可逆線型変換全体の群である.$V$の基底を選べば,$\mathrm{GL}(V)$を$\mathrm{GL}(n, \mathbb{R})$または$\mathrm{GL}(n, \mathbb{C})$と同一視できる.このような同一視によって$\mathrm{GL}(V)$に位相が入るが,これは基底の選び方によらず同じになる.この議論を踏まえ,$\mathrm{GL}(V)$を行列Lie群とみなす.同様に,$\mathfrak{gl}(V) = \mathrm{End}(V)$は$V$から$V$へのすべての線型写像の空間であり,括弧演算$[X, Y] = XY - YX$によってLie代数となる.
Lie群の表現
$G$を行列Lie群とする.$G$の有限次元複素表現とは,有限次元複素ベクトル空間$V$($\dim V \geq 1$)に対するLie群準同型 $$ \Pi: G \to \mathrm{GL}(V) $$ である.$G$の有限次元実表現とは,有限次元実ベクトル空間$V$に対するLie群準同型 $$ \Pi: G \to \mathrm{GL}(V) $$ である.
Lie代数の表現
$\mathfrak{g}$が実または複素Lie代数であるとき,$\mathfrak{g}$の有限次元複素表現とは,有限次元複素ベクトル空間$V$に対するLie代数準同型 $$ \pi: \mathfrak{g} \to \mathfrak{gl}(V) $$ である.$\mathfrak{g}$が実Lie代数である場合,$\mathfrak{g}$の有限次元実表現とは,有限次元実ベクトル空間$V$に対するLie代数準同型 $$ \pi: \mathfrak{g} \to \mathfrak{gl}(V) $$ である.
忠実な表現
表現が全単射である場合,その表現は忠実な表現と呼ばれる.
表現とは,群やLie代数がベクトル空間上で線型に作用するものと考えるべきである(例えば,各$g \in G$に対して,ベクトル空間$V$上で作用する演算子$\pi(g)$が対応する).準同型$\pi: G \to \mathrm{GL}(V)$が固定されている場合,しばしば $$ g \cdot v $$ という記法を$\pi(g)v$の代わりに用いることがある.「$G$が空間$V$上に作用する表現$\pi$」のような言い方もよく使う.
ある表現が行列Lie群$G$の忠実な表現である場合,$\{\Pi(A) \mid A \in G\}$は元の群$G$と同型な行列群となる.したがって,$\Pi$によって$G$を行列群として表すことができる.これが「表現」という用語の動機である(もちろん,忠実でなくても「表現」と呼ぶ).ただし,用語の由来とは異なり,表現論の目的は単に群を行列群として表すことではない.そもそも本書で扱う群はすでに行列群である.むしろ,表現論の目的は,固定した群が行列群として作用するすべての方法(同型を除く)を分類することである.
群の線型作用は数学や物理の多くの分野で自然に現れる.典型的な例は,3次元空間における回転対称性を持つ線型微分方程式であり,例えば量子力学の水素原子のエネルギー状態を記述する方程式がそうである.方程式が回転不変であるため,解空間も回転によって不変となり,したがって回転群 $SO(3)$ の表現となる.$SO(3)$(またはその Lie 代数)の表現論は,解空間がどのようなものになり得るかを絞り込むのに非常に役立つ.
既約表現
$V$が有限次元の実または複素ベクトル空間であり,$G$が行列Lie群であるとき,$G$の表現が$V$上に作用するとする.$V$の部分空間$W$が不変部分空間であるとは,すべての$w \in W$とすべての$A \in G$について,$\Pi(A) w \in W$が成り立つ場合をいう.不変部分空間$W$が非自明であるとは,$W \neq \{0\}$かつ$W \neq V$である場合をいう.非自明な不変部分空間を持たない表現は既約と呼ばれる.
不変,非自明,既約という用語は,Lie代数の表現についても同様に定義される.
$\mathfrak{g}$が実Lie代数であっても,主に$\mathfrak{g}$の複素表現を考察する.ここで強調しておきたいのは,実Lie代数$\mathfrak{g}$が複素ベクトル空間$V$上に作用する複素表現について述べる場合,不変部分空間$W$は$V$の複素部分空間でなければならない,ということである.
絡写像
$G$を行列Lie群とし,$\Pi$を$G$の表現($V$上に作用),$\Sigma$を$G$の表現($W$上に作用)とする.線型写像$\phi: V \to W$が絡写像であるとは,すべての$A \in G$とすべての$v \in V$について $$ \phi(\Pi(A)v) = \Sigma(A)\phi(v) $$ が成り立つ場合をいう.
Lie代数の表現についても同様に絡写像が定義される.
表現の同型
$\phi$が表現の絡写像であり,さらに$\phi$が可逆(逆写像を持つ)である場合,$\phi$は表現の同型写像と呼ばれる.$V$と$W$の間に同型写像が存在する場合,それらの表現は同型であると言う.
「作用」記法を用いると,絡写像の定義的性質は次のように書ける: $$ \phi(A \cdot v) = A \cdot \phi(v) $$ すべての $A \in G$ および $v \in V$ について成り立つ.すなわち,$\phi$ は $G$ の作用と可換でなければならない. 表現論の典型的な問題は,ある群やLie代数の既約表現を同型を除いてすべて分類することである.後に,Lie代数 $\mathfrak{sl}(2, \mathbb{C})$ の有限次元複素既約表現をすべて決定する.
$\mathrm{GL}(V)$を$\mathrm{GL}(n, \mathbb{R})$または$\mathrm{GL}(n, \mathbb{C})$と同一視した後,次の系が得られる.
行列Lie群の表現とLie代数の表現
$G$を行列Lie群,そのLie代数を$\mathfrak{g}$,$G$の(有限次元の実または複素)表現を$V$上に作用するものとする.このとき,同じ空間$V$上に一意な$\mathfrak{g}$の表現$\pi$が存在し, $$ \Pi(e^X) = e^{\pi(X)} $$ がすべての$X \in \mathfrak{g}$について成り立つ.$\pi$は $$ \pi(X) = \frac{d}{dt}\Pi(e^{tX})\bigg|_{t=0} $$ で計算でき,さらにすべての$X \in \mathfrak{g}$,$A \in G$について $$ \pi(AXA^{-1}) = \Pi(A)\pi(X)\Pi(A)^{-1} $$ が成り立つ.
行列Lie群$G$とそのLie代数$\mathfrak{g}$が与えられたとき,$\mathfrak{g}$の任意の表現$\pi$が$G$の表現$\Pi$から来るかどうかを問うことができる.実際には,これは一般には成り立たないが,$G$が単連結であれば成り立つ.
行列Lie群の表現とLie代数の表現の性質
- $G$を連結な行列Lie群,そのLie代数を$\mathfrak{g}$とする.$G$の表現$\Pi$と対応するLie代数の表現$\pi$について,$\Pi$が既約であることと$\pi$が既約であることは同値である.
- $G$を連結な行列Lie群とし,$G$の表現$\Pi_1, \Pi_2$と対応するLie代数の表現$\pi_1, \pi_2$について,$\pi_1$と$\pi_2$が同型であることと$\Pi_1$と$\Pi_2$が同型であることは同値である.
複素化と表現
$\mathfrak{g}$を実Lie代数,$\mathfrak{g}_\mathbb{C}$をその複素化とする.このとき,$\mathfrak{g}$の任意の有限次元複素表現$\pi$は,$\mathfrak{g}_\mathbb{C}$への複素線型表現へ一意的に拡張でき,この拡張も$\pi$と表す.さらに,$\pi$が$\mathfrak{g}_\mathbb{C}$の表現として既約であることと,$\mathfrak{g}$の表現として既約であることは同値である.
もちろん,$\mathfrak{g}_\mathbb{C}$への拡張は,$X + iY$ に対して $\varphi(X + iY) = \varphi(X) + i\varphi(Y)$ で与えられる($X, Y \in \mathfrak{g}$).
ユニタリ表現
$V$が有限次元の内積空間であり,$G$が行列Lie群であるとき,表現$\Pi: G \to \mathrm{GL}(V)$がユニタリ表現であるとは,すべての$A \in G$について$\Pi(A)$が$V$上のユニタリ作用素となる場合をいう.
ユニタリ表現の性質
$G$を行列Lie群,Lie代数を$\mathfrak{g}$とする.$V$を有限次元の内積空間とし,$\Pi$を$G$の表現($V$上に作用),$\pi$を対応するLie代数の表現とする.$\Pi$がユニタリ表現であれば,すべての$X \in \mathfrak{g}$について$\pi(X)$は歪自己共役作用素となる.逆に,$G$が連結であり,すべての$X \in \mathfrak{g}$について$\pi(X)$が歪自己共役作用素であれば,$\Pi$はユニタリ表現となる.
若干の記法の濫用だが,有限次元内積空間上で実Lie代数$\mathfrak{g}$が表現$\pi$として作用するとき,すべての$X \in \mathfrak{g}$について$\pi(X)$が歪自己共役作用素であれば,その表現はユニタリであると言うことにする.
標準表現
行列Lie群$G$は定義により,ある$\mathrm{GL}(n, \mathbb{C})$の部分集合である.$G$から$\mathrm{GL}(n, \mathbb{C})$への包含写像(すなわち$\Pi(A) \mapsto A$)は,$G$の標準表現と呼ばれる表現である.$G$が$\mathrm{GL}(n, \mathbb{R}) \subset \mathrm{GL}(n, \mathbb{C})$に含まれている場合,標準表現を実表現として考えることもできる.同様に,$\mathfrak{g} \subset M_n(\mathbb{C})$が行列Lie代数である場合,$\varphi(X) = X$という写像は$\mathfrak{g}$の標準表現と呼ばれる.
例えば,$\mathrm{SO}(3)$の標準表現は,$\mathrm{SO}(3)$が通常の方法で$\mathbb{R}^3$上に作用する表現であり,$\mathrm{SU}(2)$の標準表現は,$\mathrm{SU}(2)$が通常の方法で$\mathbb{C}^2$上に作用する表現である.
自明表現
1次元複素ベクトル空間$\mathbb{C}$を考える.任意の行列Lie群$G$に対して,自明表現を $$ \Pi(A) = I $$ (すべての$A \in G$について)で定義できる.もちろん,$\mathbb{C}$は非自明な部分空間を持たないので,この表現は既約である.同様に,Lie代数$\mathfrak{g}$に対しても, $$ \pi(X) = 0 $$ (すべての$X \in \mathfrak{g}$について)で自明表現を定義できる.これも既約表現である.
随伴表現
$G$が行列Lie群でLie代数を$\mathfrak{g}$とするとき,$G$の随伴表現は,$G$から$\mathrm{GL}(\mathfrak{g})$への写像 $$ \mathrm{Ad}: G \to \mathrm{GL}(\mathfrak{g}), \quad A \mapsto \mathrm{Ad}_A $$ で定義される.同様に,有限次元Lie代数$\mathfrak{g}$の随伴表現は,$\mathfrak{g}$から$\mathfrak{gl}(\mathfrak{g})$への写像 $$ \mathrm{ad}: \mathfrak{g} \to \mathfrak{gl}(\mathfrak{g}), \quad X \mapsto \mathrm{ad}_X $$ で定義される.
$G$が行列Lie群でLie代数を$\mathfrak{g}$とするとき,$G$の随伴表現に対応するLie代数表現は$\mathfrak{g}$の随伴表現となる.特に,$SO(3)$の場合,標準表現と随伴表現はいずれも3次元の実表現であり,実際これら2つの表現は同型である.
既知の表現から新しい表現を構成する方法のひとつは,いくつかの表現を組み合わせることである.ここでは,表現から新しい表現を得る標準的な3つの方法,すなわち表現の直和,表現のテンソル積,双対表現を定義する.
表現の直和
$G$を行列Lie群とし,$\Pi_1, \Pi_2, \ldots, \Pi_m$を$G$の表現(それぞれ$V_1, V_2, \ldots, V_m$上に作用)とする.このとき,$\Pi_1, \Pi_2, \ldots, \Pi_m$の直和は,$V_1 \oplus \cdots \oplus V_m$上に作用する表現 $$ [\Pi_1 \oplus \cdots \oplus \Pi_m(A)](v_1, \ldots, v_m) = (\Pi_1(A)v_1, \ldots, \Pi_m(A)v_m) $$ (すべての$A \in G$について)で定義される.同様に,$\mathfrak{g}$をLie代数とし,$\pi_1, \pi_2, \ldots, \pi_m$を$\mathfrak{g}$の表現(それぞれ$V_1, V_2, \ldots, V_m$上に作用)とするとき,$\pi_1, \pi_2, \ldots, \pi_m$の直和は,$V_1 \oplus \cdots \oplus V_m$上に作用する表現 $$ [\pi_1 \oplus \cdots \oplus \pi_m(X)](v_1, \ldots, v_m) = (\pi_1(X)v_1, \ldots, \pi_m(X)v_m) $$ (すべての$X \in \mathfrak{g}$について)で定義される.
$U$と$V$を有限次元の実または複素ベクトル空間とする.$U$と$V$から「構成される」新しいベクトル空間$U \otimes V$として,テンソル積を定義したい.まずその考え方を説明し,次に厳密な定義を与える.
要素 $u \in U$ と $v \in V$ の「積」を形式的に $u \otimes v$ と書いて考えたい.空間 $U \otimes V$ は,このような積の線型結合全体,すなわち $$ a_1 u_1 \otimes v_1 + a_2 u_2 \otimes v_2 + \cdots + a_n u_n \otimes v_n $$ の形の要素からなる空間である.「$\otimes$」を積として解釈するなら,双線型性を満たすべきである: \begin{align} (u_1 + a u_2) \otimes v =& u_1 \otimes v + a u_2 \otimes v \\ u \otimes (v_1 + a v_2) =& u \otimes v_1 + a u \otimes v_2 \end{align} 積が可換であるとは限らないことに注意.すなわち,たとえ $U = V$ で $U \otimes V$ と $V \otimes U$ が同じ空間でも,$u \otimes v$ は一般に $v \otimes u$ とは一致しない.
さて,$U$の基底を$e_1, e_2, \ldots, e_n$,$V$の基底を$f_1, f_2, \ldots, f_m$とすると,双線型性から,任意の要素は$e_j \otimes f_k$の線型結合として書けることが容易に分かる.実際,$\{e_j \otimes f_k \mid 1 \leq j \leq n, 1 \leq k \leq m\}$が$U \otimes V$の基底になると期待するのは自然である.そして,これは実際に成り立つ.
テンソル積
$U$と$V$が有限次元の実または複素ベクトル空間であるとき,$U$と$V$のテンソル積とは,ベクトル空間$W$と双線型写像 $\phi:U \times V \to W$ であって,次の性質を満たすものである:$U \times V$ からベクトル空間 $X$ への任意の双線型写像 $\psi$ に対し,$W$ から $X$ への一意な線型写像 $\bar{\psi}$ が存在して,次の図式が可換になる: $$ \begin{CD} U \times V @>{\phi}>> W \\ @V{\psi}VV @VVV \\ X @<{\bar{\psi}}<< \end{CD} $$
$U \times V$ から $X$ への双線型写像は,$W$ から $X$ への線型写像 $\bar{\psi}$ へと変換されることに注意.この点がテンソル積の重要な特徴のひとつである:$U \times V$ 上の双線型写像は,$W$ 上の線型写像へと対応する.
テンソル積の自然同型
$U$と$V$が任意の有限次元の実または複素ベクトル空間であれば,テンソル積$(W, \phi)$が存在する.さらに,$(W, \phi)$は標準的な同型を除いて一意である.すなわち,$(W_1, \phi_1)$と$(W_2, \phi_2)$が2つのテンソル積であれば,次の可換図式を満たす一意なベクトル空間の同型写像$\hat{\Phi}: W_1 \to W_2$が存在する: $$ \begin{CD} U \times V @>{\phi_1}>> W_1 \\ @V{\phi_2}VV @VVV \\ X @<{\bar{\Phi}}<< \end{CD} $$ また,$(W, \phi)$がテンソル積であり,$U$の基底を$e_1, e_2, \ldots, e_n$,$V$の基底を$f_1, f_2, \ldots, f_m$とすると, $$ \{\phi(e_j, f_k) \mid 1 \leq j \leq n, 1 \leq k \leq m\} $$ は$W$の基底となる.
特に,$\dim(U \otimes V) = (\dim U) \cdot (\dim V)$ である.
テンソル積 $U \otimes V$ は本質的に一意であるため,$U \otimes V$ で任意のテンソル積空間を表すことにし,$\phi(u, v)$ の代わりに $u \otimes v$ と書くことにする.この記法では, $$ \{e_j \otimes f_k \mid 1 \leq j \leq n, 1 \leq k \leq m\} $$ が $U \otimes V$ の基底になることを述べている(期待通りである).
$U \otimes V$ の定義的性質は「テンソル積の普遍性」と呼ばれる.この性質の重要性を理解するために,$U \otimes V$ から他の空間への線型写像 $T$ を定義したいとしよう.$U$ と $V$ の基底を使って $T$ を定義することもできるが,その場合 $T$ が基底の選び方に依存しないかどうかを気にする必要がある.あるいは,$U$ の元 $u$ と $V$ の元 $v$ からなる $u \otimes v$ の形の要素に対して $T$ を定義しようとすることもできる.上の定理より,この形の要素は $U \otimes V$ を張るが,$U \otimes V$ の任意の要素を $u \otimes v$ の線型結合として書く方法は一意ではない.したがって,この形の要素に対して $T$ を定義する場合,$T$ がwell-definedかどうかを注意深く確認する必要がある.
ここで「普遍性」の性質が本質的に効いてくる.もし $(u, v)$ に関する任意の双線型表現 $\psi(u, v)$ が与えられたとき,普遍性の性質は,$U \otimes V$ 上に一意な線型写像 $T$ が存在して $$ T(u \otimes v) = \psi(u, v) $$ となることを保証する.したがって,$u \otimes v$ の形の要素に対して $T(u \otimes v)$ の定義が $u$ と $v$ に関して双線型であれば,$U \otimes V$ 上にwell-definedな線型写像 $T$ を構成できる.次の結果はこの考え方の応用である.
テンソル積間の線形作用素
$U$と$V$を有限次元の実または複素ベクトル空間とする.$A: U \to U$および$B: V \to V$を線型作用素とする.このとき,$U \otimes V$から$U \otimes V$への一意な線型作用素$A \otimes B$が存在し, $$ (A \otimes B)(u \otimes v) = (Au) \otimes (Bv) $$ がすべての$u \in U$および$v \in V$について成り立つ.$A_1, A_2$が$U$上の線型作用素,$B_1, B_2$が$V$上の線型作用素であるとき, $$ (A_1\otimes B_1)(A_2 \otimes B_2) = (A_1 A_2) \otimes (B_1 B_2) $$ が成り立つ.
ここで表現のテンソル積を定義する準備が整った.この定義には2つの重要なアプローチがある.1つ目の方法は,群$G$が空間$U$上に作用する表現と,別の群$H$が空間$V$上に作用する表現から,積$G \times H$が空間$U \otimes V$上に作用する表現を構成するものである.2つ目の方法は,同じ群$G$の2つの異なる表現($U$上と$V$上)から,$G$が$U \otimes V$上に作用する表現を構成するものである.これら2つの方法はいずれもLie代数にも応用できる.
表現のテンソル積
$G$と$H$を行列Lie群とする.$\Pi_1$を$G$の表現($U$上に作用),$\Pi_2$を$H$の表現($V$上に作用)とする.このとき,$\Pi_1$と$\Pi_2$のテンソル積は,$G \times H$が$U \otimes V$上に作用する表現$\Pi_1 \otimes \Pi_2$であり,すべての$A \in G$,$B \in H$について $$ (\Pi_1 \otimes \Pi_2)(A, B) = \Pi_1(A) \otimes \Pi_2(B) $$ で定義される.
上の定理を用いると,$\Pi_1 \otimes \Pi_2$が実際に$G \times H$の表現になっていることは容易に確かめられる.
さて,$G$と$H$が行列Lie群(すなわち$G$が$\mathrm{GL}(n, \mathbb{C})$の閉部分群,$H$が$\mathrm{GL}(m, \mathbb{C})$の閉部分群)であれば,$G \times H$も明らかに$\mathrm{GL}(n + m, \mathbb{C})$の閉部分群として考えることができる.したがって,行列Lie群の直積も行列Lie群となる.$G \times H$のLie代数は,$G$のLie代数と$H$のLie代数の直和と同型であることは容易に確かめられる.
表現のテンソル積とLie代数
$G$と$H$を行列Lie群とし,それぞれのLie代数を$\mathfrak{g}$と$\mathfrak{h}$とする.$\Pi_1$を$G$の表現,$\Pi_2$を$H$の表現とし,$G \times H$の表現$\Pi_1 \otimes \Pi_2$を考える.対応するLie代数の表現$\pi_1 \otimes \pi_2$については,すべての$X \in \mathfrak{g}$,$Y \in \mathfrak{h}$について $$ (\pi_1 \otimes \pi_2)(X, Y) = \pi_1(X) \otimes I + I \otimes \pi_2(Y) $$ となる.
この命題から次の定義が動機付けられる.
Lie代数のテンソル積表現
$\mathfrak{g}$と$\mathfrak{h}$をLie代数とし,$\pi_1$と$\pi_2$をそれぞれ$\mathfrak{g}$と$\mathfrak{h}$の表現($U$と$V$上に作用)とする.このとき,$\pi_1$と$\pi_2$のテンソル積表現$\pi_1 \otimes \pi_2$は,$\mathfrak{g} \oplus \mathfrak{h}$が$U \otimes V$上に作用する表現であり,すべての$X \in \mathfrak{g}$,$Y \in \mathfrak{h}$について $$ (\pi_1 \otimes \pi_2)(X, Y) = \pi_1(X) \otimes I + I \otimes \pi_2(Y) $$ で定義される.
これは確かに $\mathfrak{g} \oplus \mathfrak{h}$ の表現を定義していることは容易に確かめられる.なお,もし $(\pi_1 \otimes \pi_2)(X, Y) = \pi_1(X) \otimes \pi_2(Y)$ と定義した場合,この式は $(X, Y)$ に関して線型ではないため,$\mathfrak{g} \oplus \mathfrak{h}$ の表現にはならないことに注意.
次に,先ほどの定義の変種を導入する.これは,同じ群 $G$ の2つの表現のテンソル積を取り,その結果を $G \times G$ ではなく $G$ の表現として扱うものである.
同じ群の表現のテンソル積
$G$を行列Lie群とし,$\Pi_1$と$\Pi_2$を$G$の表現(それぞれ$V_1$と$V_2$上に作用)とする.このとき,$G$のテンソル積表現は,$V_1 \otimes V_2$上に作用する表現であり,すべての$A \in G$について $$ (\Pi_1 \otimes \Pi_2)(A) = \Pi_1(A) \otimes \Pi_2(A) $$ で定義される.同様に,$\pi_1$と$\pi_2$がLie代数$\mathfrak{g}$の表現であるとき,$\mathfrak{g}$のテンソル積表現は$V_1 \otimes V_2$上に作用し,すべての$X \in \mathfrak{g}$について $$ (\pi_1 \otimes \pi_2)(X) = \pi_1(X) \otimes I + I \otimes \pi_2(X) $$ で定義される.
$\Pi_1 \otimes \Pi_2$ および $\pi_1 \otimes \pi_2$ がそれぞれ $G$ および $\mathfrak{g}$ の表現になっていることは容易に確かめられる.この記法は残念ながら曖昧である.なぜなら,$\Pi_1$ と $\Pi_2$ が同じ群 $G$ の表現である場合,$\Pi_1 \otimes \Pi_2$ を $G$ の表現としても $G \times G$ の表現としても考えることができるからである.したがって,$\Pi_1 \otimes \Pi_2$ をどちらの意味で使っているかを明確にしておく必要がある.
$G$の既約表現$\pi_1$と$\pi_2$があるとき,$\pi_1 \otimes \pi_2$は一般に$G$の表現として既約にはならない.したがって,$\pi_1 \otimes \pi_2$を既約表現の直和に分解することを試みる.この分解の理論はClebsch–Gordan理論(物理学では「角運動量の合成」と呼ばれる)と呼ばれる.
$\mathfrak{g}$が有限次元ベクトル空間$V$上に作用するLie代数の表現であるとする.$V^*$は$V$の双対空間(すなわち$V$上の線型汎関数全体の空間)である.$A$が$V$上の線型作用素であるとき,$A^{\mathrm{tr}}$は$V^*$上の双対(または転置)作用素であり, $$ (A^{\mathrm{tr}}\phi)(v) = \phi(Av) $$ で定義される($\phi \in V^*, v \in V$).$v_1, \ldots, v_n$が$V$の基底であれば,それに自然に対応する「双対基底」$\phi_1, \ldots, \phi_n$が存在し,$\phi_j(v_k) = \delta_{jk}$となる.このとき,$A^{\mathrm{tr}}$の双対基底における行列は,元の基底における$A$の行列の単なる転置(共役転置ではない)となる.$A, B$が$V$上の線型作用素であれば, $$ (AB)^{\mathrm{tr}} = B^{\mathrm{tr}} A^{\mathrm{tr}} $$ が容易に確かめられる.
双対表現
$G$が行列Lie群であり,$\Pi$が$G$の表現(有限次元ベクトル空間$V$上に作用)であるとする.このとき,$\Pi$の双対表現$\Pi^*$は,$G$が$V^*$上に作用する表現であり, $$ \Pi^*(g) = [\Pi(g^{-1})]^{\mathrm{tr}} $$ で定義される.また,$\pi$がLie代数$\mathfrak{g}$の表現(有限次元ベクトル空間$V$上に作用)であるとき,$\pi$の双対表現$\pi^*$は,$\mathfrak{g}$が$V^*$上に作用する表現であり, $$ \pi^*(X) = -\pi(X)^{\mathrm{tr}} $$ で定義される.
両方の表現が実際に表現になっていることは容易に確かめられる.双対表現は,反変表現とも呼ばれる.
双対表現の性質
$G$が行列Lie群の表現$\Pi$であれば,(1) $\Pi^*$が既約であることと$\Pi$が既約であることは同値であり,(2) $\Pi^*$と$\Pi$は同型である.Lie代数の表現についても同様の主張が成り立つ.
表現論の多くは,群やLie代数の既約表現を調べることに関係している.状況が良い場合,既約表現を知ることで,すべての表現を記述できるようになる.
完全可約
群やLie代数の有限次元表現が完全可約であるとは,その表現が有限個の既約表現の直和と同型である場合をいう.
完全可約性
群やLie代数が完全可約性を持つとは,その有限次元表現がすべて完全可約である場合をいう.
実際には,ほとんどの群やLie代数は完全可約性を持たない.しかしながら,多くの興味深い例となる群やLie代数はこの性質を持っている.
完全可約性の定理
群やLie代数の表現$V$が完全可約であるとき,次の性質が成り立つ.
- $V$の任意の不変部分空間$U$に対して,別の不変部分空間$W$が存在し,$V$は$U$と$W$の直和として分解できる.
- $V$の任意の不変部分空間も完全可約である.
ユニタリー表現の完全可約性
$G$が行列Lie群であり,$\Pi$が$G$の有限次元ユニタリ表現であれば,$\Pi$は完全可約である.同様に,$\mathfrak{g}$が実Lie代数で,$\pi$が$\mathfrak{g}$の有限次元「ユニタリ」表現(すなわち,すべての$X \in \mathfrak{g}$について$\pi(X)$が歪自己共役作用素)であれば,$\pi$は完全可約である.
コンパクトLie群の完全可約性
$G$がコンパクトな行列Lie群であれば,$G$の任意の有限次元表現は完全可約である.
Schurの補題を群とLie代数の両方について同時に述べられることが望ましい.そのためには,よく使われる記法の濫用を認める必要がある.例えば,$\Pi$が$G$の表現で$V$上に作用している場合,明示的に$\Pi$に言及せずに$V$自体を「表現」と呼ぶことがある.
Schurの補題
- $V$と$W$を群またはLie代数の既約な実または複素表現とし,$\phi: V \to W$を絡写像とする.このとき,$\phi = 0$または$\phi$は同型写像である.
- $V$を群またはLie代数の既約な複素表現とし,$\phi: V \to V$を$V$自身への絡写像とする.このとき,$\phi = \lambda I$(ある$\lambda \in \mathbb{C}$)となる.
- $V$と$W$を群またはLie代数の既約な複素表現とし,$\phi_1, \phi_2: V \to W$を非零な絡写像とする.このとき,$\phi_1 = \lambda \phi_2$(ある$\lambda \in \mathbb{C}$)となる.
定理の最後の2つの主張は,$\mathbb{C}$(または他の代数的閉体)上でのみ成り立ち,$\mathbb{R}$上では成り立たないことに注意.
Schurの補題の系
行列Lie群$G$の既約複素表現$\Pi$があるとする.$A$が$G$の中心に属するなら,ある$\lambda \in \mathbb{C}$について$\Pi(A) = \lambda I$となる.同様に,Lie代数$\mathfrak{g}$の既約複素表現$\pi$があり,$X$が$\mathfrak{g}$の中心に属するなら,ある$\lambda \in \mathbb{C}$について$\pi(X) = \lambda I$となる.
Schurの補題の系2
可換な群またはLie代数の既約複素表現は1次元である.
非常に重要な例として,Lie代数 $\mathfrak{sl}(2,\mathbb{C})$ の有限次元既約複素表現を(同型を除いて)すべて計算する.第一に,$\mathfrak{sl}(2,\mathbb{C})$ は $\mathfrak{su}(2)$ の複素化であり,$\mathfrak{su}(2)$ は $\mathfrak{so}(3)$ と同型であるため,$\mathfrak{so}(3)$ の表現は物理的に重要である.実際,ここでの計算は,量子力学の標準的な教科書で「角運動量」の項目として必ず登場する.第二に,$\mathfrak{su}(2)$ の表現論は,交換関係を用いてLie代数の表現を決定する方法の良い例となる.第三に,半単純Lie代数 $\mathfrak{g}$ の表現を分類する際,$\mathfrak{sl}(2,\mathbb{C})$ の表現論を,$\mathfrak{g}$ の部分代数で $\mathfrak{sl}(2,\mathbb{C})$ と同型なものに対して頻繁に利用することになる.
$\mathfrak{sl}(2,\mathbb{C})$の基底として次のものを用いる: $$ X = \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}, \quad Y = \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix}, \quad H = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} $$ これらは次の交換関係を持つ: $$ [H, X] = 2X, \quad [H, Y] = -2Y, \quad [X, Y] = H $$ $V$が有限次元複素ベクトル空間であり,$A, B, C$が$V$上の作用素で $[A, B] = 2B$, $[A, C] = -2C$, $[B, C] = A$ を満たすとする.括弧演算の歪対称性と双線型性から, $$ \pi(H)=A, \quad \pi(X)=B, \quad \pi(Y)=C $$ と定める一意な線型写像$\pi: \mathfrak{sl}(2,\mathbb{C}) \to \mathfrak{gl}(V)$は,$\mathfrak{sl}(2,\mathbb{C})$の表現となる.
Lie代数 $\mathfrak{sl}(2,\mathbb{C})$ の既約表現
任意の整数 $m \geq 0$ に対して,$\mathfrak{sl}(2,\mathbb{C})$ の既約複素表現で次元が $m+1$ のものが存在する.$\mathfrak{sl}(2,\mathbb{C})$ の既約複素表現で次元が同じもの同士は同型である.
表現空間 $V_m$ は $\pi_m(H)$ の固有ベクトルで張られ,作用素 $\pi_m(X)$ と $\pi_m(Y)$ は固有値を2ずつ上下に移動させる役割を持つ.これと同様の構造が,任意の既約表現で得られる.
先に述べたように,$\mathfrak{sl}(2,\mathbb{C})$ の表現論は,$\mathfrak{sl}(3,\mathbb{C})$ など他の Lie 代数の表現論でも重要な役割を果たす.なぜなら,これらの Lie 代数は $\mathfrak{sl}(2,\mathbb{C})$ と同型な部分代数を含むからである.このような応用のために,既約でない場合も含めた有限次元 $\mathfrak{sl}(2,\mathbb{C})$ の表現について,いくつかの結果が必要となる.
$\mathfrak{sl}(2,\mathbb{C})$ の表現
$\mathfrak{sl}(2,\mathbb{C})$ の有限次元表現 $V$(既約でなくてもよい)について,次の結果が成り立つ.
- $\pi(H)$ のすべての固有値は整数である.さらに,$v$ が $\pi(H)$ の固有ベクトルで固有値 $\lambda$ を持ち,$\pi(X)v = 0$ ならば,$\lambda$ は非負整数である.
- 作用素 $\pi(X)$ および $\pi(Y)$ は冪零である.
- $S: V \to V$ を $$ S = e^{\pi(X)} e^{-\pi(Y)} e^{\pi(X)} $$ で定義すると,$S$ は $$ S \pi(H) S^{-1} = -\pi(H) $$ を満たす.
- 整数 $k$ が $\pi(H)$ の固有値であれば,次の数もすべて固有値となる: $$ -|k|, -|k|+2, -|k|+4, \ldots, |k|-2, |k| $$
$SU(2)$は単連結なので,$\mathfrak{sl}(2,\mathbb{C}) \cong \mathfrak{su}(2)_{\mathbb{C}}$の表現は$SU(2)$の表現と一対一に対応する.また,$SU(2)$はコンパクトなので,$\mathfrak{sl}(2,\mathbb{C})$のすべての表現は完全可約である.
すべてのLie群準同型はLie代数準同型を誘導することが分かっている.特に,行列Lie群のすべての表現は,対応するLie代数の表現を誘導する.結果の部分的な逆を証明できる.すなわち,$G$が単連結な行列Lie群でLie代数を$\mathfrak{g}$とするとき,$\mathfrak{g}$のすべての表現は$G$の表現から得られる.したがって,単連結な行列Lie群$G$については,$G$の表現と$\mathfrak{g}$の表現の間に自然な一対一対応が存在する.
この一般論が $SU(2)$(単連結)と $SO(3)$(単連結でない)の場合にどのように働くかを見ることは有益である.$su(2)$ の任意の既約表現 $\pi$ に対して,その複素化は$sl(2,\mathbb{C})$ の表現 $\pi_m$のいずれかと同型になる.これらの表現は $SU(2)$ の表現から構成されているので,$su(2)$ の任意の既約表現が $SU(2)$ の表現から得られることが直接分かる.
ここで,ある特定の $m$ に対して,群 $SO(3)$ の表現 $\Pi_m$ が存在し,$\Pi_m(\exp X) = \exp(\pi_m(X))$(すべての $X \in \mathfrak{so}(3)$ について)となるかどうかを調べたい.
$SO(3)$の表現
$\mathfrak{so}(3)$の既約複素表現$\sigma_m=\pi_m\circ \phi^{-1}$($m \geq 0$)があるとする.$m$が偶数なら,群$SO(3)$の表現$\Sigma_m$が存在し,すべての$X \in \mathfrak{so}(3)$について$\Sigma_m(\exp X) = \exp(\sigma_m(X))$が成り立つ.$m$が奇数の場合,SO(3)のそのような表現は存在しない.
$m$が偶数であるという条件は,$V_m$の次元$m+1$が奇数であるという条件と同値であることに注意.したがって,群の表現から得られるのは,Lie代数$\mathfrak{so}(3)$の奇数次元表現である.物理学の文献では,$\mathfrak{su}(2) \cong \mathfrak{so}(3)$の表現はパラメータ$l = m/2$でラベル付けされる.この記法では,$\mathfrak{so}(3)$の表現が$SO(3)$の表現から来るのは,$l$が整数の場合に限られる.$l$が整数の表現は「整数スピン」と呼ばれ,それ以外は「半整数スピン」と呼ばれる.
例えば電子は「スピン1/2」粒子であり,これは量子力学において電子が$\mathfrak{so}(3)$の2次元表現によって記述されることを意味する.物理学の文献では,「電子の波動関数に360度回転を作用させると,元の波動関数の符号が反転する」といった記述がよく見られる.この記述は,$SO(3)$の「存在しない」表現$\Sigma_1$を構成しようとすると,$(x, y)$平面内の回転の経路に沿って$\Sigma_1$を定義した場合,$\Sigma_1(I) = -I$となることを反映している.
$\mathfrak{sl}(3,\mathbb{C})$の表現論
ここでは,Lie代数 $\mathfrak{sl}(3,\mathbb{C})$ の表現について調べる.これは群 $SU(3)$ のLie代数の複素化である.主な結果は$\mathfrak{sl}(3,\mathbb{C})$ の既約有限次元表現が「最高ウェイト」によって分類できることである.
ここでの結果は,半単純Lie代数の表現論およびコンパクトLie群の表現論の一般論の特殊な場合である.しかし,$SU(3)$が物理への応用で重要であること,そしてルート・ウェイト・Weyl群といった構造が単純な例で実際にどう働くかを見ることで,これらの構造をより一般的な設定で導入する動機付けとなるため,個別にこの場合を考察することは有用である.
$SU(3)$の有限次元表現(複素ベクトル空間上)は,$\mathfrak{su}(3)$の表現を与え,さらに複素線型性によって $\mathfrak{sl}(3,\mathbb{C}) \cong \mathfrak{su}(3) _\mathbb{C}$ の表現へ拡張できる.$SU(3)$ は単連結なので,逆に $\mathfrak{sl}(3,\mathbb{C})$ の任意の表現を $\mathfrak{su}(3)$ に制限し,指数写像を適用することで $SU(3)$ の表現を得ることができる.$SU(3)$ の表現が既約であることと,対応する $\mathfrak{sl}(3,\mathbb{C})$ の表現が既約であることは同値であり,$SU(3)$ の既約表現と $\mathfrak{sl}(3,\mathbb{C})$ の既約表現の間には一対一対応が成立する.さらに,$SU(3)$ はコンパクト群なので,$SU(3)$ の有限次元表現(したがって $\mathfrak{sl}(3,\mathbb{C})$ の有限次元表現も)はすべて完全可約である.
しかしBaker-Campbell-Hausdorff公式に不必要に頼ることは避けたい.Lie代数の観点から表現を考察すれば,$\mathfrak{sl}(3,\mathbb{C})$ の既約表現は $SU(3)$ の表現から来ることを知らなくても分類できる.もちろん,$\mathfrak{sl}(3,\mathbb{C})$ の既約表現を分類しても,完全可約性を知らなければ一般の表現がどのようなものかは分からない.それでも,$SU(3)$ 群に言及せずに,完全可約性を代数的に証明することは可能である.この証明は一般の半単純Lie代数の設定で与えられることもできるが,$\mathfrak{sl}(3,\mathbb{C})$ の場合に特殊化するのは比較的容易である.
一方,群の観点から表現を考察すると,$\mathrm{SU}(3)$ の既約表現は,$\mathfrak{sl}(3,\mathbb{C})$ の任意の表現が $\mathrm{SU}(3)$ の表現を与えることを知らなくても構成できる.実際,$\mathrm{SU}(3)$ の既約表現は,標準表現とその双対表現の複数個のテンソル積の部分空間として構成される.標準表現とその双対表現は,群 $\mathrm{SU}(3)$ のレベルで直接定義されるため,BCHに頼る必要はない.
要するに,この章では,$SU(3)$および $\mathfrak{sl}(3,\mathbb{C})$ の既約表現の分類を,他の節の結果を使わずに自給自足で示したい.まず $\mathfrak{sl}(3,\mathbb{C})$ について結果を確立し,その後 $SU(3)$ へ移ることにしよう.
$\mathfrak{sl}(3,\mathbb{C})$ の基底として次のものを用いる: \begin{align} H_1=& \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \end{pmatrix}, & H_2=& \begin{pmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{pmatrix}, & & \\ X_1=& \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}, & X_2=& \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{pmatrix}, & X_3=& \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \\ Y_1=& \begin{pmatrix} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}, & Y_2=& \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix}, & Y_3=& \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{pmatrix}. \end{align}
$H_1, X_1, Y_1$の張る部分空間$\langle H_1, X_1, Y_1 \rangle$は,$\mathfrak{sl}(3,\mathbb{C})$の部分代数であり,$\mathfrak{sl}(2,\mathbb{C})$と同型である.これは各行列の第3行・第3列を無視することで分かる.同様に,$\langle H_2, X_2, Y_2 \rangle$も$\mathfrak{sl}(2,\mathbb{C})$と同型な部分代数である.したがって,次の交換関係が成り立つ: \begin{align} [H_1,X_1]=&2X_1,& [H_2,X_2]=&2X_2 \\ [H_1,Y_1]=&-2Y_1,& [H_2,Y_2]=&-2Y_2 \\ [X_1,Y_1]=&H_1,& [X_2,Y_2]=&H_2 \end{align}
次に,$H_1$または$H_2$を含む基底要素同士の交換関係をすべて列挙する(上記の交換関係の一部も含む): \begin{align} [H_1,H_2]=&0, & & \\ [H_1,X_1]=&2X_1, & [H_1,Y_1]=&-2Y_1, \\ [H_2,X_1]=&-X_1 ,& [H_2,Y_1]=&Y_1, \\ [H_1,X_2]=&-X_2, & [H_1,Y_2]=&Y_2, \\ [H_2,X_2]=&2X_2, & [H_2,Y_2]=&-2Y_2, \\ [H_1,X_3]=&X_3, & [H_1,Y_3]=&-Y_3, \\ [H_2,X_3]=&X_3, & [H_2,Y_3]=&-Y_3. \end{align} 最後に,残りの交換関係をすべて列挙する: \begin{align} [X_1,Y_1]=&H_1, & & \\ [X_2,Y_2]=&H_2, & & \\ [X_3,Y_3]=&H_1+H_2, & & \\ [X_1,X_2]=&X_3, & [Y_1,Y_2]=&-Y_3, \\ [X_1,Y_2]=&0, & [X_2,Y_1]=&0, \\ [X_1,X_3]=&0, & [Y_1,Y_3]=&0, \\ [X_2,X_3]=&0, & [Y_2,Y_3]=&0 \\ [X_2,Y_3]=&Y_1, & [X_3,Y_2]=&X_1, \\ [X_1,Y_3]=&-Y_2, & [X_3,Y_1]=&-X_2. \end{align}
以降,$\mathfrak{sl}(3,\mathbb{C})$ の表現の解析はすべて上記の基底に基づいて行う.今後扱う $\mathfrak{sl}(3,\mathbb{C})$ の表現は,すべて有限次元かつ複素線型であると仮定する.
$\mathfrak{sl}(3,\mathbb{C})$ の表現を分類する基本戦略は,$H_1$と$H_2$を同時に対角化することである.$H_1$と$H_2$は可換なので,任意の表現$\pi$に対して$\pi(H_1)$と$\pi(H_2)$も可換となる.したがって,$\pi(H_1)$と$\pi(H_2)$を同時に対角化できる可能性がある.
ウェイト
$\mathfrak{sl}(3,\mathbb{C})$ の表現 $(\pi,V)$ に対して,順序対 $\mu=(m_1, m_2) \in \mathbb{C}^2$ を $\pi$ のウェイトと呼ぶのは,ある $v \neq 0$ が $V$ に存在して $$ \pi(H_1)v = m_1 v, \quad \pi(H_2)v = m_2 v $$ を満たすときである.これを満たす非零ベクトル $v$ を,ウェイト $\mu$ に対応するウェイトベクトルと呼ぶ.ウェイト $\mu$ に対応するすべてのベクトル $v$ からなる空間を,そのウェイトに対応するウェイト空間と呼ぶ.ウェイトの重複度は,対応するウェイト空間の次元である.
したがって,ウェイトとは単に $\pi(H_1)$ と $\pi(H_2)$ の同時固有値の組である.表現が同型であれば,ウェイトとその重複度も一致することは容易に示せる.
ウェイトの存在
任意の $\mathfrak{sl}(3,\mathbb{C})$ の表現は,少なくとも1つのウェイトを持つ.
任意の $\mathfrak{sl}(3,\mathbb{C})$ の表現は,制限することで部分代数 $\langle H_1, X_1, Y_1 \rangle$ および $\langle H_2, X_2, Y_2 \rangle$ の表現とみなすことができる.これらの部分代数はいずれも $\mathfrak{sl}(2,\mathbb{C})$ と同型である.
ウェイトは整数
$\mathfrak{sl}(3,\mathbb{C})$ の表現 $(\pi, V)$ のウェイト $\mu = (m_1, m_2)$ に対して,$m_1$ と $m_2$ はともに整数である.
ここからの戦略は,まず $\pi(H_1)$ と $\pi(H_2)$ の同時固有ベクトルをひとつ取って,$\pi(X_j)$ や $\pi(Y_j)$ を作用させたときにどのような効果があるかを調べることである.以下の定義がこの文脈で重要となる.
ルート
順序対 $\alpha = (a_1, a_2) \in \mathbb{C}^2$ がルートであるとは,
- $a_1$と$a_2$がゼロでないこと,
- 非零な$Z \in \mathfrak{sl}(3,\mathbb{C})$が存在して $$ [H_1,Z]=a_1Z, \quad [H_2,Z]=a_2Z $$ を満たすこと
定義の条件2は,$Z$が$\mathrm{ad}_{H_1}$と$\mathrm{ad}_{H_2}$の同時固有ベクトルであることを意味する.これは,$Z$が随伴表現のウェイトベクトルであり,ウェイトが$(a_1, a_2)$であることを示す.したがって,条件1も考慮すると,ルートとは随伴表現の非零ウェイトに他ならない.交換関係から,$\mathfrak{sl}(3,\mathbb{C})$のルートは次の6つであることが分かる:
| ルート$\alpha$ | $(2, -1)$ | $(-1, 2)$ | $(1, 1)$ | $(-2, 1)$ | $(1, -2)$ | $(-1, -1)$ |
|---|---|---|---|---|---|---|
| ルートベクトル$Z$ | $X_1$ | $X_2$ | $X_3$ | $Y_1$ | $Y_2$ | $Y_3$ |
$H_1$と$H_2$も$\mathrm{ad}_{H_1}$と$\mathrm{ad}_{H_2}$の同時固有ベクトルであるが,同時固有値が両方ともゼロなのでルートベクトルではないことに注意.ルートベクトルと$H_1, H_2$は$\mathfrak{sl}(3,\mathbb{C})$の基底を成すため,上で挙げたもの以外にルートが存在しないことは容易に示せる.これら6つのルートは「ルート系」を形成し,慣例的に$A_2$と呼ばれる(ルート系については後でさらに詳しく扱う).
$X_1$と$X_2$に対応する2つのルートを特に取り出すと便利である: $$ \alpha_1=(2,-1), \quad \alpha_2=(-1,2) $$ これらを正単純ルートと呼ぶ.すべてのルートは,$\alpha_1$と$\alpha_2$の「整数」係数による線型結合として表すことができ,各ルートについてその係数はすべて0以上か,すべて0以下のいずれかである.このことは直接計算で確かめられる: $$ (2,-1)=\alpha_1,\quad (-1,2)=\alpha_2,\quad (1,1)=\alpha_1+\alpha_2 $$ 残りの3つのルートは上記のルートの符号を反転したものである.$\alpha_1$と$\alpha_2$を正単純ルートとする選択は任意であり,同様の性質を持つ他のルートの組でもよい.
$\mathfrak{sl}(3,\mathbb{C})$ の表現論におけるルートの重要性は,次の命題に集約されている.
ルートベクトルは昇降演算子
$\alpha = (a_1, a_2)$ をルートとし,$Z_\alpha \in \mathfrak{sl}(3,\mathbb{C})$ を対応するルートベクトルとする.$\pi$ を $\mathfrak{sl}(3,\mathbb{C})$ の表現,$\mu = (m_1, m_2)$ を $\pi$ のウェイト,$v \neq 0$ を対応するウェイトベクトルとする.このとき, \begin{align} \pi(H_1)\pi(Z_{\alpha})v =& (m_1 + a_1)\pi(Z_{\alpha})v \\ \pi(H_2)\pi(Z_{\alpha})v =& (m_2 + a_2)\pi(Z_{\alpha})v \end{align} すなわち,$\pi(Z_\alpha)v = 0$ であるか,$\pi(Z_\alpha)v$ は新たなウェイトベクトルで,ウェイトは $$ \mu + \alpha = (m_1 + a_1, m_2 + a_2) $$ となる.
ある表現にウェイト $\mu = (m_1, m_2)$ があるとき,ルートベクトル $X_1, X_2, X_3, Y_1, Y_2, Y_3$ を作用させることで,$\mu + \alpha$ という形の新しいウェイトを得ることができる($\alpha$ はルート).もちろん,$\pi(Z_\alpha)v$ がゼロになる場合もあり,その場合 $\mu + \alpha$ は必ずしもウェイトとは限らない.実際,表現が有限次元なので,ウェイトの数も有限であり,しばしばゼロになることが分かる.各表現で「最高ウェイト」を特定し,そこから議論を進めたい.次の定義が「最高ウェイト」の正しい概念を与える.
最高ウェイト
ルート $\alpha_1 = (2, -1)$ および $\alpha_2 = (-1, 2)$ を用いる.2つのウェイト $\mu_1$ と $\mu_2$ があるとき,$\mu_1$ が $\mu_2$ より高い(または同値に,$\mu_2$ が $\mu_1$ より低い)とは,$\mu_1 - \mu_2$ が $$ \mu_1-\mu_2=a\alpha_1+b\alpha_2 $$ の形に書ける場合であり,ここで $a \geq 0$ かつ $b \geq 0$ である.この関係は $\mu_1 \succeq \mu_2$ または $\mu_2 \preceq \mu_1$ と書く.$\mathfrak{sl}(3,\mathbb{C})$ の表現 $\pi$ に対して,$\pi$ のウェイト $\mu_0$ がすべてのウェイト $\mu$ について $\mu \preceq \mu_0$ となるとき,$\mu_0$ を最高ウェイトと呼ぶ.
「高い」という関係は部分順序であることに注意.例えば,$\alpha_1$と$\alpha_2$は,$0$より高くも低くもない.特に,有限個のウェイトの集合が最高ウェイトを持たない場合もある.また,係数$a$や$b$は,$\mu_1$や$\mu_2$が整数成分を持っていても,必ずしも整数である必要はない.例えば,$(1, 0)$は$(0, 0)$より高いが,$(1, 0) = \frac{2}{3}\alpha_1 + \frac{1}{3}\alpha_2$と書ける.
ここで,$\mathfrak{sl}(3,\mathbb{C})$ の既約表現に関する主定理,すなわち「最高ウェイト定理」を述べる準備が整った.
最高ウェイト定理
- $\mathfrak{sl}(3,\mathbb{C})$ の任意の既約表現は,そのウェイト空間の直和として分解される.
- $\mathfrak{sl}(3,\mathbb{C})$ の任意の既約表現は,一意な最高ウェイト $\mu$ を持つ.
- 最高ウェイトが同じである2つの $\mathfrak{sl}(3,\mathbb{C})$ の既約表現は同型である.
- 既約表現の最高ウェイト $\mu$ は $$ \mu=(m_1,m_2) $$ の形であり,$m_1$ と $m_2$ はともに非負整数である.
- 任意の非負整数の組 $(m_1,m_2)$ に対して,最高ウェイト $(m_1,m_2)$ を持つ $\mathfrak{sl}(3,\mathbb{C})$ の既約表現が存在する.
また,群$SU(3)$についても同様の結果を証明する.$SU(3)$の任意の既約表現は,$\mathfrak{sl}(3,\mathbb{C}) \cong \mathfrak{su}(3)_{\mathbb{C}}$ の既約表現を与えるので,$SU(3)$については5を証明することだけが本質的な問題となる.
$SU(3)$の既約表現
任意の非負整数の組 $(m_1, m_2)$ に対して,$SU(3)$ の既約表現 $\Pi$ が存在し,対応する $\mathfrak{sl}(3,\mathbb{C})$ の表現 $\pi$ の最高ウェイトが $(m_1, m_2)$ となる.
$SU(3)$の表現を構成する際,自然に考えられる方法は,$\mathbb{C}^3$ 上の斉次多項式の空間に作用させることである.実際,この方法で $SU(3)$ の表現を構成することができ,得られる表現は既約となる.ただし,$SU(3)$ のすべての既約表現がこの方法で得られるわけではなく,最高ウェイトが $(0, m)$ の形を持つものだけがこの方法で得られる.
$\lambda = (m_1, m_2) \in \mathbb{C}^2$ に対し,$m_1$と$m_2$が整数ならば$\lambda$は整数元であると言い,$m_1$と$m_2$が実数かつ非負ならば$\lambda$はdominantであると言う.したがって,上の定理における可能な最高ウェイトの集合は,dominantな整数元全体である.下図は,$\mathfrak{sl}(3,\mathbb{C})$のルートとdominantな整数元を示している:
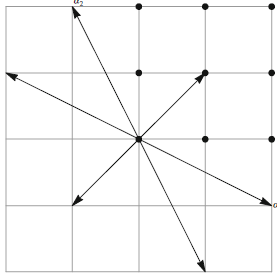
この図は,ウェイト空間の自明な基底を使って描かれている.すなわち,$x$座標は $H_1$ の固有値,$y$座標は $H_2$ の固有値である.後でWeyl群を導入すると,Weyl不変な内積を使ったより対称的な図を描くことができる.
最高ウェイト $(1,1)$ の既約表現を得るには,標準表現とその双対表現のテンソル積を取り,テンソル積の中で最高ウェイトベクトルを選び,さらに作用素 $\pi_{1,1}(Y_j)$($j=1,2,3$)を繰り返し作用させて得られる空間を考える.なお,$Y_3 = -[Y_1, Y_2]$ なので,$\pi_{1,1}(Y_1)$ と $\pi_{1,1}(Y_2)$ だけを作用させれば十分である.
標準表現の最高ウェイトは $e_1$ であり,作用素 $\pi(Y_1) = Y_1$ および $\pi(Y_2) = Y_2$ の作用は次の通り: \begin{align} Y_1 e_1 =& e_2, & Y_1 e_2 =& 0, & Y_1 e_3 =& 0, \\ Y_2 e_1 =& 0, & Y_2 e_2 =& e_3, & Y_2 e_3 =& 0. \end{align} 標準表現の双対については,$Z = Z^{\mathrm{tr}}$ として $\pi(Z) = Z$ とする.新しい基底 $$ f_1 = e_3, \quad f_2 = -e_2, \quad f_3 = e_1 $$ を導入すると,最高ウェイトは $f_1$ となり,次のようになる: \begin{align} \bar{Y_1} f_1 =& 0, & \bar{Y_1} f_2 =& f_3, & \bar{Y_1} f_3 =& 0, \\ \bar{Y_2} f_1 =& -f_2, & \bar{Y_2} f_2 =& 0, & \bar{Y_2} f_3 =& 0. \end{align}
次に,作用素 \begin{align} \pi_{1,1}(Y_1) =& Y_1 \otimes I + I \otimes \bar{Y_1} \\ \pi_{1,1}(Y_2) =& Y_2 \otimes I + I \otimes \bar{Y_2} \end{align} を繰り返し作用させ,ゼロになるまで計算する必要がある.この計算は次の図にまとめられている.ここでは,各ベクトルから2本の矢印が出ている.左の矢印は $Y_1 \otimes I + I \otimes \bar{Y_1}$ の作用,右の矢印は $Y_2 \otimes I + I \otimes \bar{Y_2}$ の作用を示す.スペース節約のため,テンソル積記号は省略し,例えば $e_2 f_2$ のように記す.
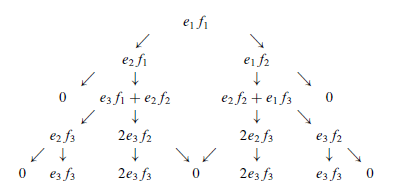
これらのベクトルで張られる空間の基底は,$e_1f_1$, $e_2f_1$, $e_1f_2$, $e_3f_1+e_2f_2$, $e_2f_2+e_1f_3$, $e_2f_3$, $e_3f_2$, $e_3f_3$ である.したがって,この表現の次元は8であり,(同型を除いて)随伴表現となる.$e_1, e_2, e_3$ のウェイトはそれぞれ $(1, 0)$, $(-1, 1)$, $(0, -1)$ であり,$f_1, f_2, f_3$ のウェイトはそれぞれ $(0, 1)$, $(1, -1)$, $(-1, 0)$ である.$e_j \otimes f_k$ のウェイトは $e_j$ のウェイトと $f_k$ のウェイトの和になる.したがって,上記の基底要素のウェイトは $(1, 1)$, $(-1, 2)$, $(2, -1)$, $(0, 0)$(2回), $(1, -2)$, $(-2, 1)$, $(-1, -1)$ となる.各ウェイトの重複度は1だが,$(0, 0)$ のみ重複度2となる.
さて,$SU(3)$の表現に現れる重要な対称性,すなわち「Weyl群」と呼ばれるものについて説明する.ここでの議論は,コンパクト群の枠組みにおける Weyl 群のアプローチに従う.Lie 代数の観点からの Weyl 群については,一般の半単純 Lie 代数の文脈で扱われる.
Cartan 部分代数
$\mathfrak{h}$ を $\mathfrak{sl}(3,\mathbb{C})$ の $H_1$ と $H_2$ で張られる2次元部分空間とする.$N$ を $SU(3)$ の部分群で,すべての $H \in \mathfrak{h}$ に対して $\mathrm{Ad}_A(H)$ が $\mathfrak{h}$ に含まれるような $A \in SU(3)$ 全体の集合とする.$Z$ を $SU(3)$ の部分群で,すべての $H \in \mathfrak{h}$ に対して $\mathrm{Ad}_A(H) = H$ となる $A \in SU(3)$ 全体の集合とする.空間 $\mathfrak{h}$ は $\mathfrak{sl}(3,\mathbb{C})$ の Cartan 部分代数である.
Weyl 群
$SU(3)$ の Weyl 群($W$)は,$N/Z$ という商群で定義される.
coming soon...
半単純 Lie 代数
ここでは,半単純Lie代数というクラスのLie代数を導入する.これらについては,$\mathfrak{sl}(3,\mathbb{C})$で用いた戦略と同様の方法で既約表現を分類できる.ここでは,半単純Lie代数の関連する構造を展開する.
まず「半単純」という用語を定義する.半単純Lie代数には多くの同値な特徴付けが存在するが,これらの特徴付けが同値であることを証明するのは必ずしも容易ではない.ここでは,半単純Lie代数の構造を迅速に展開できる,やや標準的でない定義を用いる.実Lie代数の複素化の概念を思い出そう.
半単純Lie代数
複素Lie代数$\mathfrak{g}$が簡約であるとは,あるコンパクト行列Lie群$K$が存在して $$ \mathfrak{g} \cong \mathfrak{k}_{\mathbb{C}} $$ となる場合をいう.複素Lie代数$\mathfrak{g}$が半単純であるとは,$\mathfrak{g}$が簡約であり,かつ$\mathfrak{g}$の中心が自明(ゼロ)の場合をいう.
コンパクト実形式
$\mathfrak{g}$が半単純Lie代数であるとき,$\mathfrak{g}$の実部分代数$\mathfrak{k}$が$\mathfrak{g}$のコンパクト実形式であるとは,$\mathfrak{k}$があるコンパクト行列Lie群のLie代数と同型であり,$\mathfrak{g}$の任意の元$Z$が一意的に$Z = X + iY$($X, Y \in \mathfrak{k}$)の形に書ける場合をいう.
この定義を用いることでCartan部分代数の構成が容易になり,後で扱うコンパクトLie群の研究とも自然に結びつく.他方で,この定義は,より標準的な定義に比べて一見するとより狭いクラスのLie代数しか扱えないように見える.すなわち,定義の条件は「半単純」の標準的な定義のうち2つを含意することを証明するが,逆の含意は証明しない.実際には逆の含意も成り立つので,最終的には我々の半単純性の定義は他のどの定義とも同値である.しかし,この定義による効率性を損なわずに逆の含意を証明することはできない.より伝統的な半単純性の定義から理論を展開したい読者は,[Kna2]の第II章(および第I章の最初のいくつかの節)を参照されたい.
この定義でコンパクト群を用いるのは,内積を構成する場合のみである.標準的な半単純Lie代数の扱いでは,内積の代わりにKilling形式が用いられる.我々が双線型なKilling形式の代わりに内積を使うことで,いくつかの議論が大幅に簡単になる.特に,Cartan部分代数の構成では,歪自己共役作用素が常に対角化可能であることを利用する.一方,非退化な双線型形式に関して歪対称な作用素は必ずしも対角化可能とは限らない.そのため,従来のアプローチによるCartan部分代数の構成は,我々の方法よりもかなり複雑になる.
複素半単純Lie代数$\mathfrak{g}$については,常に$\mathfrak{g}$のコンパクト実形式$\mathfrak{k}$を選んでいると仮定する.すなわち,$\mathfrak{g} \cong \mathfrak{k}_{\mathbb{C}}$である.
(少しskip)
Lie代数$\mathfrak{g}$が単純であるとは,$\mathfrak{g}$が非自明なイデアルを持たず,かつ$\dim \mathfrak{g} \geq 2$である場合をいった.すなわち,1次元のLie代数は,非自明なイデアルを持たないが,定義により単純とはみなされない.
半単純Lie代数の分解
$\mathfrak{g}$が半単純であるとする.このとき,$\mathfrak{g}$はLie代数の直和として $$ \mathfrak{g} = \bigoplus_{j=1}^m \mathfrak{g}_j $$ の形に分解される.ここで,各$\mathfrak{g}_j \subset \mathfrak{g}$は単純Lie代数である.
半単純Lie代数の例のほとんどは実際には単純であり,分解の項が1つだけになる. また,逆も成り立つ.すなわち,複素Lie代数$\mathfrak{g}$が単純Lie代数の直和として分解されるなら,$\mathfrak{g}$は半単純である.
分解の一意性
$\mathfrak{g}$が複素半単純Lie代数である場合,分解に現れる部分代数$\mathfrak{g}_j$は順序を除いて一意である.
より厳密に言えば,$\mathfrak{g}$が単純部分代数$\mathfrak{g}_1, \ldots, \mathfrak{g}_l$のLie代数の直和に同型であり,また単純部分代数$\mathfrak{h}_1, \ldots, \mathfrak{h}_m$のLie代数の直和にも同型であると仮定する.このとき,この命題は各$\mathfrak{h}_j$が,ある$k$について実際に(同型ではなく)$\mathfrak{g}_k$と等しいことを主張している.この命題は,分解の各成分$\mathfrak{g}_j$が単純(したがって$\dim \mathfrak{g}_j \geq 2$)であることに本質的に依存しており,単に$\mathfrak{g}_j$が非自明なイデアルを持たないだけでは十分ではない.実際,$\mathfrak{g}$が2次元の可換Lie代数であれば,$\mathfrak{g}$は1次元の可換Lie代数の直和として多くの異なる方法で分解できる.
半単純Lie代数の詳細に入る前に,その表現を分類する際の戦略と必要となる構造について簡単に概観しよう.まず,Lie代数内で可換な元$H_1, \ldots, H_r$を探し,それらを各表現で同時に対角化しようとする.このような元はできるだけ多く見つけるべきであり,すべての表現で同時対角化できるためには,随伴表現でも対角化可能でなければならない.このことは(基底に依存しない言葉で)Cartan部分代数の定義につながる.随伴作用$\mathrm{ad}_{H_1}, \ldots, \mathrm{ad}_{H_r}$の同時固有値の非零な組を「ルート」と呼び,対応する同時固有ベクトルを「ルートベクトル」と呼ぶ.ルートベクトルは,各表現$\pi$において$\pi(H_1), \ldots, \pi(H_r)$の固有値を昇降させる役割を果たす.また,Weyl群という重要な対称性があり,これはルート系や各表現のウェイト系の対称性となる.
半単純Lie代数の構造において本質的なのは,$\mathfrak{sl}(2,\mathbb{C})$と同型な特別な部分代数が存在することである.この節および以降の節で,これらの部分代数に対して$\mathfrak{sl}(2,\mathbb{C})$の表現論の知識を何度も利用することになる.$X, Y, H$が$\mathfrak{sl}(2,\mathbb{C})$の標準的な基底要素であるとき,特に重要なのは,$\mathfrak{sl}(2,\mathbb{C})$の任意の有限次元表現$\pi$(既約でなくてもよい)において,$\pi(H)$のすべての固有値が整数でなければならないという事実である.
最初の課題は,「Cartan部分代数」と呼ばれる特別な種類の可換部分代数を特定することである.
Cartan部分代数
$\mathfrak{g}$が複素半単純Lie代数であるとき,$\mathfrak{g}$のCartan部分代数($\mathfrak{h}$)とは,$\mathfrak{g}$の複素部分空間$\mathfrak{h}$で,以下の性質を満たすものである:
- 任意の$H_1, H_2 \in \mathfrak{h}$について,$[H_1, H_2] = 0$が成り立つ.
- ある$X \in \mathfrak{g}$が,すべての$H \in \mathfrak{h}$について$[H, X] = 0$を満たすなら,$X \in \mathfrak{h}$である.
- 任意の$H \in \mathfrak{h}$について,随伴作用$\mathrm{ad}_H$は対角化可能である.
条件1は,$\mathfrak{h}$が$\mathfrak{g}$の可換部分代数であることを意味する.条件2は,$\mathfrak{h}$が極大可換部分代数(すなわち,より大きな可換部分代数に含まれない)であることを意味する.条件3は,各$H \in \mathfrak{h}$について随伴作用$\mathrm{ad}_H$が対角化可能であることを意味する.$\mathfrak{h}$内の$H$同士は可換なので,$\mathrm{ad}_H$同士も可換となり,したがって同時に対角化可能である.
もちろん,Cartan部分代数の定義は任意のLie代数に対して意味を持つが,$\mathfrak{g}$が半単純でない場合,Cartan部分代数を持たないこともある(すべての複素Lie代数がCartan部分代数を持つような,別の「Cartan部分代数」の定義も使われることがある.この別定義は,$\mathfrak{g}$が半単純な場合には上の定義と同値だが,一般には同値ではない).半単純の場合でさえ,Cartan部分代数が存在することを証明する必要がある.
Cartan部分代数の存在
$\mathfrak{g} = \mathfrak{k}_{\mathbb{C}}$ を複素半単純Lie代数とし,$\mathfrak{t}$ を $\mathfrak{k}$ の任意の極大可換部分代数とする.$\mathfrak{h} \subset \mathfrak{g}$ を $$ \mathfrak{h} = \mathfrak{t}_{\mathbb{C}} = \mathfrak{t} + i\mathfrak{t} $$ と定める.このとき,$\mathfrak{h}$ は $\mathfrak{g}$ のCartan部分代数である.
$\mathfrak{k}$(または任意の有限次元Lie代数)は,必ず極大可換部分代数を含むことに注意.実際,任意の1次元部分代数$\mathfrak{t}_1$は可換である.もし$\mathfrak{t}_1$が極大ならそれでよいし,そうでなければ$\mathfrak{t}_1$を真に含む可換部分代数$\mathfrak{t}_2$を選び,この操作を繰り返すことで極大可換部分代数が得られる.
この節および以降の節では,すべてのCartan部分代数を,あるコンパクト実形式$\mathfrak{k}$の極大可換部分代数$\mathfrak{t}$を用いて$\mathfrak{h} = \mathfrak{t}_{\mathbb{C}}$の形で考えることにする.実際,すべてのCartan部分代数はこのような形で得られるが,これは自明ではない.さらに,$\mathfrak{g}$の任意の2つのCartan部分代数$\mathfrak{h}_1, \mathfrak{h}_2$に対して,$\mathfrak{h}_1$を$\mathfrak{h}_2$に写す$\mathfrak{g}$の自己同型が存在する.この結果の証明は省略するが,後で,固定した$\mathfrak{k}$に対して極大可換部分代数$\mathfrak{t} \subset \mathfrak{k}$は自己同型によって一意であることを示す.Cartan部分代数が自己同型によって一意であることから,次の定義が意味を持つことになる.
階数
$\mathfrak{g}$が複素半単純Lie代数であるとき,$\mathfrak{g}$の階数とは,任意のCartan部分代数の次元である.
この節の残りでは,複素半単純Lie代数$\mathfrak{g}$に対して,コンパクト実形式$\mathfrak{k}$とその極大可換部分代数$\mathfrak{t}$を選び,Cartan部分代数$\mathfrak{h} = \mathfrak{t} + i\mathfrak{t}$として考えることにする.また,$\mathfrak{g}$上に,$\mathfrak{k}$上で実数値をとり,$K$の随伴作用に関して不変な内積を選んでいると仮定する.
随伴作用素 $\mathrm{ad}_H$($H \in \mathfrak{h}$)同士は可換であり,各 $\mathrm{ad}_H$ は対角化可能なので,すべての $\mathrm{ad}_H$($H \in \mathfrak{h}$)は同時に対角化可能である.$X \in \mathfrak{g}$ がすべての $\mathrm{ad}_H$($H \in \mathfrak{h}$)の同時固有ベクトルであるとき,対応する固有値は $H \in \mathfrak{h}$ に対して線型に依存する.この線型汎関数が非零であれば,これを「ルート」と呼ぶ.この線型汎関数は $H \mapsto \langle \alpha, H \rangle$ の形($\alpha \in \mathfrak{h}$)で表すと便利である.以上の議論から,次の定義が導かれる.
ルート
$\mathfrak{g}$が複素半単純Lie代数で,$\mathfrak{h}$がそのCartan部分代数であるとする.$\mathfrak{h}$の非零元$\alpha$がルート($\mathfrak{h}$に関する$\mathfrak{g}$のルート)であるとは,非零な$X \in \mathfrak{g}$が存在して,すべての$H \in \mathfrak{h}$について $$ [H, X] = \langle \alpha, H \rangle X $$ が成り立つ場合をいう.すべてのルートの集合を$R$と表す.
ここで,内積は第2成分について線型であるという慣習に従うことに注意する.したがって,$\langle \alpha, H \rangle$ は,$\alpha$ を固定したとき $H$ に関して線型に依存する.
ルートの所属
各ルート $\alpha$ は $i\mathfrak{t} \subset \mathfrak{h}$ に属する.
ルート空間
$\alpha$がルートであるとき,ルート空間$\mathfrak{g}_\alpha$は,すべての$H \in \mathfrak{h}$について$[H, X] = \langle \alpha, H \rangle X$を満たす$\mathfrak{g}$の元$X$全体の空間である.$\mathfrak{g}_\alpha$の非零元を,ルート$\alpha$に対応するルートベクトルと呼ぶ.
より一般に,$\alpha$が$\mathfrak{h}$の任意の元であるとき,$\mathfrak{g}_\alpha$を,すべての$H \in \mathfrak{h}$について$[H, X] = \langle \alpha, H \rangle X$を満たす$\mathfrak{g}$の元$X$全体の空間と定義する(ただし,$\alpha$が実際にルートである場合のみ$\mathfrak{g}_\alpha$をルート空間と呼ぶ).
$\alpha = 0$ の場合,$\mathfrak{g}_0$ は $\mathfrak{h}$ のすべての元と可換な $\mathfrak{g}$ の元全体の集合となる.$\mathfrak{h}$ が極大可換部分代数であるため,$\mathfrak{g}_0 = \mathfrak{h}$ となる.$\alpha$ がゼロでなく,かつルートでない場合,$\mathfrak{g}_\alpha = \{0\}$ となる.
すでに述べたように,随伴作用素 $\mathrm{ad}_H$($H \in \mathfrak{h}$)は同時に対角化可能である.その結果,$\mathfrak{g}$ は $\mathfrak{h}$ とルート空間 $\mathfrak{g}_\alpha$ の和として分解できる.
Lie代数の分解
Lie代数 $\mathfrak{g}$ は,ベクトル空間の直和として次のように分解できる: $$ \mathfrak{g} = \mathfrak{h} \oplus \bigoplus_{\alpha \in R} \mathfrak{g}_\alpha $$
すなわち,$\mathfrak{g}$ の任意の元は,一意的に $\mathfrak{h}$ の元と各ルート空間 $\mathfrak{g}_\alpha$ の元の和として書くことができる.ただし,この分解は Lie 代数の直和ではないことに注意.例えば,$\mathfrak{h}$ の元と $\mathfrak{g}_\alpha$ の元は一般には可換ではない.
ルートの和
任意の $\alpha, \beta \in \mathfrak{h}$ に対して, $$ [\mathfrak{g}_{\alpha},\mathfrak{g}_{\beta}] \subset \mathfrak{g}_{\alpha + \beta} $$
特に,$X$が$\mathfrak{g}_\alpha$に属し,$Y$が$\mathfrak{g}_{-\alpha}$に属する場合,$[X, Y]$は$\mathfrak{h}$に属する.また,$X$が$\mathfrak{g}_\alpha$,$Y$が$\mathfrak{g}_\beta$に属し,$\alpha+\beta$がゼロでもルートでもない場合,$[X, Y]=0$が成り立つ.
ルートの性質1
- $\alpha \in \mathfrak{h}$ がルートであれば,$-\alpha$ もルートである.具体的には,$X \in \mathfrak{g}_\alpha$ ならば $X^*$ は $\mathfrak{g}_{-\alpha}$ に属する.
- すべてのルートは $\mathfrak{h}$ を張る.
ここで,半単純Lie代数$\mathfrak{g}$の研究における重要な道具を展開する.$\mathfrak{g}$の中に$\mathfrak{sl}(2,\mathbb{C})$と同型な部分代数が存在することが本質的である.
半単純Lie代数内の$\mathfrak{sl}(2,\mathbb{C})$部分代数
各ルート $\alpha$ に対して,$\mathfrak{g}_\alpha$ 内に線型独立な元 $X_\alpha$,$\mathfrak{g}_{-\alpha}$ 内に $Y_\alpha$,$\mathfrak{h}$ 内に $H_\alpha$ を取ることができる.ここで,$H_\alpha$ は $\alpha$ の定数倍であり,次の関係式を満たす: \begin{align} [H_{\alpha}, X_\alpha] &= 2 X_\alpha \\ [H_{\alpha}, Y_\alpha] &= -2 Y_\alpha \\ [X_\alpha, Y_\alpha] &= H_\alpha \end{align} さらに,$Y_\alpha$ は $X_{\alpha}^*$ と等しく取ることができる.
$X_\alpha, Y_\alpha, H_\alpha$ が上の定理のように与えられているとする.一方で $[H_\alpha, X_\alpha] = 2X_\alpha$ であり,また $[H_\alpha, X_\alpha] = \langle \alpha, H_\alpha \rangle X_\alpha$ でもある.したがって, $$ \langle \alpha, H_\alpha \rangle = 2 $$ また,$H_\alpha$ は $\alpha$ の定数倍であり,条件を満たす唯一の定数倍は $$ H_{\alpha} = 2\frac{\alpha}{\langle \alpha, \alpha \rangle} $$
半単純Lie代数内の$\mathfrak{sl}(2,\mathbb{C})$部分代数
各ルート $\alpha$ に対して,$X_\alpha, Y_\alpha, H_\alpha$ を上の定理のように取る($Y_\alpha = X_\alpha^*$ とする).このとき, $$ E_1^{\alpha} \equiv \frac{i}{2} H_{\alpha}, \quad E_2^{\alpha} \equiv \frac{i}{2}(X_{\alpha}+Y_{\alpha}), \quad E_3^{\alpha} \equiv \frac{1}{2}(Y_{\alpha}-X_{\alpha}) $$ は$\mathfrak{k}$の線型独立な元であり,次の交換関係を満たす: $$ [E_1^{\alpha},E_2^{\alpha}]=E_3^{\alpha}, \quad [E_2^{\alpha},E_3^{\alpha}]=E_1^{\alpha}, \quad [E_3^{\alpha},E_1^{\alpha}]=E_2^{\alpha} $$ よって,$E_1^{\alpha}, E_2^{\alpha}, E_3^{\alpha}$の張る部分空間は$\mathfrak{su}(2)$と同型な$\mathfrak{k}$の部分代数となる.
コルート
上の定理における $H_\alpha = 2\alpha / \langle \alpha, \alpha \rangle$ を,ルート $\alpha$ に対応するコルートと呼ぶ.
上の定理で得られた部分代数を用いて,ルートおよびルート空間に関する結果を導く.注意すべきは, $$ \mathfrak{s}^{\alpha} \equiv \langle X_{\alpha}, Y_{\alpha}, H_{\alpha} \rangle $$ が,随伴表現($\mathfrak{s}^{\alpha}$への制限)によって$\mathfrak{g}$上に作用することである.
ルートの性質2
- 各ルート $\alpha$ について,$\alpha$ の倍数でルートとなるのは $\alpha$ と $-\alpha$ のみである.
- 各ルート $\alpha$ について,ルート空間 $\mathfrak{g}_\alpha$ は1次元である.
ここで,ルート集合 $R$ の重要な対称性である「Weyl群」を導入する.この節では,Lie群的アプローチではなく,Lie代数的アプローチに従ってWeyl群を定義する.
Weyl群
各ルート $\alpha \in R$ に対して,線型写像 $s_\alpha: \mathfrak{h} \to \mathfrak{h}$ を $$ s_{\alpha}\cdot H = H -2 \frac{\langle \alpha, H \rangle}{\langle \alpha, \alpha \rangle} \alpha $$ で定義する.ルート系 $R$ の Weyl 群$W$は,すべての $s_\alpha$($\alpha \in R$)で生成される $\mathrm{GL}(\mathfrak{h})$ の部分群である.
各ルート $\alpha$ が $i\mathfrak{t}$ に属し,内積が $\mathfrak{t}$ 上で実数値をとることから,$H$ が $i\mathfrak{t}$ に属する場合,$s_\alpha \cdot H$ も $i\mathfrak{t}$ に属することに注意.$i\mathfrak{t}$ への写像として,$s_\alpha$ は $\alpha$ に直交する超平面についての反射である.すなわち,$H$ が $\alpha$ に直交していれば $s_\alpha \cdot H = H$ となり,$s_\alpha \cdot \alpha = -\alpha$ となる.各反射は直交線型変換なので,$W$ は直交群 $O(i\mathfrak{t})$ の部分群となる.
Weyl群の性質
$W$ の $i\mathfrak{t}$ 上での作用はルート集合 $R$ を保つ.すなわち,$\alpha$ がルートであれば,任意の $w \in W$ について $w \cdot \alpha$ もルートである.
実際,$s_\alpha \cdot s_\alpha \cdot \beta = \beta$ であるため,各反射は $R$ を $R$ へ写す.したがって,任意の $w \in W$ についても $R$ を $R$ へ写すことが分かる.
Weyl群は有限
Weyl群は有限群である.
さて,ルートに関するいくつかの重要な性質をまとめる.各ルート$\alpha$に対して,$\mathfrak{h}$内に$H_\alpha$という元が存在する.$H_\alpha$は$\langle \alpha, H_\alpha \rangle = 2$を満たし,$\alpha$との関係式$H_\alpha = 2\alpha / \langle \alpha, \alpha \rangle$で与えられる.特に,$H_\alpha$は$X_\alpha$や$Y_\alpha$の選び方に依存しない.
コルート
各ルート $\alpha$ に対して,$\mathfrak{h}$ 内の元 $H_\alpha$ を $$ H_\alpha = 2\frac{\alpha}{\langle \alpha, \alpha \rangle} $$ で定める.これはルート $\alpha$ に対応するコルートである.
ルートの性質3
すべてのルート $\alpha, \beta$ に対して, $$ \langle \beta, H_{\alpha} \rangle = 2 \frac{\langle \alpha, \beta \rangle}{\langle \alpha, \alpha \rangle} $$ は整数となる.
初等線型代数から,$\alpha$と$\beta$が内積空間の元であるとき,$\beta$の$\alpha$への直交射影は $$ \frac{\langle \alpha, \beta \rangle}{\langle \alpha, \alpha \rangle} \alpha $$ で与えられることを思い出そう.上の定理の右辺の量は,$\beta$の$\alpha$への射影における$\alpha$の係数の2倍である.したがって,定理の整数性の結果は次のような幾何学的解釈ができる:$\alpha$と$\beta$がルートであれば,$\alpha$の$\beta$への直交射影は$\beta$の整数倍または半整数倍でなければならない.あるいは,定理は,$\beta$と$s_\alpha \cdot \beta$が$\alpha$の整数倍だけ異なることを述べていると考えることもできる.
ルート集合 $R$ を実内積空間 $i\mathfrak{t}$ の部分集合とみなすと,$R$ の性質は次のようにまとめられる.
ルートの性質 まとめ
ルート集合 $R$ は,実内積空間 $E$ の零でない元からなる有限集合であり,次の性質を持つ:
- ルートは $E$ を張る.
- $\alpha \in R$ ならば $-\alpha \in R$ であり,$R$ に含まれる $\alpha$ の倍数は $\alpha$ と $-\alpha$ のみである.
- $\alpha, \beta \in R$ ならば,$s_\alpha \cdot \beta$ も $R$ に含まれる.ただし $s_\alpha$ は反射である.
- すべての $\alpha, \beta \in R$ について, $$ 2\frac{\langle \alpha, \beta \rangle}{\langle \alpha, \alpha \rangle} $$ は整数となる.
このようなベクトルの集合は「ルート系」と呼ばれる.ルート系の性質については後で詳しく扱う.
すべての半単純Lie代数は単純Lie代数の直和として分解される.ここでは,半単純Lie代数が単純であるための判定基準を与える.よく知られた半単純Lie代数のほとんどは実際には単純である.
単純Lie代数の判定
$\mathfrak{g}$が実Lie代数であり,その複素化$\mathfrak{g}_\mathbb{C}$が単純であるとする.このとき,$\mathfrak{g}$も単純である.
逆は一般には成り立たない.例えば,Lie代数 $\mathfrak{so}(3)$ は実Lie代数として単純だが,その複素化は $\mathfrak{so}(4,\mathbb{C})$ と同型であり,さらに $\mathfrak{so}(4,\mathbb{C})$ は $\mathfrak{sl}(2,\mathbb{C}) \oplus \mathfrak{sl}(2,\mathbb{C})$ と同型である.
単純Lie代数の判定2
$K$ をコンパクトな行列 Lie 群とし,その Lie 代数 $\mathfrak{k}$ が実 Lie 代数として単純であるとする.このとき,$\mathfrak{k}$ の複素化 $\mathfrak{g} = \mathfrak{k}_\mathbb{C}$ は複素 Lie 代数として単純である.
複素構造を持つ
実Lie代数$\mathfrak{g}$が複素構造を持つとは,$\mathfrak{g}$上に「$i$倍」写像$J: \mathfrak{g} \to \mathfrak{g}$が存在し,これによって$\mathfrak{g}$が複素ベクトル空間となり,かつbracket演算$[\bullet, \bullet]: \mathfrak{g} \times \mathfrak{g} \to \mathfrak{g}$が複素双線型となる場合をいう.
ここで,bracket 演算の双線型性とは,特に $[iX, Y] = i[X, Y]$ がすべての $X, Y \in \mathfrak{g}$ について成り立つことを意味する.同値な定義として,実 Lie 代数 $\mathfrak{g}$ が複素構造を持つとは,ある複素 Lie 代数 $\mathfrak{h}$ と実線型な全単射 $\varphi: \mathfrak{h} \to \mathfrak{g}$ が存在し,すべての $X, Y \in \mathfrak{h}$ について $\varphi([X, Y]) = [\varphi(X), \varphi(Y)]$ が成り立つ場合をいう.
複素構造を持たないLie代数
$K$ をコンパクトな行列 Lie 群とし,その Lie 代数 $\mathfrak{k}$ が非可換であるとする.このとき,$\mathfrak{k}$ は複素構造を持たない.
単純Lie代数の判定3
$\mathfrak{g} = \mathfrak{k}_{\mathbb{C}}$ を複素半単純Lie代数とし,$\mathfrak{t}$ を $\mathfrak{k}$ の極大可換部分代数,$\mathfrak{h} = \mathfrak{t}_{\mathbb{C}}$ を対応するCartan部分代数とする.$R \subset \mathfrak{h}$ を $\mathfrak{g}$ のルート系とする.$\mathfrak{g}$ が単純でない場合,$\mathfrak{h}$ は直交する非零部分空間 $\mathfrak{h}_1$ と $\mathfrak{h}_2$ の直和として分解され,$R$ のすべての元は $\mathfrak{h}_1$ または $\mathfrak{h}_2$ のいずれかに属する.逆に,$\mathfrak{h}$ がこのように分解できるなら,$\mathfrak{g}$ は単純ではない.
この定理の最初の部分は,反対の形で言い換えることもできる:もし $\mathfrak{h}$ を $\mathfrak{h}_1$ と $\mathfrak{h}_2$ の直交直和 $\mathfrak{h} = \mathfrak{h}_1 \oplus \mathfrak{h}_2$(ただし $\dim \mathfrak{h}_1 > 0, \dim \mathfrak{h}_2 > 0$)として分解できて,すべてのルートが $\mathfrak{h}_1$ または $\mathfrak{h}_2$ のいずれかに属する,という分解が存在しないなら,$\mathfrak{g}$ は単純である.後でルート系の「Dynkin図」が連結であれば,そのような $\mathfrak{h}$ の分解は存在しないことを示す.これによって,半単純Lie代数のほとんどの例が実際には単純であることを確認できる.
さて,これまでに述べた構造が「古典的」半単純Lie代数の場合(すなわち,複素数体上の特殊線型代数,直交代数,シンプレクティック代数)でどのように現れるかを見ていく.各Lie代数は階数が$n$となるようにラベル付けし,直交代数については偶数次と奇数次の場合に分けて解析する.古典的Lie代数のそれぞれについて,対応するコンパクト群の随伴作用に関して不変なHilbert-Schmidt内積($\langle X, Y\rangle = \mathrm{trace}(X^* Y)$の定数倍)を用いる.
コンパクト実形式 $\mathfrak{k} \equiv \mathfrak{su}(n+1)$ と,$\mathfrak{su}(n+1)$ 内の対角行列全体の集合との交わりである可換部分代数 $\mathfrak{t}$ を考える.すなわち, $$ \mathfrak{t} = \left\{ \mathrm{diag}(ia_1, ia_2, \ldots, ia_{n+1}) \mid a_j \in \mathbb{R},\ a_1+\cdots+a_{n+1} = 0 \right\} $$ また,$\mathfrak{h} \equiv \mathfrak{t}_{\mathbb{C}}$ も考える.これは次のように記述できる: $$ \mathfrak{h} = \left\{ \mathrm{diag}(\lambda_1, \lambda_2, \ldots, \lambda_{n+1}) \mid \lambda_j \in \mathbb{C},\ \lambda_1+\cdots+\lambda_{n+1} = 0 \right\} $$
行列 $X$ が $\mathfrak{t}$ のすべての元と可換であれば,$\mathfrak{h}$ のすべての元とも可換になる.しかし,$X$ は対角行列でなければならず,もし $X \in \mathfrak{su}(n+1)$ ならば $X$ は $\mathfrak{t}$ に属することになる.したがって,$\mathfrak{t}$ は実際に $\mathfrak{su}(n+1)$ の極大可換部分代数である.
ここで,$E_{jk}$ を $j$ 行 $k$ 列に 1 があり,それ以外は 0 の行列とする.簡単な計算により,$H \in \mathfrak{h}$ が上のような対角行列であれば, $$ H E_{jk} = \lambda_j E_{jk}, \quad E_{jk} H = \lambda_k E_{jk} $$ となる.したがって, $$ [H, E_{jk}] = (\lambda_j - \lambda_k) E_{jk} $$ $j \neq k$ のとき,$E_{jk}$ は $\mathfrak{sl}(n+1, \mathbb{C})$ に属し,$E_{jk}$ は各 $H \in \mathfrak{h}$ に対する随伴作用 $\mathrm{ad}_H$ の同時固有ベクトルであり,固有値は $\lambda_j - \lambda_k$ となる.任意の $X \in \mathfrak{sl}(n+1, \mathbb{C})$ は,Cartan 部分代数($X$ の対角成分)と,$j \neq k$ の $E_{jk}$ の線型結合($X$ の非対角成分)の和として一意的に書ける.
まずルートを$\mathfrak{h}^*$の元と考えると,ルートは各$H \in \mathfrak{h}$に対して$\lambda_j - \lambda_k$という値を割り当てる線型汎関数$\alpha_{jk}$となる.$\mathfrak{h}$は,成分の和がゼロとなる$\mathbb{C}^{n+1}$の部分空間と同一視できる.$\mathfrak{h}$上の内積$\langle X, Y \rangle = \mathrm{trace}(X^* Y)$は,通常の$\mathbb{C}^{n+1}$上の内積をこの部分空間に制限したものである.この内積を使ってルートを$\mathfrak{h}^*$から$\mathfrak{h}$へ移すと,次のベクトルが得られる: $$ \alpha_{jk} = e_j - e_k \quad (j \neq k) $$
$\mathfrak{sl}(n+1, \mathbb{C})$ のルートは,慣例的に $A_n$ と呼ばれるルート系を形成する.ここで,$n$ は $\mathfrak{sl}(n+1, \mathbb{C})$ の階数(すなわち Cartan 部分代数 $\mathfrak{h}$ の次元)を表す.各ルートの長さは $\sqrt{2}$ であり, $$ \langle \alpha_{jk}, \alpha_{j'k'} \rangle $$ の値は,$\{j, k\}$ と $\{j', k'\}$ の共通要素の数によって 0, $\pm1$, $\pm2$ となる.したがって, $$ 2\frac{\langle \alpha_{jk}, \alpha_{j'k'} \rangle}{\langle \alpha_{jk}, \alpha_{jk} \rangle} \in \{0, \pm1, \pm2\} $$ $\alpha$ と $\beta$ がルートで,$\alpha \neq \beta$ かつ $\alpha \neq -\beta$ のとき,$\alpha$ と $\beta$ のなす角は,$\langle \alpha, \beta \rangle$ の値が 1, 0, $-1$ の場合にそれぞれ $\pi/3$, $\pi/2$, $2\pi/3$ となる.
任意の $j, k$ について,反射 $s_{jk}$ は $\mathbb{C}^{n+1}$ 上で各ベクトルの $j$ 番目と $k$ 番目の成分を入れ替える作用を持つことは容易に分かる.したがって,$A_n$ ルート系の Weyl 群は $n+1$ 個の要素からなる置換群(対称群)となる.
ルート系
この節では,半単純Lie代数から独立にルート系を考察する.ここで確立する様々な「事実」は,以降の節で頻繁に利用される.ルート系に関する結果がどのように使われるかの一例を挙げよう.次節では,半単純Lie代数の有限次元既約表現を,Verma加群と呼ばれる無限次元表現の商として構成する.この商表現が有限次元であることを示すために,商表現のウェイトがWeyl群の作用で不変であることを示す.Weyl群とは,ルートに直交する超平面に関する反射で生成される群である.しかし,すべての反射に対してウェイトが不変であることを直接証明することはできず,ルート系の特別な部分集合である「基底」に対応する反射についてのみ証明できる.したがって,議論を完成させるには,Weyl群が実際に基底のルートに対応する反射によって生成されることを知る必要がある.
ルート系とは,半単純Lie代数のルート($i\mathfrak{t}$の部分集合として見たもの)が満たす性質を持つベクトルの集合のことであり,次の定義にまとめられる.
ルート系
ルート系$(E,R)$とは,有限次元実ベクトル空間 $E$(内積 $\langle \bullet, \bullet \rangle$ を持つ)と,その中の有限個の零でないベクトルの集合 $R$ で,以下の性質を満たすものである:
- $R$ のベクトルは $E$ を張る.
- $\alpha \in R$ と実数 $c$ について,$c\alpha \in R$ となるのは $c = \pm 1$ の場合のみである.
- $\alpha, \beta \in R$ ならば,$s_\alpha \cdot \beta$ も $R$ に含まれる.ただし $s_\alpha$ は $E$ 上の線型変換で $$ s_{\alpha}\cdot \beta = \beta -2\frac{\langle \beta, \alpha \rangle}{\langle \alpha, \alpha \rangle} \alpha \quad (\beta \in E) $$ で定義される.
- すべての $\alpha, \beta \in R$ について, $$ 2\frac{\langle \beta, \alpha \rangle}{\langle \alpha, \alpha \rangle} $$ は整数となる.
$s_\alpha \cdot \alpha = -\alpha$ であることから,$\alpha \in R$ なら $-\alpha \in R$ も成り立つことに注意.対称空間の理論では,条件1, 3, 4は満たすが条件2を満たさない系が現れる.これらは「非縮退ルート系」と呼ばれる.コクセター群の理論では,条件1, 2, 3は満たすが条件4を満たさない系が現れる.これらは「非結晶型」または「非整数型ルート系」と呼ばれる.ここでは,上の定義のすべての条件を満たすルート系のみを扱う.
写像 $s_\alpha$ は,$\alpha$ に直交する超平面についての反射である.すなわち,$s_\alpha \cdot \alpha = -\alpha$ となり,$\alpha$ に直交するすべての $\beta$ について $s_\alpha \cdot \beta = \beta$ となることは,$s_\alpha$ の定義式から容易に分かる.このことから,$s_\alpha$ は $E$ 上の直交変換であり,行列式は $-1$ となることが明らかである.
性質4は幾何学的に2通りに解釈できる.$s_{\alpha}$の定義式を考えると,性質4は「$s_{\alpha} \cdot \beta$が$\beta$と$\alpha$の整数倍だけ異なる」ことと同値である.あるいは,$\beta$の$\alpha$への直交射影が $$ \frac{\langle \beta, \alpha \rangle}{\langle \alpha, \alpha \rangle} \alpha $$ で与えられることを思い出すと,性質4の量はこの射影における$\alpha$の係数の2倍である.したがって,性質4は「$\beta$の$\alpha$への射影が$\alpha$の整数倍または半整数倍になる」ことと同値である.
すべての複素半単純Lie代数にはルート系を対応させることができることを示した.実は,すべてのルート系はこの方法で得られる.ただし,これは自明ではない.
Weyl群
$(E, R)$ がルート系であるとき,ルート系 $R$ の Weyl 群 $W$ とは,$E$ の直交群の部分群で,すべての反射 $s_\alpha$($\alpha \in R$)によって生成される群である.
仮定より,各 $s_\alpha$ は $R$ を $R$ 自身へ写す(実際,全射である).なぜなら,任意の $\beta \in R$ について $\beta = s_\alpha(s_\alpha(\beta))$ が成り立つからである.したがって,Weyl群の任意の元は $R$ を $R$ へ写すことになる. ルートは $E$ を張るので,$E$ の線型変換は $R$ 上での作用によって決定される.よって,Weyl群は $O(E)$ の有限部分群であり,$R$ 上の置換群の部分群とみなすことができる.$w \in W$ の $H \in E$ への作用は $w \cdot H$ で表す.
ルート系の直和
$(E, R)$と$(F, S)$がルート系であるとする.ベクトル空間$E \oplus F$を,$E$と$F$上の内積から自然に定まる内積で考える.このとき,$R \cup S$は$E \oplus F$内のルート系となり,これを$R$と$S$の直和と呼ぶ.
ここで,$E$ を $E \oplus F$ の部分空間(すべてのベクトルが $(e, 0)$ の形,$e \in E$)と同一視し,$F$ も同様に $(0, f)$ の形($f \in F$)で同一視している.したがって,より厳密には $R \cup S$ とは,$R$ の元 $(\alpha, 0)$ と $S$ の元 $(0, \beta)$ の集合を意味する($R$ の $\alpha$ と $S$ の $\beta$ の両方を持つ $(\alpha, \beta)$ の形の要素は $R \cup S$ には含まれない).
既約ルート系
ルート系 $(E, R)$ が可約であるとは,$E$ が直交する非零部分空間 $E_1$ と $E_2$ の直和 $E = E_1 \oplus E_2$($\dim E_1 > 0$, $\dim E_2 > 0$)として分解できて,$R$ のすべての元が $E_1$ または $E_2$ のいずれかに属する場合をいう.このような分解が存在しない場合,$(E, R)$ は既約であるという.
ルート系 $(E, R)$ が可約である場合,$R$ の $E_1$ に属する部分は $E_1$ のルート系となり,$R$ の $E_2$ に属する部分は $E_2$ のルート系となることは容易に分かる.したがって,ルート系が可約であるとは,2つのルート系の直和として実現できる場合に限る.Lie代数の文脈では,複素半単純Lie代数 $\mathfrak{g}$ に対応するルート系が既約であることと,$\mathfrak{g}$ が単純であることは同値である.
同型なルート系
2つのルート系 $(E, R)$ と $(F, S)$ が同型であるとは,$E$ から $F$ への可逆線型変換 $A$ が存在し,$A$ が $R$ を $S$ へ写し,すべての $\alpha \in R$ および $\beta \in E$ について $$ A(s_{\alpha}\cdot\beta)=s_{A\alpha}\cdot(A\beta) $$ が成り立つ場合をいう.このような写像 $A$ を同型写像と呼ぶ.
線型写像 $A$ は内積を保つ必要はなく,ルートに関する反射を保つだけでよいことに注意.例えば,$F = E$ で $S$ が $R$ の各元の $c$ 倍($c \in \mathbb{R}$)からなる場合,$(F, S)$ は $(E, R)$ と同型であり,その同型写像は $A = cI$ で与えられる.
ここで,ルート系に現れる可能な角度や長さの比を制限する基本的な結果を示す.
ルートの角度
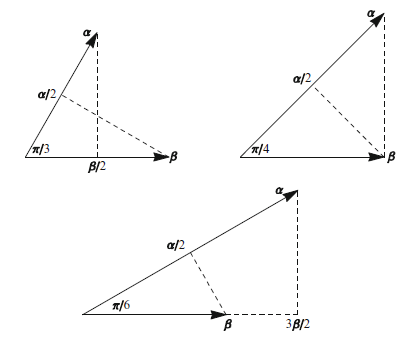
$\alpha$と$\beta$がルートであり,$\alpha$が$\beta$の倍数でなく,$\langle \alpha, \alpha \rangle \geq \langle \beta, \beta \rangle$であるとする.このとき,次のいずれかが成り立つ:
- $\langle \alpha, \beta \rangle = 0$
- $\langle \alpha, \alpha \rangle = \langle \beta, \beta \rangle$ かつ $\alpha$と$\beta$のなす角は$\pi/3$または$2\pi/3$
- $\langle \alpha, \alpha \rangle = 2\langle \beta, \beta \rangle$ かつ $\alpha$と$\beta$のなす角は$\pi/4$または$3\pi/4$
- $\langle \alpha, \alpha \rangle = 3\langle \beta, \beta \rangle$ かつ $\alpha$と$\beta$のなす角は$\pi/6$または$5\pi/6$
下図は,鋭角の場合に許される角度と長さの比を示している.いずれの場合も,$2\langle \alpha, \beta \rangle / \langle \alpha, \alpha \rangle = 1$ となるが,$2\langle \beta, \alpha \rangle / \langle \beta, \beta \rangle$ はそれぞれ 1, 2, 3 の値をとる.後で許される各角度と長さの比が,実際にあるルート系で現れることを示す.
有限なルート系
$\alpha$と$\beta$がルートであるとする.$\alpha$と$\beta$のなす角が鈍角(すなわち$\pi/2$より大きく$\pi$より小さい)であれば,$\alpha+\beta$もルートである.$\alpha$と$\beta$のなす角が鋭角(すなわち0より大きく$\pi/2$より小さい)であれば,$\alpha-\beta$および$\beta-\alpha$もルートである.
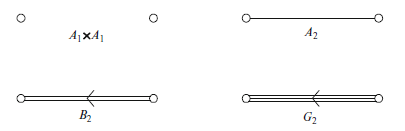
ルート系の階数が1の場合,可能性はただひとつしかない:$R$は$E$の非零元に対して,そのペア$\{\pm\alpha\}$のみからなる必要がある.階数が2の場合,可能性は4つあり,慣例的な名称とともに下図に示されている.$A_1 \oplus A_1$の場合,水平なルートの長さは垂直なルートの長さとは無関係である.$A_2$ではすべてのルートが同じ長さを持つ.$B_2$では長いルートの長さは短いルートの$\sqrt{2}$倍,$G_2$では長いルートの長さは短いルートの$\sqrt{3}$倍となる.隣り合うルートのなす角は$A_1 \oplus A_1$では$\pi/2$,$A_2$では$\pi/3$,$B_2$では$\pi/4$,$G_2$では$\pi/6$である.これらの系が実際にルート系であることは容易に確かめられる.特に,各ルートのペアについて満たされている.
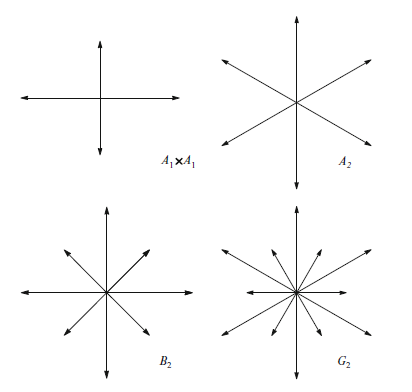
階数2のルート系
階数2のすべてのルート系は,上図に示したいずれかのルート系と同型である.
以前の結果を用いると,ルート系$A_1\times A_1$,$A_2$,$B_2$が古典的Lie代数のルート系として現れることが分かる.ルート系$A_1\times A_1$は$\mathfrak{so}(4,\mathbb{C})$のルート系であり,これは$\mathfrak{sl}(2,\mathbb{C}) \oplus \mathfrak{sl}(2,\mathbb{C})$と同型である.$A_2$は$\mathfrak{sl}(3,\mathbb{C})$のルート系であり,$B_2$は$\mathfrak{so}(5,\mathbb{C})$のルート系であり,これは$\mathfrak{sp}(2,\mathbb{C})$のルート系とも同型である.一方,$G_2$のルート系は「例外的」Lie代数($G_2$とも呼ばれる)のルート系である.
階数2のルート系のWeyl群
$R$ が階数2のルート系であり,最小角が $2\pi/n$($n=4,6,8,12$)であれば,$R$ の Weyl 群は正 $n/2$ 角形の対称群となる.
$A_2$の場合,Weyl群は3つの反射と3つの回転($2\pi/3$の整数倍の回転)から構成されることに注意.この場合,Weyl群はルート系の全対称群ではない:$R$を$2\pi/3$回転しても$R$自身に写るが,これらの回転はWeyl群の元ではない.
ここで,ルート系に対する重要な双対操作を導入する.
双対ルート系
$(E, R)$ がルート系であるとき,各ルート $\alpha \in R$ に対して,コルート $H_\alpha$ は $$ H_{\alpha}=2\frac{\alpha}{\langle \alpha, \alpha \rangle} $$ で定義される.すべてのコルートの集合を $R^\vee$ と書き,$R$ の双対ルート系と呼ぶ.
この定義は前に定義した「コルート」という用語を使う場合と一致している.ルート系の定義の4番目の条件は,「すべてのルート$\alpha$と$\beta$について,$\langle \beta, H_\alpha \rangle$が整数になるべきである」と言い換えることができる.
双対ルート系の性質
$R$ がルート系であれば,その双対 $R^\vee$ もルート系であり,$R^\vee$ の Weyl 群は $R$ の Weyl 群と一致する.さらに,$R^\vee$ の双対は $R$ となる.
双対ルート系 $R^\vee$ におけるペア $(H_\alpha, H_\beta)$ に対応する整数は,元のルート系 $R$ におけるペア $(\beta, \alpha)$($(\alpha, \beta)$ではなく)に対応する整数と一致することに注意.$R$ のすべてのルートが同じ長さを持つ場合,$R^\vee$ は $R$ と同型になる.すべてのルートが同じ長さでなくても,$R$ と $R^\vee$ が同型になる場合もある.例えば $B_2$ の場合,双対ルート系 $R^\vee$ は $\pi/4$ 回転とスケーリングによって $R$ に戻すことができる(下図参照).一方,階数 3 のルート系 $B_3$ と $C_3$は互いに双対だが,同型ではない.
上図は,ルート系$B_2$の双対ルート系を示している.図の左側では,長いルートの長さが$\sqrt{2}$になるように規格化されている.したがって,各長いルートについては$H_\alpha = \alpha$,各短いルートについては$H_\alpha = 2\alpha$となり,右側の双対ルート系が得られる.
ここで,ルート系の「基底」または「正単純ルート系」という概念を導入する.
基底
$(E, R)$ がルート系であるとき,$R$ の部分集合 $\Delta$ が基底であるとは,次の条件を満たす場合をいう:
- $\Delta$ は $E$ のベクトル空間としての基底である.
- 任意のルート $\alpha \in R$ は,$\Delta$ の元の整数係数による線型結合として表せて,かつその係数はすべて非負か,すべて非正のいずれかである.
注意すべきは,$\Delta$が$E$の基底であるため,各$\alpha$は$\Delta$の元の線型結合として一意的に表せることである.$\Delta$は,各$\alpha \in R$の展開係数が整数であり,かつ非零係数の符号がすべて同じになるように選ばれていることを要求する.
基底の内積と非正性
基底$\Delta$の異なる2つの要素 $\alpha, \beta$ に対して, $R$ の基底であれば, $\langle \alpha, \beta \rangle \leq 0$ が成り立つ.
幾何学的には,これは $\alpha$ と $\beta$ が直交しているか,または両者のなす角が鈍角であることを意味する.
ここで,すべてのルート系が基底を持つことを示す.
ルートを含まない超平面の存在
原点を通り,$R$のいずれの要素も含まない超平面$V$が$E$内に存在する.
分解
$(E, R)$ をルート系とする.$V$ を $E$ 内の原点を通る超平面で,$V$ がいかなるルートも含まないとする.$V$ の一方の「側」を選び,$R^C$ をこの側にあるルート全体の集合とする.$R^C$ の元 $\alpha$ が分解可能であるとは,$R^C$ の元 $\beta, \gamma$ が存在して $\alpha = \beta + \gamma$ となる場合をいう.そのような元が存在しない場合,$\alpha$ は分解不可能であるという.
$V$ の「側」は,$E \setminus V$ の連結成分として定義できる.あるいは,$V$ に直交する非零ベクトル $H$ を取ると,$V$ は $E$ の元 $\mu$ で $\langle \mu, H \rangle = 0$ を満たすもの全体の集合となる.このとき,$V$ の2つの「側」は,それぞれ $\langle \mu, H \rangle > 0$ を満たす $\mu \in E$ の集合と,$\langle \mu, H \rangle < 0$ を満たす $\mu \in E$ の集合である.
ルート系の基底の存在
$(E, R)$ をルート系とし,$V$ を $E$ 内の原点を通る超平面で,$V$ が $R$ のいかなる要素も含まないとする.また,$R^C$ を $V$ の一方の側にあるルート全体の集合とする.このとき,$R^C$ の分解不可能な要素全体の集合は $R$ の基底となる.
この基底の構成は,「正単純ルート」という用語の動機付けとなる.まず,正ルート($R^C$)を$V$の一方の側にあるルートとして定義し,次に正単純ルート(基底)を$R^C$の分解不可能(または「単純」)な要素の集合として定義する.
下図は上の定理を$G_2$のルート系の場合で示している.破線の一方の側にある分解不可能なルート$\alpha_1$と$\alpha_2$が描かれている.
ルート系の基底に対応する超平面の存在
任意のルート系 $R$ の基底に対して,超平面 $V$ とその一方の側が存在し,その基底は上の定理の方法で得られる.
双対ルート系の基底
$\Delta$が$R$の基底であれば,すべてのコルート$H_\alpha$($\alpha \in \Delta$)からなる集合は双対ルート系$R^\vee$の基底となる.
下図は,上の命題をルート系$B_2$の場合で示している.
Weylチャンバー
ルート系 $(E, R)$ の開Weylチャンバーとは, $$ E - \bigcup_{\alpha \in R} V_\alpha $$ の連結成分である.ここで,$V_\alpha$ は原点を通り $\alpha$ に直交する超平面である. $\Delta = \{\alpha_1, \ldots, \alpha_r\}$ が $R$ の基底であれば,$E$ 内の開基本Weylチャンバー($\Delta$に関する)は, $H \in E$ で $$ \langle \alpha_j, H \rangle > 0 \quad (j = 1, \ldots, r) $$ を満たすもの全体の集合である.
下図は,$A_2$ルート系のある基底に対応する開基本Weylチャンバー$C$を示している.$C$の境界は,ルートに直交する直線(ルートを通る直線ではない)の部分から構成されていることに注意.
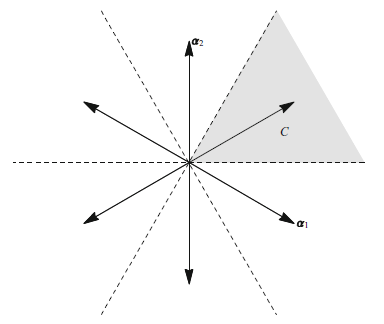
基底の要素はベクトル空間として $E$ の基底を成すので,初等線型代数から,開基本 Weyl チャンバーは凸であり,したがって連結かつ空でないことが分かる.基本 Weyl チャンバーから出る唯一の方法は,ある点 $H$ で $$ \langle \alpha_j, H \rangle = 0 $$ となる超平面を通過することであるため,開基本 Weyl チャンバーは確かに開 Weyl チャンバーとなる.また,すべての $j=1,\ldots,r$ について $\langle \alpha_j, H \rangle > 0$ ならば,すべての $\alpha \in R^+$ についても $\langle \alpha, H \rangle > 0$ となる.なぜなら,$\alpha$ は $\alpha_1, \ldots, \alpha_r$ の非負係数による線型結合だからである.
各 $w \in W$ は $R$ を $R$ へ写す直交線型変換であり,したがってルートに直交する超平面の集合も自身へ写す.このことから,任意の開Weylチャンバー $C$ に対して,$w \cdot C$ も別の開Weylチャンバーとなることが容易に分かる.
任意の基底とそれに対応する正ルート集合 $R^C$ に対し,基本Weylチャンバーは,各基底要素および各正ルートとの内積が正となる元全体の集合として定義した.次の結果は,この定義を逆にたどることができることを述べている.
Weylチャンバーと基底の関係
任意の開Weylチャンバー $C$ に対して,$R$ の基底 $\Delta_C$ が一意に存在し,$C$ はその基底に対応する開基本Weylチャンバーとなる.$\Delta_C$ に関する正ルートは,$C$ のすべての要素との内積が正となる $R$ の元全体である.
したがって,基底とWeylチャンバーの間には一対一対応が存在する.
すべてのルートはある基底の要素
すべてのルートは,ある基底の要素である.
$C$ は,すべての $j = 1,\ldots, r$ について $\langle \alpha_j, H \rangle > 0$ を満たす $H \in E$ の集合なので,$C$ の境界の余次元 1 の部分は,基底要素 $\alpha_j$ に直交する超平面 $V_{\alpha_j}$ の部分から構成される.したがって,この命題を証明するには,すべてのルート $\alpha$ について,超平面 $V_\alpha$ がある $C$ の境界の余次元 1 の部分を含むことを示せばよい.
Weyl群の作用とWeylチャンバーの関係について,いくつかの結果を確立する.
Weyl群とWeylチャンバー
Weyl群は開Weylチャンバーの集合上に推移的に作用する.
Weyl群の生成
$\Delta$が基底であれば,Weyl群$W$はすべての$s_\alpha$($\alpha \in \Delta$)によって生成される.
Weylチャンバーの閉包
$C$ を Weyl チャンバーとし,$H, H'$ を $\overline{C}$($C$ の閉包)の元とする.もしある $w \in W$ について $w \cdot H = H'$ となるなら,$H = H'$ である.
すなわち,$C$ の異なる2つの元は,Weyl群 $W$ の同じ軌道に入ることはない.
上の命題より,任意の $w \in W$ は基底 $\Delta$ に対応する反射の積として書くことができる. $k \geq 0$ を,$w$ を $\Delta$ の反射 $k$ 個の積として表すのに必要な最小の数とする.このとき,$w$ を $\Delta$ の反射 $k$ 個の積として表す任意の表現を,$w$ の「最小表現」と呼ぶ.最小表現は一意とは限らない.
Weyl群の作用とWeylチャンバー
Weyl群は開Weylチャンバーの集合上に自由に作用する.すなわち,$H$がある開チャンバー$C$に属し,ある$w \in W$について$w \cdot H = H$となるなら,$w$は恒等変換$I$である.
Weyl群の作用の一意性
$R$の任意の2つの基底$\Delta_1$と$\Delta_2$に対して,$w \in W$が一意に存在し,$w \cdot \Delta_1 = \Delta_2$となる.
Weylチャンバーと$W$-軌道
$C$ を Weyl チャンバー,$H$ を $E$ の元とする.このとき,$H$ の $W$-軌道には,$C$ の閉包 $\overline{C}$ に含まれる点がちょうど1つだけ存在する.
ここで主張しているのは,「$w$ が一意に存在して $w \cdot H \in C_N$ となる」ということではなく,「$C_N$ の中に一意な点 $H_0$ が存在し,$H_0$ は(必ずしも一意とは限らないが)$H_0 = w \cdot H$ の形で表せる」ということである.
基底の置換
$\Delta$を$R$の基底とし,$R^+$をそれに対応する正ルートの集合とする.$\alpha \in \Delta$を取る.$\beta \in R^+$で$\beta \neq \alpha$ならば,$s_\alpha \cdot \beta \in R^+$が成り立つ.すなわち,$\alpha \in \Delta$なら,$s_\alpha$は$\alpha$以外の正ルートを置換する.
Dynkin図は,ルート系$R$の基底の構造,ひいては$R$自体の構造を符号化する便利なグラフィカルな方法である.
Dynkin図
$\Delta = \{\alpha_1, \ldots, \alpha_r\}$ がルート系 $R$ の基底であれば,Dynkin図は $r$ 個の頂点 $v_1, \ldots, v_r$ からなるグラフである.異なる2つの頂点 $v_j$ と $v_k$ の間には,$\alpha_j$ と $\alpha_k$ のなす角が $\pi/2, 2\pi/3, 3\pi/4, 5\pi/6$ のいずれかの場合に応じて,それぞれ0本,1本,2本,3本の辺を引く.さらに,$\alpha_j$ と $\alpha_k$ が直交しておらず,長さが異なる場合,$v_j$ と $v_k$ の間の辺には,長いルートに対応する頂点から短いルートに対応する頂点へ向かう矢印を付ける.
上の命題より,角度が $2\pi/3$, $3\pi/4$, $5\pi/6$ の場合,ルートの長さの比(長い方/短い方)はそれぞれ $1$, $\sqrt{2}$, $\sqrt{3}$ となることに注意.したがって,2つの非直交なルートに対応する頂点間の辺の本数は,長さの比が $1$, $\sqrt{2}$, $\sqrt{3}$ の場合に応じてそれぞれ 1本,2本,3本となる.辺に付ける矢印は「大なり」記号のように考えると,どちら向きに矢印を付けるべきか覚えやすい.
2つのDynkin図が同型であるとは,一方の頂点から他方の頂点への一対一かつ全射の対応が存在し,その対応が辺の本数と矢印の向きを保つ場合をいう.上の命題より,固定したルート系に対する任意の2つの基底$\Delta_1$と$\Delta_2$は,一意なWeyl群の元$w$によって関連付けられる.$w$は角度と長さを保つので,同じルート系に対する異なる基底から得られるDynkin図は同型となる.
例えばルート系 $G_2$ の場合,基底は長さ比が $\sqrt{3}$ で,なす角が $5\pi/6$ の2つのルートからなる.したがって,Dynkin図は2つの頂点が3本の辺で結ばれ,長いルート($\alpha_2$)から短いルート($\alpha_1$)へ矢印が付く形になる.最後に,$A_1 \oplus A_1$ の場合,基底の2つの要素は直交しているので,下図のような結果となる.
Dynkin図の性質
- ルート系が既約であることと,そのDynkin図が連結であることは同値である.
- 2つのルート系$R_1$と$R_2$のDynkin図が同型であれば,$R_1$と$R_2$自体も同型である.
Dynkin図と単純Lie代数
$\mathfrak{g} = \mathfrak{k}_{\mathbb{C}}$ を半単純Lie代数,$\mathfrak{h} = \mathfrak{t}_{\mathbb{C}}$ をそのCartan部分代数,$R \subset i\mathfrak{t}$ を $\mathfrak{g}$ のルート系とする.このとき,$\mathfrak{g}$ が単純であることと,$R$ のDynkin図が連結であることは同値である.
半単純Lie代数の表現
この節では,複素半単純Lie代数$\mathfrak{g}$の既約有限次元表現に対する最高ウェイト定理を証明する.まず,すべての既約有限次元表現が最高ウェイトを持つこと,同じ最高ウェイトを持つ2つの既約表現は同型であること,既約表現の最高ウェイトはdominantな整数元でなければならないことを示す.これらは以前の$\mathfrak{sl}(3,\mathbb{C})$の場合と全く同じ方法で証明できる.残るは,任意のdominantな整数元が実際に何らかの既約表現の最高ウェイトとなることを示すことである.$\mathfrak{sl}(3,\mathbb{C})$の場合は,まず基本ウェイト$(1,0)$と$(0,1)$を最高ウェイトとする表現を構成し,それらのテンソル積を取ることで任意の最高ウェイトの表現を得た.しかし,一般の半単純Lie代数$\mathfrak{g}$の場合,基本ウェイトを最高ウェイトとする表現を簡単に構成する方法は存在しない.したがって,与えられたdominantな整数元を最高ウェイトとする既約表現を構成する新しい方法が必要となる.この構成がこの節の主題である.
次節では,既約表現のウェイト集合の構造,ウェイトの重複度,表現の次元など,いくつかの追加的な性質を導出する.またその節では,$\mathfrak{g}$の表現の完全可約性,すなわち任意の有限次元表現が既約表現の直和として分解できることも示す.
この節全体を通して,$\mathfrak{g} = \mathfrak{k}_{\mathbb{C}}$ を複素半単純Lie代数,$\mathfrak{h} = \mathfrak{t}_{\mathbb{C}}$ を$\mathfrak{g}$の固定したCartan部分代数と仮定する.$\mathfrak{g}$上には,$\mathfrak{k}$上で実数値をとり,$\mathfrak{k}$の随伴作用に関して不変な内積を固定する.$R \subset i\mathfrak{t}$ を$\mathfrak{g}$のCartan部分代数$\mathfrak{h}$に関するルート集合とし,$\Delta$を$R$の固定した基底とする.また,$\Delta$に関して正ルート全体の集合を$R^+$,負ルート全体の集合を$R^-$とする.各ルート$\alpha$に対して,コルート$H_\alpha \in \mathfrak{h}$を $$ H_{\alpha}=2\frac{\alpha}{\langle \alpha, \alpha \rangle} $$ で定める.さらに,Weyl群$W$,すなわちルートに直交する超平面に関する反射で生成される$\mathfrak{h}$上の線型変換の群を考える.最後に,整数元およびdominantな整数元の概念も考える.
ここで,$\mathfrak{sl}(3,\mathbb{C})$の場合と同様に,表現のウェイトの概念を導入する.
ウェイト
$(\pi,V)$が$\mathfrak{g}$の表現(無限次元でもよい)であるとする.$\lambda \in \mathfrak{h}$が$\pi$のウェイトであるとは,ある非零ベクトル$v \in V$が存在して,すべての$H \in \mathfrak{h}$について $$ \pi(H)v = \langle \lambda, H \rangle v $$ を満たす場合をいう.ウェイト$\lambda$に対応するウェイト空間は,この条件を満たすすべての$v \in V$の集合であり,ウェイトの重複度は対応するウェイト空間の次元である.
この節全体を通して,異なるウェイトを持つウェイトベクトルは線型独立であるという事実を断りなく使用する.
有限次元表現のウェイト
$\mathfrak{g}$の有限次元表現$(\pi, V)$において,すべてのウェイトは整数元である.
ウェイトに対するWeyl群の作用
$\mathfrak{g}$の有限次元表現$(\pi, V)$に対して,ウェイトとその重複度は,$\mathfrak{h}$上のWeyl群$W$の作用で不変である.
「最高ウェイト定理」の「簡単な部分」を述べる:
最高ウェイトの存在
- $\mathfrak{g}$の任意の既約有限次元表現は最高ウェイトを持つ.
- $\mathfrak{g}$の2つの既約有限次元表現が同じ最高ウェイトを持つなら,それらは同型である.
- $(\pi, V)$が$\mathfrak{g}$の既約有限次元表現で最高ウェイト$\mu$を持つなら,$\mu$はdominantな整数元である.
ここで,最高ウェイト定理の「難しい部分」に進む.
最高ウェイトに対応する有限次元既約表現
$\mu$がdominantな整数元であれば,$\mathfrak{g}$の最高ウェイトが$\mu$である既約有限次元表現が存在する.
先に述べたように,$\mathfrak{sl}(3,\mathbb{C})$の場合の証明方法は,一般の半単純Lie代数には容易に拡張できない.
目標は,各dominantな整数元$\mu \in \mathfrak{h}$に対して,最高ウェイトが$\mu$である有限次元既約表現を$\mathfrak{g}$上に構成することである.この構成は2段階で進める.第1段階では,$\mathfrak{g}$の無限次元表現$V_\mu$(Verma加群と呼ばれる)を構成する.この表現は既約ではないが,最高ウェイト$\mu$を持つ巡回表現となる.$V_\mu$は,$\mathfrak{g}$のいわゆる普遍包絡代数$U(\mathfrak{g})$の商として構成する.$V_\mu$内の最高ウェイトベクトルがゼロでないことを示すために,$U(\mathfrak{g})$の構造定理(Poincaré-Birkhoff-Witt定理)を用いる必要がある.$\mathfrak{g}$の有限次元表現とは異なり,Verma加群のウェイトはWeyl群の作用で不変ではない.
構成の第2段階では,$\mu$がdominantな整数元であるとき,$V_\mu$には不変部分空間$W_\mu$が存在し,商空間$V_\mu/W_\mu$は有限次元かつ既約で,しかもゼロではないことを示す.この商空間が有限次元であることを示すために,$\mu$がdominantな整数元であれば,$V_\mu/W_\mu$のウェイト($V_\mu$のウェイトとは異なり)はWeyl群の作用で不変になることを証明する.したがって,$V_\mu/W_\mu$の各ウェイト$\lambda$は整数元であり,すべてのWeyl群の元$w$について$w \cdot \lambda \preceq \mu$を満たす.この性質を持つ$\lambda$は有限個しか存在しないことが分かる.また,各ウェイト$\lambda$の重複度は($V_\mu$の場合でも)有限なので,$V_\mu/W_\mu$は有限次元となる.
最高ウェイト巡回的
(無限次元でもよい)表現 $(\pi, V)$ が$\mathfrak{g}$の最高ウェイト巡回的であり,最高ウェイト$\mu \in \mathfrak{h}$を持つとは,$V$に非零ベクトル$v$が存在して,次の条件を満たす場合をいう:
- すべての$H \in \mathfrak{h}$について$\pi(H)v = \langle \mu, H \rangle v$が成り立つ.
- すべての正ルート$\alpha \in R^+$に対して,$X \in \mathfrak{g}_\alpha$なら$\pi(X)v = 0$が成り立つ.
- $v$を含む最小の不変部分空間が$V$全体となる.
$\mu\in\mathfrak{h}$が整数である必要はないことに注意.すべての有限次元の最高ウェイト巡回表現は既約となるが,無限次元の場合はそうではない.また,最高ウェイトが同じ2つの最高ウェイト巡回表現が同型になるとは限らず,両方が有限次元の場合のみ同型となる.この節では,任意の$\mu \in \mathfrak{h}$に対して,最高ウェイト$\mu$を持つ特定の最高ウェイト巡回表現$V_\mu$(Verma加群として知られる)を構成する.Verma加群は,ある最高ウェイトに対する「最大の」最高ウェイト巡回表現であり,$\mu$がdominantな整数元であっても常に無限次元となる.
$\mathfrak{sl}(2,\mathbb{C})$の場合,Verma加群は次のように明示的に構成できる.任意の複素数$\mu$に対して,無限次元ベクトル空間$V_\mu$を,基底$v_0, v_1, v_2, \ldots$で定義する($V_\mu$の元は$v_j$の有限線型結合である).$\mathfrak{sl}(2,\mathbb{C})$の作用を,次の式で定める: \begin{align} \pi_{\mu}(Y)v_j =& v_{j+1} \\ \pi_{\mu}(H)v_j =& (\mu-2j)v_j \\ \pi_{\mu}(X)v_0 =& 0 \\ \pi_{\mu}(X)v_j =& j(\mu-(j-1))v_{j-1} \end{align} 以前は,$v_j$は$j$が十分大きいとゼロになったが,ここでは$v_j$は定義によりすべて線型独立であることに注意.直接計算により,これらの式が$\mathfrak{sl}(2,\mathbb{C})$の表現を定義していることが分かる.
$\mu$ が非負整数 $m$ の場合,$v_m, v_{m+1}, v_{m+2}, \ldots$ で張られる空間 $W_\mu$ は $\mathfrak{sl}(2,\mathbb{C})$ の作用で不変となる.実際,$W_\mu$ は明らかに $\pi_\mu(Y)$ および $\pi_\mu(H)$ の作用で不変であり,$\pi_\mu(X)$ の作用についても,$\mu = m$ のとき $$ \pi_\mu(X)v_{m+1} = (m - m) v_m = 0 $$ となるので不変である.したがって,$W_\mu$ は不変部分空間となり,商空間 $V_\mu / W_\mu$ には自然に $\mathfrak{sl}(2,\mathbb{C})$ の作用が誘導される.この商空間が,最高ウェイト $\mu$ を持つ $\mathfrak{sl}(2,\mathbb{C})$ の有限次元既約表現となる.
一般の半単純Lie代数$\mathfrak{g}$の場合も同様のことを行いたい.基底 $$ Y_1,\ldots,Y_N,H_1,\ldots,H_r,X_1,\ldots,X_N $$ を選ぶ.$V_\mu$が最高ウェイト$\mu$を持つ最高ウェイト巡回表現で,最高ウェイトベクトルを$v_0$とする.このとき,$V_\mu$は,この基底要素を$v_0$に作用させた積で張られる.順序交換補題により,任意の積は順序に並べ替えた項の線型結合として書ける.この順序に並べた場合,$X_j$を含む項は$v_0$に作用させると必ずゼロになる.また,$X_j$を含まない項では,$H_k$の因子は$v_0$に作用させると$\mu(H_j)$を与えるだけである.したがって,$V_\mu$は $$ \pi_{\mu}(Y_1)^{n_1}\pi_{\mu}(Y_2)^{n_2}\cdots\pi_{\mu}(Y_N)^{n_N}v_0 $$ の形の要素で張られる.
Verma加群の考え方は,$\mathfrak{sl}(2,\mathbb{C})$の場合と同様に,上式のベクトルがVerma加群の基底を成すと「宣言」することである.Verma加群のウェイトは,すべて $$ \mu - n_1\alpha_1 - \cdots - n_N\alpha_N $$ の形(各$n_j$は非負整数)となる(下図参照).このように定めれば,Lie代数$\mathfrak{g}$の作用の仕方は一意に決まる.実際,Lie代数の元$Z$を先のベクトルに作用させると,前段落のように要素を並べ替えて順序通りにできる.すでに述べたように,$X_j$の因子はゼロになり,$H_k$の因子は定数を与えるだけである.したがって,最終的には上の式の形の要素の線型結合に戻ることになる.
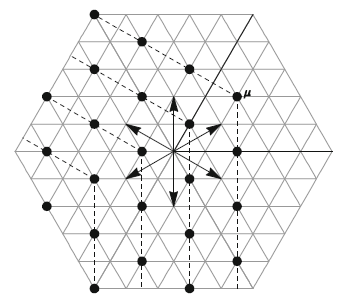
上記のVerma加群の記述における困難は,実際に上式のベクトルが$\mathfrak{g}$の表現の基底となることを直接確かめる合理的な方法がないことである.実際,$\mathfrak{g} = \mathfrak{sl}(2,\mathbb{C})$の場合を除き,各基底要素がどのように作用するかを明示的に記述することは不可能であり,したがってこれらの要素が正しい交換関係を満たすことを直接検証することもできない.それでも,後で上式のベクトルを基底とし,上記の方法で$\mathfrak{g}$が作用するようなwell-definedな表現が存在することを証明する.$\mu$がdominantな整数元の場合には,Verma加群の不変部分空間を構成し,その商空間が有限次元かつ既約となることも示す.