インフレーション

参考文献：E. W. Kolb, M. S. Turner, "The Early Universe", CRC Press, 2018.

標準的なビッグバン宇宙論は非常に成功している．これは，少なくとも軽元素合成の時代（$t \simeq 10^{-2}~10^{2}$ sec，$T \simeq 10~0.1$ MeV）から今日（$t \simeq 15$ Gyr，$T \simeq 2.75$ K）までの宇宙の歴史を，信頼できる検証済みの形で説明している．さらに，宇宙の最も初期の歴史を議論するための合理的な枠組みも提供している．現在，このシンプルで非常に洗練された宇宙の記述と矛盾する観測的・実験的データは存在しない．標準宇宙論は，低エネルギー素粒子物理学の標準模型，すなわち強い・弱い・電磁相互作用の$SU(3)\otimes SU(2)\otimes U(1)$ゲージ理論に匹敵する大きな成果である．

素粒子物理学の標準模型と同様に，標準宇宙論にもいくつかの未解決の問題が存在する．これらの問題はビッグバンモデル自体の矛盾ではなく，その成功ゆえに新たに問いかけることができるようになった疑問である．しかし，標準宇宙論はこれらの問いにまだ答えを与えていない．標準宇宙論が提起する宇宙論的な謎は，モデルが説明できるものの，その根本的な起源をまだ明らかにできていない，いくつかの非常に基本的な宇宙論的事実に関わっている．

目次

• 標準宇宙論の問題
• インフレーション：基本的な描像
• スカラー場のダイナミクスとしてのインフレーション
• 密度揺らぎと残存重力子
• 特定のインフレーションモデル
• 宇宙無毛定理
• インフレーション理論の検証
• インフレーションモデルの要約

標準宇宙論の問題

• Large-Scale Smoothness

  Robertson-Walker計量は，空間が一様かつ等方的であることを記述している．しかし，なぜ空間が一様かつ等方的なのかという疑問が残る．他にも，一様だが異方的な空間や，不均一な空間などの可能性がある．さらに，Einstein方程式の最も一般的な宇宙論的解は，等方的でも一様でもない．Robertson-Walker時空は非常に特別なものである．宇宙の滑らかさを最も正確に示しているのは宇宙マイクロ波背景放射（CMBR）であり，これは10秒角から180度の角度スケールで約1万分の1の精度で一様である．もし宇宙が非常に不均一であったり，膨張が異方的であったなら，CMBRにも同程度の温度異方性が存在するはずである．

  もし観測可能な宇宙全体が，宇宙マイクロ波背景放射（CMBR）が最後に散乱した時点で因果的に接触していたならば，Compton散乱のような微視的な物理過程によって温度の揺らぎが平滑化され，単一の温度が実現したと考えられるかもしれない．しかし，標準宇宙論の枠組みでは，粒子地平線が存在するため，これは起こり得なかった[1]．ある時代における粒子地平線の大きさは，地平線体積内のエントロピーで表すのが便利である： $$ S_{\text{HOR}}=s\frac{4\pi}{3}t^3\simeq \begin{cases} 0.05g_*^{-1/2}(m_{\text{Pl}}/T)^3 & (t \lesssim t_{\text{EQ}}) \\ 3\times10^{87}(\Omega_0h^2)^{-3/2}(1+z)^{-3/2} & (t \gtrsim t_{\text{EQ}}) \end{cases} $$

  初期宇宙の地平線内に含まれるエントロピーは，現在（約$10^{88}$）よりもはるかに小さかったことに注意．CMBRの典型的な光子が最後に散乱した再結合の時点で，地平線内のエントロピーは約$10^{83}$であった．これは，現在のHubble体積が再結合時には約$10^{5}$個の因果的に切り離された領域から構成されていたことを意味し，したがって因果的な過程によって滑らかさが実現されたとは考えにくい．この事実は別の言い方もできる．再結合時のHubble距離（すなわち$H^{-1}(t_{rec})$）は，今日の「空」でわずか約0.8度の角度に対応するが，CMBRは「空」全体で一様である．

  さらに，原始元素合成の時点で地平線内に含まれるエントロピーは $S_H(t_{\text{nucleo}}) \simeq 10^{63}$ であり，これは現在のHubble体積に含まれるエントロピーのわずか $10^{-25}$ 程度であった．驚くべきことに，現在の地平線体積を構成する $10^{25}$ 個の因果的に独立した領域それぞれで，軽元素の合成はほぼ同一に進行したように見える[2]．

  標準宇宙論に関する最初の厄介な事実は，なぜ宇宙が非常に大きなスケールでこれほどまでに滑らかであるのか，物理的な説明が存在しないことである．これはしばしば「地平線問題」と呼ばれる．

• Small-Scale Inhomogeneity

  宇宙は大きなスケールでは非常に滑らかに見える一方で，より小さなスケールでは星，銀河，銀河団，ボイド，超銀河団など，1 Mpcよりはるかに小さいものから100 Mpc（あるいはそれ以上）に及ぶ多様な構造が存在している．標準宇宙論はこのような豊富な小さいスケール構造の起源を理解するための非常に優れた枠組みを提供している．宇宙が物質優勢となると，初期の小さな密度不均一性がJeans（重力）不安定性によって成長し，今日見られる多様な構造へと発展する．残された光子（CMB）はこの重力崩壊には関与しなかったが，初期の不均一性の化石的な記録として残っており，初期の密度ゆらぎが約$10^{-4}$程度より大きくなかったことを示している．今日これほど豊富な構造が存在するという事実は，標準宇宙論にとってもう一つの謎，すなわち「初期の不均一性の起源は何か？」という問いを投げかけている．

  密度の不均一性は通常，Fourier展開で表される： $$ \frac{\delta\rho(\vec{x})}{\rho}=(2\pi)^{-3}\int\delta_k\exp(-i\vec{k}\cdot\vec{x})d^3k $$ ここで，$\rho$は宇宙の平均密度，$\vec{k}$は各モードに対応する共動波数，$\delta_k$はその振幅である．密度摂動の振幅が小さい間（$\delta\rho/\rho \ll 1$），物理的な波数や波長は$R(t)$に比例して単純にスケールする：$k_{\text{phys}} = k / R(t)$，$\lambda_{\text{phys}} = R(t)(2\pi/k)$．多くの場合，$R(t)$は$R(\text{today}) = 1$となるように規格化され，このとき$\lambda_{\text{phys}} = \lambda$となる．摂動が非線形になると，一般的な膨張から分離し，ほぼ一定の物理的サイズを保つ．また，あるモードを，半径$\lambda/2$の球内に含まれる不変質量で記述することも便利である： $$ M(\lambda)\equiv\frac{\pi}{6}\lambda_{\text{phys}}^3\rho_{\text{NR}}\simeq1.5\times10^{11}(\Omega_0h^2)(\lambda/\text{Mpc})^3M_\odot $$ したがって，銀河質量の摂動は$\lambda_{\text{GAL}} \sim 1$ Mpcに対応する[3]．

  Gauss型ゆらぎの場合，摂動に関するすべての情報はパワースペクトルに含まれている．あるスケールでの不均一性の度合いを直感的に表す一般的な指標として，そのスケールでのrms（2乗平均平方根）質量ゆらぎがあり，これはパワースペクトルと次のような関係にある： \begin{align} \langle (\delta\rho/\rho)^2 \rangle_{\lambda} \equiv& V^{-1}\int d^3x \left[ \frac{\int d^3r W(r)\rho(\vec{x}+\vec{r})}{\int d^3r W(r)\rho(\vec{r})}-1 \right]^2 \\ =& V^{-1}(2\pi)^{-3}\int 4\pi k^2 dk |\delta_k|^2 |W(k)|^2/V_W^2 \\ \simeq& V^{-1}(k^3|\delta_k|^2/2\pi^2)_{k\sim 2\pi/\lambda} \end{align} ここで$W(r)$は特徴的なスケール$\lambda$をもつウィンドウ関数（例えば$r\ll\lambda$で$W(r)\simeq1$，$r\gg\lambda$で$W(r)\ll1$），$V_W=4\pi\int W(r)r^2dr$はウィンドウ関数で定義される体積，$V$は基本立方体の体積（密度場をFourier展開するため周期的境界条件を課す必要がある）である．

  密度ゆらぎの起源に関する明確なモデルが存在しない場合，通常，ゆらぎのスペクトルには特定のスケールがなく，すなわちパワーロー（べき乗則）であると仮定される．すなわち，$|\delta_k|^2 \propto k^n$ であり，これより $(\delta\rho/\rho)_\lambda \propto M^{-n/6-1/2}$ となる．

  後ほど見るように，密度ゆらぎのスペクトルを記述する非常に便利な方法は，各モードが地平線内に入るとき，すなわち物理的な波長がHubble半径に等しくなるとき（$\lambda_{\text{phys}} \sim H^{-1}$）の振幅を指定することである[4]．これは，地平線進入時やそれ以前であれば，Newtonポテンシャルのゆらぎ$(\delta\rho/\rho)_{\text{HOR}}$を特定できるため便利である．興味深いのは，いわゆるHarrison-Zel'dovichスペクトル（$n=-3$）であり，これは曲率ゆらぎが一定となるスペクトルである．この場合，$(\delta\rho/\rho)_{\text{HOR}}$は定数となる．このようなスペクトルは非常に単純で美しいだけでなく，長波長・短波長のいずれにおいても$(\delta\rho/\rho)_\lambda \gtrsim 1$とならないため，長波長モードによるCMBR温度ゆらぎの過剰や，短波長モードによるブラックホール生成の過剰を避けることができるという利点もある．

  構造形成の理論的理解はまだ十分ではなく，現在の観測から初期密度ゆらぎのスペクトルを決定することはできない．しかし，1 Mpcから10 Mpc程度のスケールで非線形構造が今日存在していること，そして線形領域のゆらぎは物質優勢期に$R(t)$に比例して成長することから，物質・放射等価の時代にこれらのスケールで$10^{-5}$程度の振幅の摂動が存在していたはずだと推測できる．現時点では，ダークマターの性質にも依存するが，観測される構造と整合的なスペクトルとして（Harrison-Zel'dovichスペクトルを含む）いくつかの候補が考えられると言える．

  放射優勢期において，現在非相対論的な粒子（バリオンやその他）が地平線内に含まれる質量は次式で与えられる： $$ M_{\text{HOR}}(t)\simeq0.29g_*^{-1/2}(\Omega_0h^2)(T/\text{MeV})^{-3}M_\odot $$ これより，宇宙初期の非常に早い時代には，宇宙論的に重要なスケールの摂動は地平線の外側にあったことが明らかである．ここに問題がある．もし宇宙の最初期に因果的な微視的過程が働き，原初密度ゆらぎを生じさせたと考えるなら，標準宇宙論における粒子地平線の存在は，関心のあるスケールで不均一性を生み出すことを事実上妨げてしまう[5]．有限の地平線サイズが再び障害となるのである．

• Spatial Flatness-Oldness

  FRWモデルにおいては，$\Omega_0$と$H_0$が現在の宇宙論モデルを特徴づける主要なパラメータであり[6]，$\Omega_0$と$H_0$から曲率半径$R_{\text{curv}} = H_0^{-2}/\sqrt{|\Omega_0-1|}$や密度$\rho_0 = (3H_0^2/8\pi G)\Omega_0$が決まる．現在の観測データは$\Omega_0$の値を[0.01, few]の範囲にしか制限していない．$\Omega_0$が1と大きく異ならないという事実は，$R_{\text{curv}} \sim H_0^{-1}$，$\rho_0 \sim \rho_{C}$であることを意味している．

  これは一見それほど驚くべきことではないように思えるかもしれないが，$\Omega$が時間とともに変化することを考慮すると，その意味は非常に驚くべきものである． \begin{align} \Omega(t) =& 1/[1-x(t)] \\ x(t) =& (k/R^2)(8\pi G\rho/3) \propto \begin{cases} &R(t)^2 & &(t \lesssim t_{\text{EQ}}) \\ &R(t) & &(t \gtrsim t_{\text{EQ}}) \end{cases} \end{align} $\Omega$が$1/(1-x)$として変化するため，過去に遡るほど$\Omega$は1に近づく．具体的には， \begin{align} |\Omega(10^{-43} \text{sec}) - 1| \lesssim& \mathcal{O}(10^{-60}) \\ |\Omega(1 \text{sec}) - 1| \lesssim& \mathcal{O}(10^{-16}) \end{align} さらに，これは宇宙の曲率半径がHubble半径と比べて非常に大きかったことも意味している： \begin{align} R_{\text{curv}}(10^{-43} \text{sec}) \gtrsim& 10^{30}H^{-1} \\ R_{\text{curv}}(1 \text{sec}) \gtrsim& 10^{8}H^{-1} \end{align}

  物理法則がこれを禁じているわけではないが，初期条件の観点から見ると，我々のFRWモデルは非常に特別なものであったことを示唆している．すなわち，Planck時代における初期条件は次のように特徴づけられる： \begin{align} |\Omega-1| \lesssim& \mathcal{O}(10^{-60}) \\ R_{\text{curv}} \gtrsim& 10^{30}H^{-1} \\ |(k/R^2)|/(8\pi G\rho/3) \lesssim& \mathcal{O}(10^{-60}) \end{align} もしこれらが成り立っていなければ，我々は今日とても困った状況にあっただろう．もし上記の量がPlanck時にすべてオーダー1であったなら，宇宙は$k>0$の場合「一瞬」（$\text{few}\times10^{-43}$ sec）で再崩壊してしまったか，$k < 0$ の場合は宇宙が$3$ Kに達するのがたった$10^{-11}$ secという「高齢」になってしまっただろう[7]．言い換えれば，宇宙論における自然な時間スケールはPlanck時間（$10^{-43}$ sec）であり，我々のFRWモデルは再崩壊も曲率支配にもならずに約$10^{60}$Planck時間を生き延びてきたのである．

• Unwanted Reliecs

  統一ゲージ理論の枠組みでは，初期宇宙で生成され，消滅を免れて現在のエネルギー密度に過剰に寄与するような，さまざまな安定かつ超重な粒子種が存在するはずである．磁気単極子（モノポール）はその最も顕著な例である．さらに，非常に大きな質量を持つ粒子種は，一般に消滅断面積が非常に小さい．熱的な残存粒子種の場合，$\Omega_X \propto \langle \sigma_A |v| \rangle^{-1}$ となるため，非常に重く安定な粒子種は「宇宙を支配したがる衝動（Hitler complex）」に悩まされる可能性が高い．

  標準宇宙論には，宇宙初期に過剰生成された遺物を取り除く仕組みが存在しない．

• Cosmological Constant

  Einstein方程式の最も一般的な形（一般共変性と両立するもの）は，悪名高い宇宙定数項を含んでいる： $$ R_{\mu\nu}-\frac{1}{2}g_{\mu\nu}\mathcal{R}=8\pi GT_{\mu\nu}+\Lambda g_{\mu\nu} $$ 宇宙定数項は，定数のエネルギー密度と等方的な圧力を持つ応力エネルギーの一種を追加することと等価であることが簡単に分かる： $$ \rho_{\text{VAC}}=\Lambda/8\pi G,\quad p_{\text{VAC}}=-\Lambda/8\pi G $$ 真空エネルギーの状態方程式は $w = p/\rho = -1$ である．$8\pi G$ の因子を除けば，宇宙定数項は真空に由来する応力エネルギーと同一である[8]．現代宇宙論では，真空エネルギーと宇宙定数という用語はほぼ同義で使われている．

  真空エネルギーによるFRW解（de Sitter解）は非常に興味深いものである． \begin{align} \rho_{\text{VAC}} =& \text{const} \\ H =& (8\pi G\rho_{\text{VAC}}/3)^{1/2} = \text{const} \\ R(t) \propto& \exp(Ht) \end{align} 膨張は減速するのではなく，時間とともに加速し，「共動体積内の全エネルギー」$E_{\text{TOT}} \propto R^3 p_{\text{VAC}}$は指数関数的に増加する． これらの事実は，もちろん真空エネルギーの「弾性的」な性質によるものである．真空の圧力はむしろ張力として記述されるべきであり，真空が行う$-pdV$仕事は，共動体積内のエネルギーを減らすのではなく増加させる． 膨張が減速せず加速することは，Newton的な観点からも理解できる．重力の有効な源である$\rho + 3p = -2\rho_{\text{VAC}}$が負になるためである．

  真空エネルギーのこのような特異な性質はインフレーション宇宙論にとって極めて重要であり，現在の膨張宇宙の状態とは一見矛盾しているように見える．観測に基づけば，真空エネルギー密度（$\rho_{\text{VAC}}$，あるいは$\Lambda/8\pi G$）は，せいぜい臨界密度と同程度であると考えてよいだろう．臨界密度は便利な単位系では $8.07 \times 10^{-47} h^2\,\text{GeV}^4$ である．この事実は，物理学のいかなる基本的なスケールと比べても現在の真空エネルギーが非常に小さいという，最後の謎につながる．

  上述の通り，宇宙項を禁じる既知の対称性は存在せず，一般的な観点からは $\Lambda/8\pi G \sim m_{\text{Pl}}^4$ が期待されるかもしれないが，これは現実とは122桁も異なっている！さらに，SSB（自発的対称性の破れ）に用いられるスカラー・ポテンシャルに関連するエネルギー密度は，相転移の際に $\sigma^4$ のオーダーで変化するが，場の量子論において現在の真空エネルギーがゼロ（あるいは $\sigma^4$ より十分小さい）ことを要求する既知の対称性原理は存在しない[9]．スカラー・ポテンシャルに関連するエネルギーの絶対値は，SSBや場の量子論の日常的な計算（例えば断面積など）には影響しない．しかし，真空エネルギーの重力的効果は非常に大きい．例えばクォーク/ハドロン転移に伴う比較的小さな真空エネルギー密度の変化 $\Delta V \sim \text{GeV}^4$ でさえ，今日の宇宙論的には許容できないほどである．

  現在の真空エネルギーが非常に小さい（あるいはゼロ）でなければならないことから，すべてのスカラーポテンシャルが $V(\sigma) = 0$（$\sigma$はポテンシャルの最小値）となるように調整するのが日常的な慣行となっている．この単純な操作は，真空エネルギーが初期宇宙で重要な役割を果たしうる可能性を示唆している．もしスカラー場がポテンシャルの最小値からずれていた場合，巨大な真空エネルギー（大統一スケールではおよそ $10^{56}\,\text{GeV}^4$）が存在することになる．後に見るように，このエネルギーこそがインフレーションを駆動する源である．インフレーションは他の宇宙論的な謎すべてに解決策を与えるが，宇宙定数問題そのものには光を当てていない．

  ここで挙げた問題はいずれも標準宇宙論そのものを否定するものではない．これらは標準宇宙論の枠組みの中で説明されてはいないが，矛盾するものでもない．宇宙論の目標は，物理法則に基づいて現在の宇宙の状態を説明することであり，いつか物理法則が上記の特徴をより明確に説明してくれることが期待される．インフレーションは，それを実現する有力な候補である．

  これらの問題点のうち最初の3つは，いずれも初期条件の問題に関わっている．これは人によっては宗教的な問題とも言えるだろう．いずれにせよ，我々のFRWモデルの初期条件は明らかに非常に特別なものである．この点はCollinsとHawkingによって具体的に示されており，我々の宇宙と質的に類似した進化を遂げる初期条件の集合は測度ゼロであることが示された．他の問題点は，いずれも何らかの形で標準宇宙論と現代の場の量子論の結びつきに関係している．この結合は，物質と反物質の宇宙論的非対称性に対する非常に魅力的な説明を与えるとともに，インフレーション宇宙論を生み出すことにもつながった．

  初期条件のジレンマは決して新しい問題ではなく，インフレーションが最初に提案された解決策というわけでもない．インフレーションの議論に進む前に，これまでのいくつかの試みについて簡単に触れておこう．Misnerらは「カオス的宇宙論」アプローチを提唱しており，より一般的で異方的かつ不均一な初期時空が，散逸的過程によって自らを平滑化し，我々の宇宙の巨大なエントロピーを生み出すことを期待していた．Penroseは，自然界では特定の種類の初期特異点しか許されない可能性を主張している．また，多くの研究者が，これらの問題の解決はPlanck時代に潜んでおり，（未知の）量子重力効果が答えを与えるのではないかと示唆してきた．後者2つのアプローチから派生した最近の考え方として，HartleとHawking，Vilenkinらによる「量子宇宙論」と宇宙の波動関数がある．ここで提案されているのは，古典的宇宙論の初期条件が，非常に初期の時代における時空の適切な量子的取り扱いの結果として生じる，というアイデアである．おそらく最も奇抜な「説明」は，人間原理への後退である．すなわち，もし宇宙や物理法則が現在のようでなければ，知的生命は発展せず，それらを発見し議論することもできなかっただろう，というものである[10]．

  これから明らかになるように，インフレーション理論の解決策は古典的な重力理論と，現代の場の量子論における十分に定式化された（とはいえ非常に推測的な）アイデアに基づいている．後で見るように，実現可能なすべてのインフレーションモデルでは，インフレーションはおよそ $10^{14}$ GeV 程度（$10^{-34}$ 秒程度）のエネルギースケールで起こる．もしインフレーションによる解決策が正しければ，インフレーション以前の歴史は（インフレーションの初期状態を与える可能性を除いて）本質的に意味を持たなくなる．

インフレーション：基本的な描像

インフレーションの基本的な考え方は，真空エネルギーが宇宙のエネルギー密度の主要な成分となっていた時代が存在し，その間スケール因子が指数関数的に成長した，というものである．このような時代（de Sitter位相として知られる）には，$H^{-1}$より小さい大きさの小さく滑らかで因果的に連結な領域が，今日の観測可能な宇宙全体を容易に包含するほどの共動体積にまで成長することができる．インフレーションの概念は，いまや自発的対称性の破れ（SSB）と結びつけられるよりもはるかに一般的なものと理解されているが，ここではまず対称性の破れを伴う相転移の文脈でインフレーションの基本を議論することから始める．それは，明確さや歴史的経緯のためだけでなく，もしそれが正しければインフレーションの魅力的な特徴となるからである．

対称性の破れを伴う相転移を考えよう．たとえば，GUT対称性の破れのように，エネルギースケールを $\sigma$（例：$\sigma\simeq10^{14}$ GeV）とする．温度が $\sigma$ より大きい場合，有限温度ポテンシャル $V_T(\phi)$ は $\langle \phi \rangle=0$ で最小となり，対称性は回復している．一次相転移では，臨界温度 $T_C$ に近づくと $\langle \phi \rangle=\sigma\neq0$ とは異なる位置に第2の極小値が現れる．臨界温度では2つの極小値がちょうど縮退し，$T_c$ より低い温度では対称性の破れた極小値がポテンシャルのグローバルな極小値となる．

どんな相転移でも，エネルギーだけが全てではない．$\langle\phi\rangle=0$ から $\langle\phi\rangle=\sigma$ への遷移は，エネルギー的に有利になった瞬間に即座に起こるわけではなく，その詳細や所要時間は理論のダイナミクスによって決まる．通常の実験室とは異なり，初期宇宙では状況が急速に変化している．たとえばGUTスケール（$10^{14}$ GeV）では，宇宙膨張の時間スケールはわずか $10^{-34}$ 秒程度であり，相転移に要する時間は宇宙の年齢と比べても無視できないほど大きくなりうる[11]．この事実は非常に興味深い物理をもたらす．

対称性が破れた基底状態への遷移の最初のステップは，$\langle \phi \rangle = 0$ と $\langle \phi \rangle = \sigma$ の間の障壁を越える過程である．これは，バリアを量子トンネルや熱的トンネルによってバブルが生成されることで進行する場合もあれば，臨界温度 $T_C$ より低い温度で障壁自体が消失する場合もある．我々の目的においては，その詳細は重要ではなく，宇宙のある領域でスカラー場 $\phi$ が空間的に一様で，障壁を越えているが，まだポテンシャルの最小値からは遠い状態にある，という事実だけが重要である[12]．

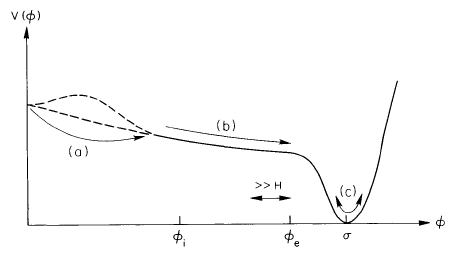
スカラー場$\phi$が（もし存在すれば）障壁を越えた後は，その真の真空への進化は古典的（しかも下り坂）である．次節で詳しく述べるが，$\phi$の古典的運動方程式は $$ \ddot{\phi}+3H\dot{\phi}+V'(\phi)=0 $$ で与えられる．これは摩擦（ここでは宇宙の膨張による）付きの坂を転がるボールの運動方程式と同じである．$\phi$の運動については次節で詳しく考察するが，ここで重要なのは$\phi$が最小値まで転がるのに要する時間である．スカラーポテンシャルが十分平坦であれば，この時間$\Delta t$は膨張の時間スケールよりも長くなりうる，すなわち$H\Delta t \gg 1$となる．その間，宇宙は巨大な真空エネルギー$\rho_{\text{VAC}} \simeq V(\phi=0) \equiv M^4$を持ち，宇宙の温度が$T \sim T_C \simeq M$より低くなると，この真空エネルギーが宇宙のエネルギー密度を支配するようになる．このとき，宇宙はde Sitter位相に入り，指数関数的に膨張し始める： $$ R(t)\propto\exp(Ht);\quad H^2=\frac{8\pi G}{3}V(\phi=0)\simeq M^4/m_{\text{Pl}}^2 $$

具体的に仮定すると，$\phi$が$0$から$\sigma$まで進化するのに要する時間が$\Delta t = 100H^{-1}$であるとしよう．de Sitter位相の指数関数的膨張の間，スケール因子は$\exp(100) \simeq 3 \times 10^{43}$という巨大な因子だけ増大する．標準的な値$M \simeq 10^{14}$ GeVを用いると，膨張の時間スケール$H^{-1}$は$10^{-34}$秒，ロールダウンに要する時間$\Delta t\simeq 10^{-32}$秒となる．ごく短い時間に多くのことが起こるわけである．$\phi$がゆっくりと最小値へ転がるこの期間は「スローロールオーバー」と呼ばれ，すべての実現可能なインフレーションモデルの重要な特徴である．$10^{-32}$秒というロールダウン時間は一見それほど遅くは感じられないかもしれないが，宇宙の膨張時間スケール（この例では$10^{-34}$秒）と比べれば，十分に「遅い」のである．

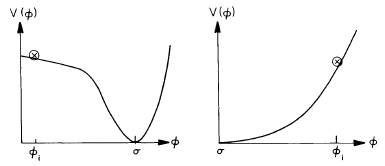
$\phi$がポテンシャルの最小値に近づくと，ポテンシャルは「急峻」になり，$\phi$の進化は加速する．$\phi$が最小値に近づき，必然的に最小値を通り過ぎると，$\phi=\sigma$のまわりでポテンシャルの曲率によって決まるHubble時間よりも短い時間スケールで振動し始める．このとき，スカラー場の巨大な真空エネルギーは，$\phi$場の空間的にコヒーレントな振動，すなわちゼロ運動量の$\phi$粒子の凝縮体の形で存在することになる．粒子生成，あるいは等価的には$\phi$粒子が結合している他のより軽い場へと崩壊することで，これらの振動は減衰する．そして，崩壊生成物が熱的平衡に達すると，宇宙は再加熱される．もし真空エネルギーの変換が完全に効率的であれば，再加熱温度$T_{\text{RH}}^4 \simeq V(\phi=0) \simeq M^4$となり，$T_{\text{RH}} \simeq M$となる．$\phi$が$\phi=0$から対称性の破れた極小値（$\phi=\sigma$）へ進化する様子は，上の図に示されている．

これが大まかな全体像である．より具体的に説明し，宇宙論的な問題がどのように解決されるかを示すため，次のパラメータを用いよう：$M = 10^{14}$ GeV，$H^{-1} = 10^{-34}$秒，$\Delta t = 100H^{-1} = 10^{-32}$秒，$T_c = T_{\text{RH}} = 10^{14}$ GeV．さらに，初期の滑らかな領域の大きさを$H^{-1} = 10^{-23}$ cmとするが，実際にはその初期サイズはほとんど重要でないことが後で分かる．インフレーションの本質的な特徴は，「再加熱」過程で生じる莫大なエントロピー生成である．インフレーション中の領域に含まれる初期エントロピーは$S_i \simeq T_C^3 (H^{-1})^3 \sim 10^{14}$であり，これは現在のHubble体積に含まれるエントロピーよりはるかに小さい．領域が指数関数的に膨張するにつれて，「超冷却」すなわち$T \propto \exp(-Ht)$が起こり，領域内のエントロピーは一定のままである．大きな出来事は再加熱であり，このとき温度は再び$10^{14}$ GeVまで上昇し，領域内のエントロピーは$S_f \simeq \exp(3H\Delta t) T_{\text{RH}}^3 (H^{-1})^3 \simeq 10^{44}$まで増加する．領域の最終的な大きさは$\exp(H\Delta t) H^{-1} \simeq 3 \times 10^{20}$ cmとなる．非常に非断熱的な再加熱過程によって，インフレーション領域内のエントロピーは$10^{130}$倍に増加する．これはブラジル基準でも「インフレ的」に大きい！再加熱の非断熱性は下図に示されている．

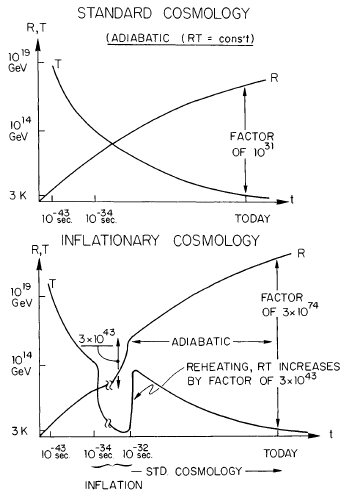
この莫大なエントロピーの増加によって，4つの宇宙論的問題のうち3つが一挙に解決される．まず，大域的な滑らかさの問題が解決される．インフレーション前には現在観測される宇宙のエントロピーのごく一部しか含まれていなかった滑らかな領域が，インフレーション後には観測可能な宇宙のエントロピーをはるかに上回るエントロピーを持つようになる．今日私たちが観測できる全てを含む共動体積は，インフレーション後の滑らかな領域の中に容易に収まる（その$10^{56}$倍もの大きさがある）．別の見方をすると，インフレーション後は $R \times T^{-1}$ が成り立つので，現在のハッブル体積は宇宙の温度が $10^{14}$ GeV だったとき，わずか約30 cmの大きさしかなかったことになる．これはインフレーション後の滑らかな領域のサイズ（$\simeq 3 \times 10^{20}$ cm）よりもはるかに小さい．

次に，空間の平坦性・古さの問題も解決される．インフレーションの間，宇宙のエネルギー密度は一定のまま，曲率半径は指数関数的に増大する．その結果，$x = (k/R^2)/(8\pi G\rho/3)$ の比は約 $\exp(200)$ だけ減少する．したがって，現在の宇宙の曲率半径は，現在のHubble半径よりもはるかに大きいままであり，これによって宇宙の平坦性が「説明」され，$\Omega_0$ が1に指数関数的に近いことが「予言」される．

最後に，エントロピーの増加は不要な残存粒子種の問題も解決する．インフレーション以前に生成された不要な残存粒子種があったとしても，その存在度$(n_X/s)_i$は，インフレーション後にはエントロピーの増加と同じ指数関数的な因子だけ減少し，$(n_X/s)_f = \exp(-300)(n_X/s)_i$ となる．さらに，宇宙の初期エントロピーは本質的に無関係であり，今日観測される熱は130桁にわたってほぼすべて再加熱時に生成されたものである．言うまでもなく，宇宙のバリオン非対称性はインフレーション後に生成されなければならないが，再加熱温度が十分高ければ通常通り生成されうる．

ここまで述べてきたように，インフレーションは小スケールの不均一性の問題を解決しない．インフレーション後の領域は完全に滑らかであり，古典的には一様なスカラー場から再加熱後に一様な放射温度が生じる．しかし，密度ゆらぎはスカラー場の量子的揺らぎによって生じる．また，インフレーションは宇宙定数問題にも何ら光を当てていない．

ここで述べたインフレーションのバージョンは，Guthが1981年に提案した元々のモデルではなく，1982年にLinde，およびAlbrechtとSteinhardtによって提案された変種であり，「新しいインフレーション」あるいはより適切には「スローロールオーバー・インフレーション」と呼ばれるものである．この名称が示す通り，スカラー場がポテンシャルの最小値へゆっくりと進化することが鍵となる特徴である．今日のほとんどすべてのインフレーションモデルはこの単純な原理に基づいている．

Guthによる最初の（そして成功しなかった）インフレーションモデルは，現在「オールド・インフレーション」と呼ばれており，現在のインフレーション像とは決定的に異なる点があった．オールド・インフレーションでは，スカラー場が$\langle \phi \rangle=0$の偽の真空状態に閉じ込められている間に指数関数的な膨張が起こり，$\phi$がゆっくりと（しかし必然的に）$\phi=\sigma$へ転がり落ちる間ではなかった．そのため，十分なインフレーションを実現するにはトンネル遷移率が小さいこと，すなわち真の真空バブルの生成が稀であることが必要だった．一方，再加熱に必要な潜熱（偽の真空エネルギー）はバブル壁の運動エネルギーとして蓄えられ，再加熱はバブル同士の衝突によって進行しなければならなかった．結局，十分なインフレーションに必要なトンネル遷移率の小ささが，バブル衝突による再加熱を妨げ，宇宙の相転移は完了せず，ほとんどの宇宙は永遠にインフレーションを続けることになってしまった．

スカラー場のダイナミクスとしてのインフレーション

現在理解されているインフレーションの最も一般的な定式化は，弱く結合したスカラー場がそのポテンシャルの最小値からずれていた状態から動的に進化する現象である，というものである．したがって，インフレーションの力学を理解する鍵は，膨張宇宙におけるスカラー場のダイナミクスにある．

スカラー場の進化を解析可能にするためには，いくつかの単純化した仮定を置く必要がある．これらの仮定はいずれも非常に妥当であり，後ほど示すように十分に正当化されるものである．具体的には次の通りである．

• 膨張率が次式で与えられる背景RW時空を仮定する： $$ H^2 = \frac{8\pi G}{3} \rho_{\phi} - \frac{k}{R^2} $$ ここで$\rho_{\phi}$はスカラー場に由来するエネルギー密度である．RW時空を仮定するのは一見トートロジーのように思えるかもしれないが，解析を容易にするだけでなく，後の節で見るように，インフレーションが始まって間もなく時空は急速にRWモデルへと近づくため，十分に正当化される．その他のエネルギー成分は急速に赤方偏移して無視できるため，これも良い近似である．
• スカラー場は（少なくとも$H^{-1}$に比較できるスケールで）空間的に一様であり，初期値$\phi_i$はポテンシャルのグローバルなゼロエネルギー極小値$\sigma$からずれていると仮定する（すなわち$V(\sigma) = V'(\sigma) = 0$）．不均一性が十分小さい場合（この条件は後で定量的に述べる），空間勾配は急速に赤方偏移して無視できるため，$\phi$のゼロ運動量モードのみが重要となる．
• スカラー場の量子的揺らぎは，場の古典的運動に対する小さな補正として扱う．すなわち， $$ \phi(t)=\phi_{\text{cl}}+\delta\phi_{\text{QM}}; \quad \Delta \phi_{\text{QM}} \ll \phi_{\text{cl}} $$ 次節で量子的揺らぎの重要な役割について議論し，この仮定が正当化されることも示す．簡単のため，以降は「cl」の添字は省略する．

  最小結合されたスカラー場$\phi$を考え，そのラグランジアン密度は $$ \mathcal{L}=\partial^{\mu}\phi\partial_{\mu}\phi/2-V(\phi)=\dot{\phi}^2/2-V(\phi) $$ で与えられる[13]．ここでは$\phi$が他の場と持つ相互作用は無視する．実際，インフレーションが成功するためにはそれらの相互作用は非常に弱くなければならないので，この仮定は自己無撞着である．$\phi$場のストレスエネルギーは $$ T^{\mu\nu}=\partial^{\mu}\phi\partial^{\nu}\phi-\mathcal{L}g^{\mu\nu} $$ $\phi$が空間的に一様であると仮定すると，$T^{\mu\nu}$は完全流体の形となり，エネルギー密度と圧力は \begin{align} \rho_{\phi} =& \dot{\phi}^2/2+V(\phi) & &[+(\nabla\phi)^2/2R^2] \\ p_{\phi} =& \dot{\phi}^2/2-V(\phi) & &[-(\nabla\phi)^2/6R^2] \end{align} で与えられる．

  参考までに，かっこ内に空間勾配項も示した（$\nabla$は共動座標でのもの）．ストレスエネルギーへの空間勾配の寄与は$\exp(-2Ht)$で減衰するため，すぐに無視できるようになる．また，もし空間勾配が支配的ならば，スカラー場は$p=-\rho/3$の流体のように振る舞い，$R(t)\propto t$となりインフレーションは起こらないことも分かる．

  $\phi$の古典的運動方程式は，作用$S_\phi=\int d^4x \sqrt{-g}\mathcal{L}$の変分，またはエネルギー運動量保存則（$T^{\mu\nu}_{;\nu}=0$）から導かれる．いずれにせよ， $$ \ddot{\phi}+3H\dot{\phi}+\Gamma_{\phi}\dot{\phi}+V'(\phi)=0 $$ となる．$3H\dot{\phi}$項は宇宙膨張によるもので，場の運動量の赤方偏移に対応する．$\Gamma_\phi\dot{\phi}$項はラグランジアン密度からは直接出てこないが，これは$\phi$場が他の場と結合している場合，量子的粒子生成による減衰を表す．$\phi$場の空間的にコヒーレントな振動は質量$m^2_{\phi}=V''(\sigma)$のゼロ運動量の$\phi$粒子の凝縮体に対応し，これが他の軽い粒子種へ崩壊することで宇宙の再加熱が起こる．この減衰幅$\Gamma_\phi$は$\phi$粒子の崩壊幅そのものである．例えば，$\phi$粒子が2つの軽いフェルミオンに崩壊し，結合定数$h$で結合している場合，崩壊幅は$\Gamma_\phi = h^2 m_\phi / 8\pi$となる．

  この運動方程式は，摩擦付きで谷に向かって坂を転がるボールの運動と同じであり，2つの質的に異なる領域がある．それぞれ解析的に解ける[14]．1つは「スローロール」領域で，摩擦が支配的で$\phi$は「終端速度」でゆっくり転がる．もう1つは急速振動領域で，$\phi$は減衰した単振動子のように振る舞う．以下，それぞれについて述べる．

• スローロール： この領域では，$\ddot{\phi}$項は無視でき，粒子生成項も働かない[15]．スローロール中，運動方程式は $$ 3H\dot{\phi} = -V'(\phi) $$ となる．すなわち，膨張による摩擦がポテンシャルの傾きによる加速と釣り合っている．$\ddot{\phi}$を無視できるための整合条件は \begin{align} |V''(\phi)| &\ll 9H^2 \simeq 24\pi V(\phi)/m_{\text{Pl}}^2 \\ |V'(\phi)m_{\text{Pl}}/V(\phi)| &\ll (48\pi)^{1/2} \end{align} である．これら2つの条件がスローロールの持続時間を決め，またスカラー場の運動エネルギー（$\dot{\phi}^2/2$）がポテンシャルエネルギーより十分小さいことも保証する．したがって $$ H^2 \simeq \frac{8\pi}{3m_{\text{Pl}}^2}V(\phi) $$ となる．

  上式を用いると，$\phi$が$\phi_1$から$\phi_2$まで転がる間にスケール因子が増加する$e$-fold数は簡単に計算できる： $$ \ln(R_2/R_1) \equiv N(\phi_1\to\phi_2)\equiv\int_{t_1}^{t_2}Hdt=-\frac{8\pi}{m_{\text{Pl}}^2}\int_{\phi_1}^{\phi_2}\frac{V(\phi)}{V'(\phi)}d\phi $$ ここで，$dt = d\phi/\dot{\phi}$を用いた．

  多項式型ポテンシャルでは，$V''(\phi) \sim V'(\phi)/\phi$となり，$N(\phi_1\to\phi_2) \sim 3H^2/V''$となる．これは最初のスローロール条件から$N \gg \mathcal{O}(1)$となる．すなわち，スローロール条件を満たすほど平坦なポテンシャルであれば，$\phi$が転がる間にスケール因子は多くの$e$-foldだけ増大する．インフレーションの総$e$-fold数は$N_{\text{TOT}} \equiv N(\phi_i \to \phi_e)$で与えられ，$\phi_e$はスローロール条件が破れる点（通常は$\phi_e \simeq \sigma$）で決まる．

• コヒーレント振動：この領域では $V'' \gg H^2$ となり，$\phi$ は膨張時間スケールで急速に進化する．さらに，$\phi$ がポテンシャルの底に到達すると，$\omega^2=V''(\sigma)$ で決まる周波数で振動し始めます．急速振動領域では， $$ \dot{\rho}_{\phi}+3H\dot{\phi}^2+\Gamma_{\phi}\dot{\phi}^2=0 $$ のように，$\dot{\phi}$を掛けて書き直すと便利である．$\phi$は$\sigma$の周りで急速に振動するので，$\dot{\phi}^2$は正弦的に振動し，その振動周期で平均化できる[16]： $$ \langle \dot{\phi}^2 \rangle_{\text{cycle}} = \rho_{\phi} $$ この置き換えを用いると，$\rho_\phi$の進化方程式は $$ \dot{\rho}_{\phi}+3H\rho_{\phi}+\Gamma_{\phi}\rho_{\phi}=0 $$ となる．重い粒子種の減衰を記述する方程式と同じである．この方程式の解は以下の式で与えられる： $$ \rho_{\phi}=M^4(R/R_{\text{osc}})^{-3}\exp[-\Gamma_{\phi}(t-t_{\text{osc}})] $$ ここで "osc" はコヒーレント振動が始まる時点を表し，$M^4$はその時のスカラー場の真空エネルギーである．

  再加熱過程の議論をできるだけ一般的に保つため，$\phi$粒子の崩壊生成物が$\phi$自身に比べて十分軽く，したがって高い相対論的であると仮定する．すると再加熱を記述する追加の方程式は \begin{align} \dot{\rho}_R+4H\rho_R =& \Gamma_{\phi}\rho_{\phi} \\ H^2 =& 8\pi G(\rho_{\phi}+\rho_R)/3 \end{align} となる．$\rho_R$は崩壊生成物のエネルギー密度である．$\rho_R$の運動方程式はエネルギー保存則から導かれる．生成物が十分相互作用して熱平衡に達すると，$\rho_R = g_* \pi^2 T^4 /30$ となる．

  再加熱過程を記述する方程式は，非平衡下での重い非相対論的粒子種の崩壊を記述するものと同一である．ここでその特徴を簡単に復習する．

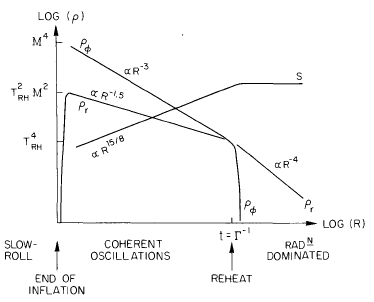
  $t = t_{\text{osc}}\simeq H^{-1}\sim m_{\text{Pl}}/M^2$から $t \sim \Gamma_\phi^{-1}$ まで，非相対論的な$\phi$粒子（コヒーレント振動）が質量密度を支配し，宇宙は物質優勢となる：$R(t) \propto t^{2/3}$．de Sitter位相で極端な超冷却が起こっているため，振動開始時点では$\rho_R = 0$である．この$\phi$優勢期における$\rho_R$の近似解は \begin{align} \rho_R \simeq& \frac{m_{\text{Pl}}^2\Gamma_{\phi}}{10\pi t}[1-(t/t_{\text{osc}})^{-5/3}] \\ \simeq& \frac{(6/\pi)^{1/2}}{10}m_{\text{Pl}}\Gamma_{\phi}M^2(R/R_{\text{osc}})^{-3/2}[1-(R/R_{\text{osc}})^{-5/2}] \end{align} となる．すなわち，$\rho_R$は0から$m_{\text{Pl}}^{1/2}\Gamma_{\phi}M^2$程度まで急速に増加し，その後$R^{-3/2}$で減少する．再加熱中の温度は実際には減少する．したがって，再加熱中に達する最大温度は $$ T_{\text{max}} \simeq 0.8g_*^{-1/4}M^{1/2}(\Gamma_{\phi}m_{\text{Pl}})^{1/4} $$ となる．この期間，共動体積あたりのエントロピー$S \propto R^3 \rho_R^{3/4}$は$R^{15/8}$として増加する．

  $t \simeq \Gamma_\phi^{-1}$になると$\phi$粒子が急速に崩壊し，宇宙は放射優勢となり，共動体積あたりのエントロピーは一定になる．これは標準宇宙論の通常の断熱的放射優勢期の始まりである．このときの温度（再加熱温度）は $$ T_{\text{RH}} \equiv T(t=\Gamma_{\phi}^{-1})\simeq0.55g_*^{-1/4}(m_{\text{Pl}}\Gamma_{\phi})^{1/2} $$ である．$\phi$優勢期の結果，再加熱温度は$\Gamma_\phi$で決まり，初期真空エネルギー$M$ではなく，一般に$T_{\text{RH}} < M$となる．コヒーレント振動期に初期真空エネルギーの多くは赤方偏移で失われ，$M^4/T_{\text{RH}}^4$だけ減少する[17]．

  $T_{\text{max}} \equiv T(t=t_{\text{osc}}) \simeq (T_{\text{RH}} M)^{1/2}$が再加熱過程で達する最大温度だが，実用上は$T_{\text{RH}}$が「再加熱温度」とみなされる．なぜなら，コヒーレント振動期にはエントロピーが増加し，生成されうる残存粒子種（モノポール，バリオン数，アクシオンなど）の存在度もその後のエントロピー放出で希釈されるからである．下図に再加熱過程の概要を示す．

  再加熱直後，あるいは再加熱中に，重要なイベントが起こる必要がある：バリオン生成である．インフレーション前のバリオン非対称性は指数関数的に希釈されてしまうからである．バリオン生成には少なくとも2つの方法がある：(1)通常の$X$ボソンの非平衡崩壊，(2)$\phi$粒子自身の崩壊による直接生成．前者は$X$ボソンはまず熱浴から生成される必要があり，そのためには$T_{\text{RH}}$が$X$ボソン質量以上でなければならない．後者は極端な非平衡崩壊で，この場合バリオン非対称性は$n_B/s \simeq eT_{\text{RH}}/m_\phi$となる．

  再加熱過程の知識をもとに，平滑性・平坦性問題を解決するのに必要なインフレーション量（指数関数的成長の$e$-fold数）を計算できる．平滑性問題を解決するには，インフレーション終了時の領域に$10^{88}$以上のエントロピーが必要である．初期領域の大きさをインフレーション開始時のHubble半径$H^{-1} \sim m_{\text{Pl}}/M^2$とすると，インフレーション中に$\exp(N_{\text{TOT}})$倍，再加熱中に$R_{\text{RH}}/R_{\text{osc}}\simeq (M^4/T_{\text{RH}}^4)^{1/3}$倍成長します．したがって最終的なエントロピーは $$ S_{\text{patch}}\simeq \exp(3N_{\text{TOT}})(M^4/T_{\text{RH}}^4)H^{-3}T_{\text{RH}}^3 \simeq \exp(3N_{\text{TOT}})\frac{m_{\text{Pl}}^3}{M^2T_{\text{RH}}} $$ となる．$S_{\text{patch}} > 10^{88}$を要求すると $$ N_{\text{TOT}}\gtrsim N_{\text{min}}=53+\frac{2}{3}\ln(M/10^{14}\,\text{GeV})+\frac{1}{3}\ln(T_{\text{RH}}/10^{10}\,\text{GeV}) $$ となる．$M$と$T_{\text{RH}}$を$1$ GeVから$10^{19}$ GeVまで変化させても$N_{\text{min}}$は24から68の範囲しか変化しない．また，再加熱温度が下がるほど必要なインフレーション量は（対数的に）減少する．$\phi$優勢期が長いほど再加熱温度は下がるが，生成されるエントロピーは増加する．

  次に平坦性問題である．インフレーション前の曲率半径は$H$とインフレーション前の$\Omega$で $$ (R_{\text{curv}})_i = \frac{H^{-1}}{|\Omega_i-1|^{1/2}} $$ で与えられる．インフレーション中に$\exp(N_{\text{TOT}})$倍，$\phi$優勢期に$(M^4/T_{\text{RH}}^4)^{1/3}$倍成長します．これを用いて曲率半径内のエントロピーは $$ S_{\text{curv}}\equiv(R_{\text{curv}})_{\text{RH}}^3T_{\text{RH}}^3\simeq\frac{\exp(3N_{\text{TOT}})m_{\text{Pl}}^3/(M^2T_{\text{RH}})}{|\Omega_i-1|^{3/2}} $$ となり，$\Omega_i$以外はインフレーション後の領域のエントロピーと同じです．曲率体積内のエントロピーは（膨張が断熱的なら）一定なので，平坦性問題を解決するには$S_{\text{curv}}$が現在のHubble体積内のエントロピーより大きくなるだけのインフレーションが必要である．すなわち $$ N'_{\text{min}}=53+\frac{2}{3}\ln(M/10^{14}\,\text{GeV})+\frac{1}{3}\ln(T_{\text{RH}}/10^{10}\,\text{GeV})+\frac{1}{2}\ln(|\Omega_i-1|) $$ となり，$\Omega_i$の項以外は平滑性問題と同じである．さらに，現在の曲率半径とHubble半径の比は $$ R_{\text{curv}}/H_0^{-1}=\frac{\exp(N_{\text{TOT}}-N_{\text{min}})}{|\Omega_i-1|^{1/2}} $$ で与えられ，現在の$\Omega$は $$ |\Omega_0-1|=\exp[2(N_{\text{min}}-N_{\text{TOT}})]|\Omega_i-1| $$ となる．インフレーションが十分長ければ$N_{\text{TOT}} \gg N_{\text{min}}$となり，$S_{\text{patch}} \gg 10^{88}$，$|\Omega_0-1| \ll 1$が実現される．

密度揺らぎと残存重力子

古典的なレベルでは，インフレーション領域内で$\phi$が一定であることにより，インフレーション後のパッチ内の温度が一様であることが保証される．再加熱はインフレーション領域内の$\phi$の値によって完全に制御される．しかし，インフレーションは運動学的にも力学的にも，宇宙論的に重要なスケールで密度揺らぎを生成する手段を持っている．密度揺らぎの生成の力学には，de Sitter空間におけるスカラー場に必然的に生じる量子力学的揺らぎが関与する．

まず，インフレーションが密度揺らぎの生成を可能にする運動学的側面について説明しよう．標準宇宙論では，すべての共動スケール$\lambda$は地平線を一度だけ横切る[18]．すなわち，最初は地平線より大きく（$\lambda_{\text{phys}} \gg H^{-1}$），その後ある時点で地平線内に入る．放射優勢期に地平線内に入る共動スケール（$\lambda \lesssim 13(\Omega_0 h^2)^{-1}$ Mpc）の場合，地平線進入時の宇宙の温度は $$ T_{\text{HOR}}(\lambda) \simeq 63\,\text{eV}\,g_*^{-1/2}g_{*S}^{1/3}(\lambda/\text{Mpc})^{-1} $$ 一方，宇宙が物質優勢のときに地平線内に入るスケール（$\lambda \gtrsim 13(\Omega_0 h^2)^{-1}$ Mpc）の場合，温度は $$ T_{\text{HOR}}=950\,\text{eV}(\Omega_0 h^2)^{-1}(\lambda/\text{Mpc})^{-2} $$

インフレーション中はHubbleパラメータが一定であるため，宇宙論的に重要なすべてのスケールは最初は地平線（Hubble半径）より小さいサイズから始まり，インフレーションの間に地平線の外側へと出ていき，その後（通常の時代に）再び地平線内に戻ってくる．この「さよなら」と「再会」の特徴こそが，インフレーションが宇宙論的に重要なスケールに密度揺らぎを刻み込むことを運動学的に可能にしている．これは図に示されている．大まかに言えば，あるスケールでの量子揺らぎは，そのスケールが地平線より小さいときに発生し，地平線の外側に出るとこれらの揺らぎは「凍結」して古典的な時空の摂動となり，最終的に地平線内に再突入したときに密度揺らぎとして現れる．

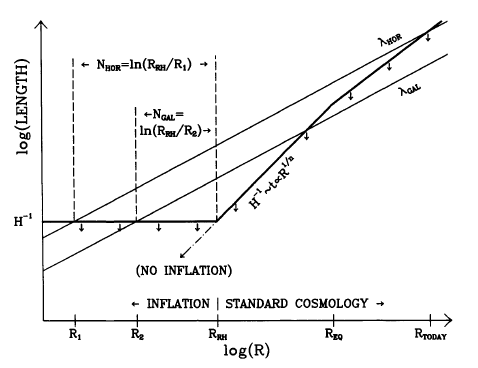
摂動のスペクトルを解析するためには，インフレーション期において特定のスケールが地平線の外に出るタイミングを知る必要がある．図から明らかなように，インフレーション宇宙論では「最初に出たものが最後に戻る（first out—last in）」となる．あるスケールが地平線を出てからインフレーションが終わるまでの$e$-fold数で指定するのが便利である．前節の最後で計算したように，現在のハッブル半径（約$3000\,\text{Mpc}/\lambda$）に対応するスケールが地平線を出たのは $$ N_{3000\,\text{Mpc}}=N_{\text{min}}=53+\frac{2}{3}\ln(M/10^{14}\,\text{GeV})+\frac{1}{3}\ln(T_{\text{RH}}/10^{10}\,\text{GeV}) $$ である（図参照）．

インフレーションに関して重要なポテンシャルは，その領域で非常に平坦であるため（$|V''| \ll H^2$），インフレーションのスローロール期間中はスカラー場$\phi$を質量ゼロとして扱うのが非常に良い近似となる．de Sitter空間における最小結合された質量ゼロスカラー場は，次のような量子揺らぎのスペクトルを持つ： $$ (\Delta\phi)_k^2 \equiv V^{-1}k^3|\delta\phi_k|^2/2\pi^2 = (H/2\pi)^2 $$ ここで，スカラー場の揺らぎはFourier成分に分解されている： $$ \delta\phi_k = \int d^3x\, \exp(i\vec{k}\cdot\vec{x})\phi(\vec{x}) $$ 各スケール$k$での揺らぎのパワー$(\Delta\phi)_k$は，de Sitter空間の事象の地平線に対応するGibbons-Hawking温度$T_{\text{GH}} = H/2\pi$によって与えられることに注意．$\phi$の平均二乗揺らぎは次式で与えられる： $$ (\Delta\phi)^2 = \frac{V^{-1}}{2\pi^2}\int k^2 dk\, |\delta\phi_k|^2 = N(t)(H/2\pi)^2 $$ ここで$N(t) \simeq Ht$はインフレーション開始からの$e$-fold数である[19]．予想される通り，$\phi$の量子揺らぎの大きさは$H/2\pi$で決まる．

因果的な微視的物理過程は，Hubble半径より小さい距離スケールでのみ作用する．なぜなら，Hubble半径は膨張時間内に光信号が到達できる距離を表すからである．各モード $k$ が地平線の外側へ出ると，微視的物理から切り離され，「凍結」して古典的な揺らぎとして残る[20]．各モード $k$ の古典的な進化は次の式で記述される： $$ \delta\ddot{\phi}_k+3H\delta\dot{\phi}_k+\frac{k^2}{R^2}\delta\phi_k=0 $$ 地平線より大きい（$k \ll RH$）モードについては，この方程式の解は非常に単純で，$\delta\phi_k = \text{const.}$ となる．

より重要なのは，スカラー場 $\phi$ の揺らぎによって生じるエネルギー密度摂動である．ポテンシャルエネルギー密度はスカラー場 $\phi$ に依存するため，$\phi$ の揺らぎはエネルギー密度の摂動を引き起こす： $$ \delta \rho_\phi = \delta \phi(\partial V/\partial \phi) $$ 後の章で古典的なスカラー型の計量（または密度）摂動の進化について詳しく議論している．特に，地平線の外側にあるモードの密度摂動の進化は微妙であり，一般相対論のゲージ自由度のために物理的なモードとゲージアーティファクトを区別するのが難しい[21]．微視的な物理過程はHubble半径より大きいスケールでは作用できないため，密度摂動の進化は基本的に運動学的で非常に単純であると予想される．実際，その通りである．

ゲージ不変量 $\zeta$ の進化は，Hubble半径より大きい摂動（スーパーHubbleスケール）では特に単純で，$\zeta = \text{const}$ となる．地平線進入時（$\lambda\simeq H^{-1}$）には $\zeta = \delta\rho/(\rho+p)$ という特に単純な形になる．通常の物質優勢期（MD）や放射優勢期（RD）では，地平線進入時の $\zeta$ はオーダー1の係数を除けば $\delta\rho/\rho$ に等しい．したがって，密度摂動が再び地平線内に入るときの振幅 $(\delta\rho/\rho)_{\text{HOR}}$ を計算するには，インフレーション中にその摂動が地平線の外側に出た時点での $\zeta$ を求めればよい．インフレーション中は $\rho_{\phi} + p_{\phi} = \dot{\phi}^2$ は $\rho_\phi\simeq V(\phi)$ に比べて非常に小さいので，$\zeta$ は $\delta\rho/\rho$ よりもはるかに大きくなる．2回の地平線横断時の $\zeta$ の値を等しいとすると，次式が得られる： $$ \begin{pmatrix} 3/4 & (\text{RD}) \\ 1 & (\text{MD}) \end{pmatrix} \left(\frac{\delta\rho}{\rho}\right)_{\text{HOR}} = \zeta_{N_\lambda} = \left( \frac{\delta\phi\, V'}{\dot{\phi}^2} \right)_{N_\lambda} \simeq \left( \frac{H^2}{\dot{\phi}} \right)_{N_\lambda} $$ ここで，$\delta\phi\simeq H/2\pi$ の揺らぎとスローロール方程式 $V' = -3H\dot{\phi}$ を用いた．

インフレーション中，$H$や$\dot{\phi}$は非常にゆっくりとしか変化しない．また，宇宙論的に重要なスケール，例えば1 Mpcから3000 Mpcに対応するモードは，インフレーション全体（およそ60 $e$-folds）のうちごく一部，約8 $e$-foldsの間に地平線の外側へ出ている[22]．その結果，予言される揺らぎのスペクトルはほぼスケール不変，すなわちHarrison-Zel'dovichスペクトルとなる[23]．これはインフレーションの非常に堅牢かつ一般的な予言であり，de Sitter空間の時間並進対称性に由来する．各モードが地平線の外側へ出るとき，物理的なサイズ（$\sim H^{-1}$）も宇宙の膨張率も同じなので，すべてのスケールに同じ振幅の「しわ」が刻み込まれることになる．さらに，量子的揺らぎの性質から，スカラー場の自己結合が十分小さければ，誘起される密度揺らぎはGauss型となる[24]．

一方，曲率ゆらぎが一定となるスペクトルの振幅はモデル依存であり，$H^2/\dot{\phi}$に依存する．観測される宇宙構造の種となるためには，$10^{-5}$から$10^{-4}$程度の摂動振幅が必要と考えられる．CMBRの等方性観測から，振幅は$10^{-4}$を超えてはならないことが分かっている．次節で見るように，この条件を満たすモデルを見つけるのは決して容易ではない．許容される密度ゆらぎを実現することは，インフレーションポテンシャル（ひいては素粒子物理モデル）に対する最も厳しい制約となり，インフレーションポテンシャルが極めて平坦でなければならないことを要求する．

先に進む前に，密度揺らぎの振幅について非常に正確に述べておこう．rms質量ゆらぎは，$\phi$ の rms 分散と次のように関係している： $$ (1\,\text{or}\,3/4)[k^{3/2}|\delta_k|/\sqrt{2}\pi]=(\Delta\zeta)_{N_\lambda}\simeq[k^{3/2}|\delta\phi_k|/\sqrt{2}\pi](V'/\dot{\phi}^2) $$ 宇宙がまだ放射優勢の間に地平線へ再突入するモード $k$，すなわち $\lambda \lesssim 13h^{-2}$ Mpc の場合，これらは光子・バリオンプラズマ中の音波として再突入し，その振幅は $$ (\delta\rho/\rho)_{\text{HOR}}(\equiv k^{3/2}|\delta_k|/\sqrt{2}\pi)=\left( \frac{2H^2}{\pi\dot{\phi}} \right)_{N_\lambda} $$ 相互作用しない残存粒子（アクシオン，フォティーノなど）の摂動も，等価原理により同じ振幅を持つ必要があるが，もちろん振動はしない．その代わり，物質・放射等価の時点までに2から3倍の対数的成長をする．

宇宙が物質優勢のときに地平線へ再突入するモード $k$（すなわち $\lambda \gtrsim 13h^{-2}$ Mpc）は，成長モードの摂動として再突入し，その振幅は $$ (\delta\rho/\rho)_{\text{HOR}}\simeq\left( \frac{H^2}{5\pi\dot{\phi}} \right)_{N_\lambda} $$ となる．次章で詳しく述べるが，物質・放射等価期における密度揺らぎのスペクトルが，構造形成問題の「初期条件」となる．次章では，これらの地平線横断時の振幅を，物質・放射等価期で指定される振幅へと「翻訳」する．

全ての質量ゼロ，あるいは非常に軽い（$m^2 \ll H^2$）場は，de Sitter空間において同様の方法で励起され，そのスペクトルは上式で与えられる．励起されたモードが地平線内に再突入すると，それらは粒子として伝播する．すなわち，de Sitter空間での励起は最終的に粒子生成をもたらす．非常に興味深い例として，重力子場を考えよう．重力子は，横波かつトレースレスなテンソル型計量摂動に対応する伝播モードであり，2つの自由度を持つ最小結合スカラー場として振る舞う．したがって，重力子の生成は2つの最小結合スカラー場$\phi_{+,\times}$を考えることで解析でき，これは次のように無次元のテンソル型計量摂動$h^i{}_j$と関係している： \begin{align} h_{+,\times} =& \sqrt{16\pi G}\phi_{+,\times} \\ h^{i}{}_{j} =& h_{+}\bm{e}_{+} + h_{\times}\bm{e}_{\times} \end{align} ここで，$\bm{e}_{+} = \bm{e}_x \otimes \bm{e}_x - \bm{e}_y \otimes \bm{e}_y$，$\bm{e}_{\times} = \bm{e}_x \otimes \bm{e}_y + \bm{e}_y \otimes \bm{e}_x$は，2つの重力子モードの偏光テンソルである．

$h_{+,\times}$における平均揺らぎは，最小結合スカラー場の場合の先ほどの公式に $\sqrt{16\pi G}$ を掛けることで得られ，次式で与えられる： $$ (\Delta h_{+,\times})_k \equiv k^{3/2}|h_k|/\sqrt{2}\pi=\frac{2}{\sqrt{\pi}}\frac{H}{m_{\text{Pl}}} $$ 質量ゼロ・最小結合スカラー場の場合と同様に，あるモード $k$ の振幅は，そのモードが地平線の外側にある間は一定のままである． ある重力子モードが地平線内に再突入すると，それに対応するテンソル型計量揺らぎは以後重力子として伝播する． あるモードが地平線内に再突入する際の重力子のエネルギー密度は，簡単に見積もることができる[25]： \begin{align} k\frac{d\rho_{\text{graviton}}}{dk} =& \frac{k^2[(\Delta h_+)_k^2+(\Delta h_{\times})_k^2]}{16\pi G} \\ \simeq& \frac{k_{\text{phys}}^2}{2\pi^2G}\left( \frac{H}{m_{\text{Pl}}} \right)^2\simeq \frac{H_{\text{HOR}}^2H^2}{2\pi^2} \\ \frac{k}{\rho_{\text{HOR}}}\frac{d\rho_{\text{graviton}}}{dk} \simeq& \frac{4}{3\pi}\left(\frac{H}{m_{\text{Pl}}}\right)^2 \end{align} ここで "HOR" の添字は，インフレーション後の宇宙で地平線進入時の時代を表す． この計算を丁寧に行うことで，インフレーションによって生成され，今日存在するはずの重力波背景のスペクトルを求めることができる． その結果の一例が図に示されている．

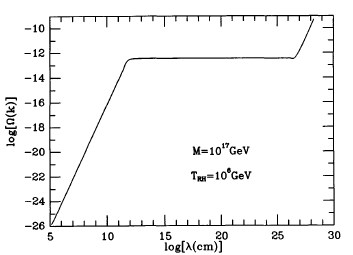
上式から，地平線進入時の重力子の1オクターブあたりのエネルギー密度（$k\,d\rho_{\text{graviton}}/dk$）は，宇宙全体のエネルギー密度の約$(H/m_{\text{Pl}})^2$倍であることが分かる（$H$はインフレーション中の膨張率）．一度重力子モードが地平線内に入ると，そのエネルギー密度は他の相対論的粒子と同様に$R^{-4}$で減少する．簡単のため$g_*$が一定と仮定すると，$\rho_R$も$R^{-4}$で減少するので，$(k\,d\rho_{\text{graviton}}/dk)/\rho_R$は一定に保たれる．宇宙が放射優勢の間に地平線内に入るモード（$10^{-7}\,\text{Mpc} \lesssim \lambda \lesssim 13h^{-2}\,\text{Mpc}$）では，$\rho_{\text{HOR}} \simeq \rho_R$となるので， \begin{align} \frac{k}{\rho_R}\frac{d\rho_{\text{graviton}}}{dk} &\simeq \frac{4}{3\pi}\left( \frac{H}{m_{\text{Pl}}} \right)^2 = \frac{32}{9}\left( \frac{M}{m_{\text{Pl}}} \right)^4 \\ \Omega_{\text{graviton}}(k) &\simeq 10^{-4}\left( \frac{M}{m_{\text{Pl}}} \right)^4 \end{align} ここで$\Omega_{\text{graviton}}(k) = (k\,d\rho_{\text{graviton}}/dk)/\rho_C$である．これらのモードに対して$\Omega_{\text{graviton}}(k)$が$k$に依存しないことが，図の平坦部を説明している．

特に興味深い重力子モードは，現在の宇宙の地平線スケール，すなわち約3000 Mpcのスケールでちょうど地平線を横切るモードである．このモードは現在の地平線スケールでの四重極的な計量摂動に対応し，その結果，CMBR（宇宙マイクロ波背景放射）に四重極異方性をもたらす．その振幅は $(\Delta h)_k \simeq H/ m_{\text{Pl}}$ で与えられる．この事実と現在観測されているCMBRの等方性レベルから，インフレーション期のHubble定数は $10^{-4} m_{\text{Pl}}$ より小さくなければならず，インフレーションに対応する真空エネルギーも $10^{-8} m_{\text{Pl}}^4$ より小さくなければならない，ということが分かる．すなわち，インフレーションのエネルギースケールはプランクスケールよりもはるかに低い必要がある[26]．

他の非常に軽い場のde Sitter位相での励起も，興味深い粒子生成をもたらす可能性がある．例えば，アクシオン場や，場合によっては光子場などである．光子場の場合，de Sitter空間で生成された揺らぎが最終的に大規模な原始磁場の生成につながる可能性がある．この可能性は特に興味深い．なぜなら，今日観測される普遍的な天体磁場の「種」となる原始磁場の起源は，いまだ未解決の謎だからである．

特定のインフレーションモデル

ここまででインフレーションの力学を一般的に議論してきた．ここからは，具体的なモデル，すなわちスカラーポテンシャルの具体例や，それを動機づける素粒子理論について述べる．最初に断っておくが，「標準的な」インフレーションモデルは存在せず，実のところ完全に満足できるモデルもない．しかし，インフレーションを議論する枠組みとして非常に単純なモデルがいくつか存在する．これは，統一ゲージ理論を議論する際に今では廃れた$SU(5)$モデルが単純な例として用いられるのと同様である．

宇宙無毛定理

インフレーションが宇宙論的に魅力的なのは，現在の宇宙の状態が，我々の現在のHubble体積よりはるかに大きな領域において，宇宙の初期状態に対してほとんど依存しなくなる可能性を与えるからである．この事実を踏まえると，これまでインフレーションを平坦なFRW宇宙モデルの枠組みで議論してきたことは，非常に逆説的に思えるかもしれない．ここでインフレーションの中心的な問題，すなわち「インフレーションは非常に一般的な初期条件から始まり，初期データのジレンマを解決できるのか？」という問いに取り組むことにしよう．言い換えれば，「宇宙無毛定理（cosmic no-hair theorem）」は成り立つのか？という問題である．このような定理の完全な証明は存在しない（実際，インフレーションが始まる前に再崩壊してしまう閉じたFRWモデルのような単純な反例も存在する）が，この考え方には十分な動機付けがあり，インフレーションの力学をFRWモデルで扱うことが正当化されることを以下で示す．

インフレーション理論の検証

実験と観測は，あらゆる理論的推論の最終的な裁定者である．どんな理論も，その究極の栄誉は実験や観測によって最終的に検証されることである．インフレーション理論も例外ではない．これまで初期宇宙論における数少ない汚点の一つは，非常に興味深い多くの理論的推論について，実験的・観測的な検証がほとんど存在しないことであった．しかしインフレーションは，初期宇宙理論の中でも急速に検証可能になりつつある分野である．

インフレーションモデルの要約

過去数十年にわたり，Hoyle，Gold，Bondi，佐藤勝彦，Gliner，Starobinskii，Kazanas など多くの宇宙論研究者が，指数関数的膨張（インフレーション）時代の非常に興味深い宇宙論的側面を認識し，強調してきた．しかし，インフレーションが標準宇宙論の問題点をどのように解決しうるかを明確に示し，「世界に衝撃を与えた」のは Guth の1981年の論文であった．スローロール（あるいは新しい）インフレーションのアイデアによって，Guth の着想は実現可能な初期宇宙シナリオとなった．今日，インフレーションは，非常に弱く結合したスカラー場が，そのポテンシャルの極小値からずれていた初期（ただしPlanck時代以降）の宇宙で動的に進化するという宇宙論的描像となっている（図参照）．しかし，この描像には，いまだ「標準モデル」と呼べる具体的な実装が存在しない．この点は，素粒子物理学の標準模型をはるかに超える高エネルギースケールでの物理に関する我々の理解が，いまだ極めて不完全であることを考えれば，当然とも言えるだろう．

インフレーションは当初，宇宙論的な対称性の破れを伴う相転移と結びつけられていたが，現在では必ずしもそうである必要はないことが広く認識されている．それでも，この関連付けは依然として最も魅力的なインフレーションの実現形態の一つである．インフレーションは標準宇宙論の純粋に宇宙論的な難問をすべて解決する可能性を持つが，宇宙定数の謎そのものには答えていない．さらに，この謎はインフレーション理論にとってアキレス腱となりうる．もし，真空エネルギーを常に無効化するような大原理が発見された場合，インフレーションはその根本的な駆動力を失うことになる．

インフレーションが宇宙論にもたらす意味は多岐にわたる．例えば，インフレーションは，宇宙が単純な断熱的外挿から予想されるよりもはるかに巨大であることを示唆している．さらに，私たちが今日目にするすべては，「無」から，すなわち偽の真空エネルギーの形で生じたものである．私たちの身近な領域やそのはるか彼方に至るまで，インフレーションが起こったならば滑らかで平坦であるはずだが，宇宙全体の最大スケールでは非常に不規則であり，時期を異にしてインフレーションが起こった領域や，まったくインフレーションが起こらなかった領域が存在する可能性もある．さらに，異なるインフレーション領域で進化する「宇宙」は，互いに全く異なるものとなりうる．例えば，バリオン生成に必要なC，CPの破れが自発的対称性の破れ（SSB）によるものであれば，異なる領域でバリオン非対称性の符号が異なり，結果として宇宙全体ではバリオン対称となるだろう．加えて，いくつかの統一理論（特に超対称理論や超弦理論）は，多数の縮退した真空状態の存在という問題を抱えている．インフレーションは，なぜ我々の真空が$SU(3)_C \otimes SU(2)_L \otimes U(1)_Y$であるのかという謎を解く手がかりとなりうる．すなわち，異なるインフレーション領域ごとに異なる真空状態が実現されるからである[44]．もしインフレーションが宇宙初期の歴史の一部であったなら，宇宙の大域的構造は実に多様で豊かなものとなる可能性が高い．

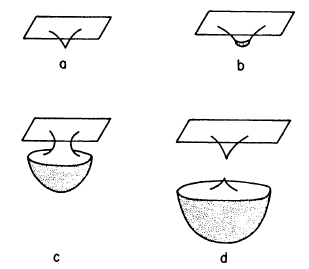
いくつかの研究者は，空の宇宙における孤立した偽の真空の球状領域の時空進化について検討している ．この問題はパラドックスを提起する．バブル内部の観測者は，偽の真空エネルギー密度によってバブルが指数関数的に成長すると予想する一方，バブル外部の観測者は，内部の圧力が負で外部の圧力がゼロであるため，バブルが収縮すると予想する．解決は非常に興味深い．偽の真空領域がある臨界サイズより大きい場合，空間のバブル状領域は指数関数的に膨張するが，空の時空にいる観測者から見ると，それはブラックホールへと崩壊し，因果的に切り離される（図参照）．さらに，Guthとその共同研究者たちは，今日の実験室で追加のインフレーション・バブルを生成する問題についても検討しており，これは古典的には禁じられているが，量子力学的トンネル効果によって起こりうることを示している．

LindeとStarobinskiiは，インフレーション中の量子力学的揺らぎの効果をさらに探究し，インフレーションバブルの中にさらにバブルが生じること，そして量子揺らぎの役割により，宇宙の物理的体積のほとんどが常にインフレーションし続けることを示した．この背後にある物理的メカニズムは単純である．もしHubble時間内の$\phi$の量子的変化（$\Delta\phi_{\text{QM}} \sim H/2\pi$）が，古典的変化（$\Delta\phi_{\text{cl}} \sim V'/3H^2$）より大きければ，$\phi$はポテンシャルを下るのと同じくらい上る可能性があり，したがって一部の領域では$\phi$がポテンシャルを上昇し，インフレーションが長引くことになる．この条件$\Delta\phi_{\text{QM}} > \Delta\phi_{\text{cl}}$は，Lindeのカオス的インフレーションモデルでは$\phi_i \gtrsim \lambda^{-1/6} m_{\text{Pl}} \sim 300\, m_{\text{Pl}}$の場合に満たされる．

インフレーション宇宙論には未解決の問題が多く残されており，特にインフレーション理論と宇宙論的観測との整合性が大きな課題となっている．他にも，以下のような重要な問題が存在する．

• インフラトンは何者か？インフラトン場はより大きな理論体系の中でどのような役割を果たすのか？インフラトンがGUTの自発的対称性の破れ（SSB）や超対称性の破れを担うモデル，インフラトンが余剰次元のコンパクト化に関係するモデル，インフラトンがプレオン的フェルミオン場から構成される複合場であるモデル，高次導関数重力理論におけるスカラー曲率と関連するモデル，あるいはLindeのモデルのように単なるスカラー場であるモデルなどが提案されている．もちろん，インフラトンがなぜこれほど弱く結合しているのかという問題も密接に関係している．これら2つの問いの答えはきっと関連しているはずである．
• 初期値$\phi_i$は何によって決まるのか？初期のインフレーションモデルでは，インフラトンの初期値は熱的な考察によって決まるとされた．しかし多くのインフレーションモデルでは，インフラトンは非常に弱く結合しているため，宇宙の熱的な粒子バスにほとんど影響されない．さらに，インフラトンがポテンシャルの極小値からずれていさえすれば，初期に熱的な粒子海が存在しようが他に何があろうが本質的に無関係である．すなわち，インフレーション前の宇宙が放射優勢である必要はない．
• インフレーションの量子力学．インフラトンの進化を半古典的に扱うことがインフレーション中は非常によく正当化されることを示したが，初期値がインフラトン場の量子力学によって決まる可能性はないのか？量子宇宙論や量子重力の何らかの側面が，インフレーションの初期条件の理解に本質的な役割を果たすのだろうか？